25339번: 반전 수와 쿼리 (acmicpc.net)
반전 수는 i < j이면서 P[i] > P[j]인 (i,j)의 개수를 말한다.
배열이 [3,2,1]이면
반전수는 (인덱스 말고) (3,2), (3,1), (2,1)로 3개가 있다.
l번, r번을 서로 교환하는 쿼리
[l,r]의 배열을 서로 뒤집는 쿼리가 주어질 때, 매 쿼리마다 수열의 반전 수를 2로 나눈 나머지를 구하는 문제
----------------------------------------------------------------------------------------------------------------------------------------------------------
배열 길이와 쿼리 수가 엄청나다보니 단순한 방법으로는 시간초과
이 문제는 핵심이 "쿼리를 수행하고 반전 수를 다 구한 다음, 2로 나누자" 이렇게 접근하면 풀기 너무 어려울 것 같다
"2로 나눈 나머지"를 구하라는 점에서 쿼리마다 정답은 0 아니면 1이다.
그러니까 매 쿼리마다 일단 반전 수의 개수를 다 구할 필요는 없다는 것
쿼리를 처리했을 때, 반전 수의 개수가 바뀌었는가? 현재 0이라면 1을 출력하면 되고, 1이라면 0을 출력
바뀌지 않았다면 현재 답을 그대로 출력하면 된다는 것
이렇게 생각한다면, 첫번째 l번과 r번을 교환하는 쿼리는...?
두 수를 단순히 교환하면 무조건 반전 수의 개수가 바뀐다. 직관적으로 너무 당연하다.
[1,2,3,4,5]에서 2와 4를 바꾸면 [1,4,2,3,5]로 바뀌니까...
어딘가가 증가상태였다면, 감소상태로, 어딘가가 감소상태였다면 증가상태로 바뀐다는 것
반전수의 개수가 증가하냐, 감소하냐는 의미가 없다. 그냥 개수가 바뀌면 0에서 1을 출력, 1에서 0을 출력
바뀌지 않으면 그대로 출력
--------------------------------------------------------------------------------------------------------------------------------
수학적으로는 다음과 같이 증명된다.
먼저 인접한 두 수를 교환한다고 해보자.
i번과 i+1번을 교환한다고 하면 P[i] < P[i+1]이면 바꿨을 때 P[i] > P[i+1]이 될 것이므로 반전수가 1 증가할 것이고
P[i] > P[i+1]이면 바꿨을 때 P[i] < P[i+1]이 될 것이므로 반전수가 1 감소할 것이다.
즉 인접한 수를 1번 교환하면, 반전 수의 개수를 2로 나눈 나머지는 항상 원래 0이면 1로 되고 1이면 0으로 된다.
l번과 r번을 교환한다고 해보자.
이것은 사실 l번 수를 l+1번과 교환하고, l+1번 수를 l+2번과 교환하고 .... r-1번 수를 r번과 교환한 다음,
r-1번 수를 r-2번 수와 교환하고 r-2번 수를 r-3번 수와 교환하고... l+1번 수를 l번 수와 교환하는 과정과 같다.
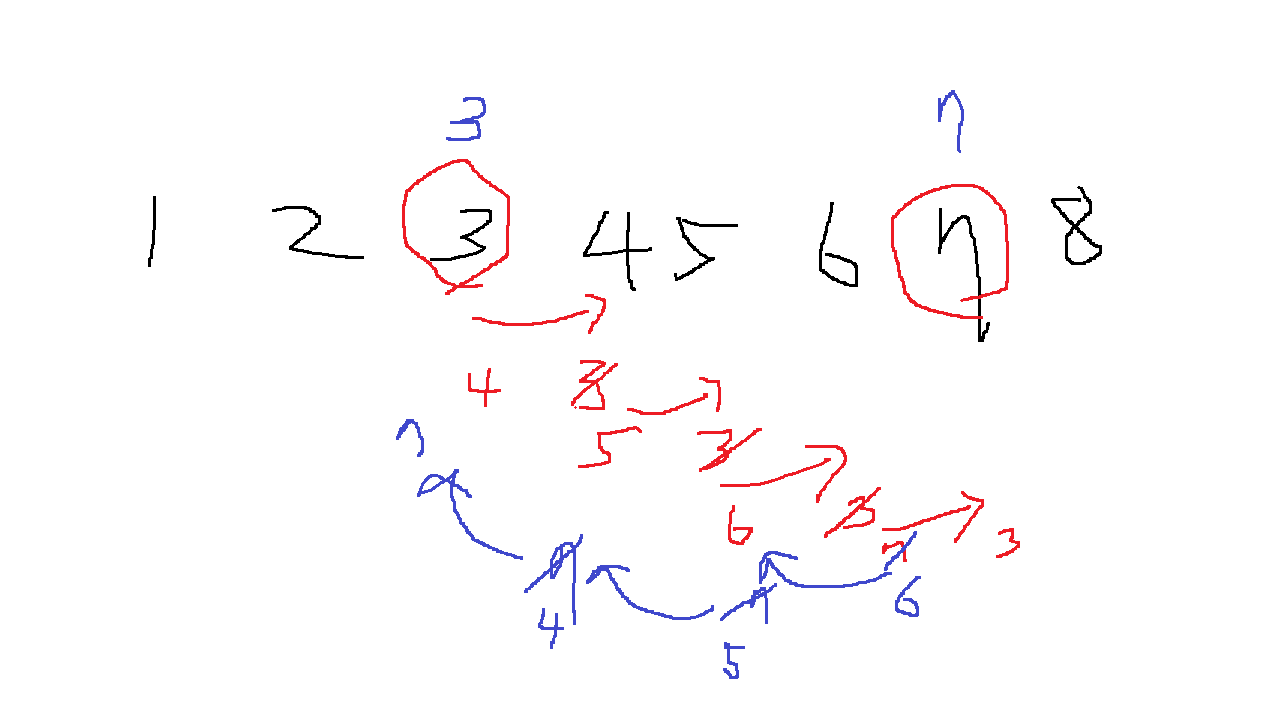
l번을 r번으로 옮기는 과정을 r - l번 수행하고, r-1번을 l번으로 옮기는 과정을 r-1-l번 수행하므로,
l번과 r번을 교환하는 과정은 서로 인접한 수를 교환하는 과정을 2(r-l)-1번 수행한다.
즉, 항상 서로 인접한 수를 교환하는 과정을 홀수번 수행하게 된다.
그러므로 원래 0에서 시작했을 때
인접한 수를 교환하면 0 > 1 > 0 > 1 > 0 > 1 > .... 이렇게 바뀌는데
짝수번이면 원래 0과 똑같아지고 홀수번이면 0에서 1로 바뀐다.
다음 [l,r]의 배열을 뒤집는 과정은...
1. P[l]과 P[r]을 서로 교환한다.
2. P[l+1]과 P[r-1]을 서로 교환한다.
3. P[l+2]와 P[r-2]를 서로 교환한다.
....
즉, l번과 r번을 서로 바꾸는 과정을 (r-l+1)//2번 수행하게 된다.
길이가 5이면 [1,2,3,4,5]에서 1,5를 바꾼다, 2,4를 바꾼다해서 5//2 = 2번
길이가 6이면 [1,2,3,4,5,6]에서 1,6을 바꾼다, 2,5를 바꾼다, 3,4를 바꾼다해서 6//2 = 3번
이때 l번과 r번을 바꾸는 과정은 1번 하면 반전 수를 2로 나눈 나머지가 바뀌므로
만약 l번과 r번을 바꾸는 과정을 (r-l+1)//2번 했을 때 그 횟수가 홀수이면 반전 수를 2로 나눈 나머지가 바뀔 것이고
짝수이면 반전 수를 2로 나눈 나머지가 바뀌지 않을 것이다.
from sys import stdin
n,q = map(int,stdin.readline().split())
c = 0
for _ in range(q):
a,l,r = map(int,stdin.readline().split())
if a == 1: #l번과 r번을 서로 바꾸면 반드시 반전수를 2로 나눈 나머지가 바뀐다
if c == 0:
c = 1
else:
c = 0
else:
#[l,r]을 뒤집는 과정은
#i번 j번을 서로 바꾸는 과정을 (r-l+1)//2번 한 것이다.
ex = (r-l+1)//2
#i번, j번을 서로 바꾸는 과정을 1번 하면 반전수를 2로 나눈 나머지가 바뀐다.
#따라서 짝수번 하면 그대로이고 홀수번 하면 바뀐다.
if ex % 2 == 1:
if c == 0:
c = 1
else:
c = 0
print(c)
-------------------------------------------------------------------------------------------------------------------------------------------------------------
반전 수의 개수가 k인 길이 n의 순열을 찾는 문제
위와 비슷한 원리를 적용해서 풀수 있다
예를 들어 길이 5이면서 반전 수의 개수가 4개인 순열을 찾고 싶다면?
[1,2,3,4,5]부터 시작하고,
1,2를 교환하면 [2,1,3,4,5]로 1개
1,3을 교환하면 [2,3,1,4,5]로 2개
1,4를 교환하면 [2,3,4,1,5]로 3개
1,5를 교환하면 [2,3,4,5,1]로 4개
...
이런 전략으로 0번 원소를 n-1번으로 보내고, 다시 0번 원소를 n-2번으로 보내고,...
이러면 총 n-1 + n-2 + n-3 + ... + 1 = n(n-1)/2개만큼 반전수가 증가할 수 있다.
k의 최댓값이 n(n-1)/2이므로 이 전략이 정당하다.
#반전 수가 k개인 길이 n의 순열을 찾는 방법
n,k = map(int,input().split())
#[1,2,3,4,..,n]에서 시작해서
#0번 원소를 맨 뒤로 보내면 n-1,n-2,n-3,...개씩 증가하므로...
#이 작업을 몇번 해야하는지 구한다
A = list(range(1,n+1))
i = 1
while k > n-i:
k -= (n-i)
i += 1
#i = 3으로 나오면?
#0번 > n-1
#1번 > n-2로 보내는 작업을 할 수 있다는 뜻
#[1,2,3,4,5,...]에서 index = 1번까지 1,2를 맨 뒤로 보내야한다는 뜻
#그렇지만 반복문 끝나면 i = 3이므로, i -= 1
i -= 1
#[1,2,3,4,5]에서 [1,2]를 뒤로 보내야한다면
#[1,2]
#[3,4,5]로 나누고
#[1,2]에서 순서대로 빼서 [3,4,5]에 넣으면 [3,4,5,2,1]이 된다
stack = A[:i]
B = A[i:]
while stack:
B.append(stack.pop())
#남은 k값 만큼 B배열에서 인접한 수끼리 왼쪽에서 차례대로 교환해주고 k를 1씩 빼준다
#k가 0이 되는 순간 해당 B배열이 정답
for i in range(n-1):
if k == 0:
break
B[i],B[i+1] = B[i+1],B[i]
k -= 1
print(*B)
처음에 k에서 n-1,n-2,n-3,...을 빼다보면 n-i를 빼야하는데 n-i를 빼면 음수가 되는 경우가 분명 있을 것이다
그러면 0번 원소를 맨 뒤로 보내는 작업을 몇번이나 해야하는지 구하고 싶다
예를 들어 길이 5이면서 반전수가 6개인 순열을 구하고 싶다면?
6 = 4 + 2이므로 0번 원소를 n-1번으로 보내는 작업을 1번하고, 2가 남는다
i = 1
while k > n-i:
k -= (n-i)
i += 1
#i = 3으로 나오면?
#0번 > n-1
#1번 > n-2로 보내는 작업을 할 수 있다는 뜻
#[1,2,3,4,5,...]에서 index = 1번까지 1,2를 맨 뒤로 보내야한다는 뜻
#그렇지만 반복문 끝나면 i = 3이므로, i -= 1
i -= 1
어떤 원소까지를 뒤로 보내야하는지 알았다면, 실제로 뒤로 보내준다
[1,2,3,4,5]에서 1,2를 뒤로 보내야한다면..?
[3,4,5,2,1] 형태가 되어야하므로....
[1,2]
[3,4,5]로 나눈다음...
[1,2]에서 맨 뒤에서부터 빼서 [3,4,5]에 순서대로 집어넣는다
stack = A[:i]
B = A[i:]
while stack:
B.append(stack.pop())
마지막 남은 k값만큼 B배열에서 인접한 수끼리 교환해나가고, k를 1씩 뺀다음 k가 0이 되면 그 배열 B가 정답
for i in range(n-1):
if k == 0:
break
B[i],B[i+1] = B[i+1],B[i]
k -= 1
print(*B)'알고리즘 > 애드 혹 알고리즘' 카테고리의 다른 글
| 모든 순서쌍의 합의 나머지를 합해야하는데 매 항마다 나머지를 더하면 안되는 문제 (0) | 2024.06.06 |
|---|---|
| n으로 나누어 떨어지면서 자릿수의 합도 n으로 나누어 떨어지는 정수 (0) | 2024.06.01 |
| 정수들이 섞여있는 수열에서 연속하는 정수 수열을 O(N)에 분리하기 (0) | 2024.05.12 |
| 무방향 연결그래프에서 정점의 성질 관찰하기 (0) | 2024.05.10 |
| ABC 351 F번 복기 - 알고리즘 문제에 max함수를 바꾸는 트릭 2가지 (0) | 2024.05.02 |

