https://atcoder.jp/contests/abc419/tasks/abc419_c
C - King's Summit
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
좌표평면 위의 n개의 점들이 1초에 팔방향으로 움직이거나 멈춰있을 수 있다.
이때, 모든 점들이 하나의 점에 모인다고 할때, 걸리는 최단 시간을 구한다면?
----------------------------------------------------------------------------------------------------------------------------------------------------------
모든 사람들이, 어떤 점 (X,Y)에 모인다고 가정해보자.
i번째 사람 $(X_{i},Y_{i})$와의 거리는?
팔방향으로 움직일 수 있기 때문에, $max(|X - X_{i}|, |Y-Y_{i}|)$와 같다.
왜냐하면 $a = |X - X_{i}|, b = |Y - Y_{i}|$라고 해보자. a나 b 둘중 작은 값이 min(a,b)라고 한다면
min(a,b)만큼 먼저 움직이고 남은 거리 max(a,b) - min(a,b)만큼 움직여야한다.
즉, max(a,b)만큼 움직이면 된다.

그러면 모든 점 i = 1,2,3,..,N에 대해 이들이 어떤 점 (X,Y)로 모이는데 걸리는 최단 시간은?
각각의 점이 (X,Y)로 모이는데 걸리는 시간 max(|X - Xi|, |Y - Yi|)만큼 이동하고 어떤 인원이 안오면 그 시간만큼 멈춰있으면 된다.
따라서 전체 걸리는 시간은...

이 값을 구하기 위해 먼저 다음이 성립함을 이해해야한다.

(좌변 >= 우변)
$R_{min} <= R_{i} <= R_{max}$이므로, $R - R_{min} >= R - R_{i} >= R - R_{max}$
따라서, $|R - R_{i}| <= max(|R - R_{min}|, |R - R_{max}|)$
예를 들어 왜냐하면 -7 <= x <= 3이면 |x| <= max(|7|,|3|)잖아
이는 모든 i에 대해 성립하므로, $max|R - R_{i}| <= max(|R - R_{min}|, |R - R_{max}|)$
(좌변 <= 우변)
먼저 $|R - R_{max}| >= |R - R_{min}|$이라고 해보자.
$max(|R - R_{max}|, |R - R_{min}|) = |R - R_{max}|$이다.
이때, $|R - R_{max}|$는 i = 1,2,3...,n에 대하여 $|R - R_{i}|$중 하나의 값이다.
따라서 모든 i에 대해 최댓값은 논리적으로 이 값 이상이여야한다.
$max |R -R_{i}| >= |R - R_{max}|$
비슷한 논리로 $max |R - R_{i}| >= |R - R_{min}|$
그러므로 $max |R -R _{i}| >= max(|R - R_{max}|, |R - R_{min}|)$
따라서, 좌변 >= 우변, 좌변 <= 우변이므로 두 값은 동치이다.
------------------------------------------------------------------------------------------------------------------------------------------------
근데 어렵게 생각할 것 없이
어떤 특정한 R에 대하여... Ri가 될 수 있는 값은 Rmin <= Ri <= Rmax이다.
이 특정한 R과 Ri 사이 거리의 최댓값은..?
직접 그려보면 Rmin과 Rmax사이 거리 중 하나가 최댓값이 된다.

수식적으로 볼려고 하니까 어려워보였지
기하학적으로 보면 직관적으로 보임
----------------------------------------------------------------------------------------------------------------------------------------

A = max ai, B = max bi라 하고, M = max(A,B)이라 하자.
ai <= A이고 bi <= B이므로, max(ai,bi) <= max(A,B) = M이다.
따라서 좌변 <= 우변이다.
반대로 M = max(A,B)는 A와 B중 더 큰 쪽이고, M = A라고 하자.
A는 어떤 인덱스 i에 대해 ai중 하나의 값이므로, 모든 i = 1,2,..,n에 대하여 max ai는 A이상이다.
max ai >= A=M이므로 좌변 >= 우변이다.
M = B여도 마찬가지다. 따라서 좌변 = 우변이다.

이제 위 식을 모든 i = 1,2,3...,n에 대해 풀어써보면
$max( max(|R - R_{1}|, |C - C_{1}|), max(|R - R_{2}|, |C - C_{2}|), ... , max(|R - R_{n}|, |C - C_{n}|) )$
각각에서 $|R - R_{i}|$와 $|C - C_{i}|$중 더 큰 값을 선택하고 그리고 n개들 중에서 더 큰 값을 선택한다.
그러면 이는 $|R - R_{i}|$중 최댓값과 $|C - C_{i}|$중 최댓값에서 더 큰 값을 고르는 것과 같을 것이다.
그러므로 두 사실을 합치면 다음이 성립한다.
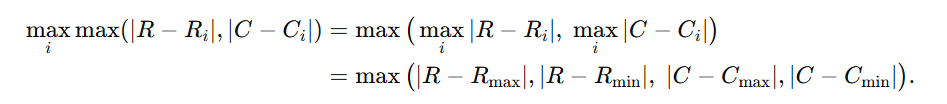
이제 문제에서 원하는 값은
사람들이 만날 수 있는 가능한 모든 R,C에 대하여 걸리는 시간

의 최솟값이다.
그리고 이는...

의 최솟값을 구하는 문제이다.
$$max(|R - R_{max}| , |R - R_{min}|, |C - C_{max}|, |C - C_{min}|)) = max( max(|R - R_{max}|,|R - R_{min}|), max(|C - C_{max}|,|C - C_{min}|))$$
이다.
$max(|R - R_{max}|, |R - R_{min}|) = A(R), max(|C - C_{max}|, |C - C_{min}|) = B(C)$라고 하자.
$$min_{R,C} max(A(R),B(C))$$를 구하는 문제이다.
이는 max( minA(R), minB(C))와 같은데...
minA(R) = a, minB(C) = b라고 하면... A(R) >= a, B(C) >= b이므로 모든 R,C에 대하여 A(R)과 B(C)중 더 큰 값을 고르고,
최솟값을 고르더라도 이는 max(a,b)보다 크거나 같다.
즉, min max(A(R),B(C)) >= max(a,b)
이제 반대로 어떤 R'과 C'에 대하여 max(A(R'), B(C')) >= min max(A(R), B(C))이다.
왜냐하면 모든 R,C의 집합에서 max(A(R),B(C))값들의 최솟값은 어떤 R,C를 골라 구한 max(A(R'),B(C'))보다 작거나 같을테니까
만약 이 R',C'이 max(a,b)와 같게되는 그러한 R',C'이라면.. 그리고 그러한 R',C'은 반드시 존재하기 때문에
max(a,b) >= min max(A(R), B(C))이다.
따라서 좌변 >= 우변, 좌변 <= 우변이므로 둘은 동치이다.
$$min_{R,C} max(A(R), B(C)) = max(min_{R} A(R), min_{C} B(C))$$
그러므로 $max(|R - R_{max}|, |R - R_{min}|)$의 R에 대한 최솟값과 $max(|C - C_{max}|, C - C_{min}|)$의 C에 대한 최솟값을 찾으면 된다.
$max(|R - R_{max}|, |R - R_{min}|)$의 최솟값은 무엇을 의미하는가?
수식적으로 보면 어려워보이지만 기하학적으로 놓고 보면 직관적으로 보인다
구간 $[R_{min}, R_{max}]$위의 한 점 R에 대하여 R에서 $R_{min}$, $R_{max}$까지 거리의 큰 값을 최소로 만드는 점 R은 어디인가?
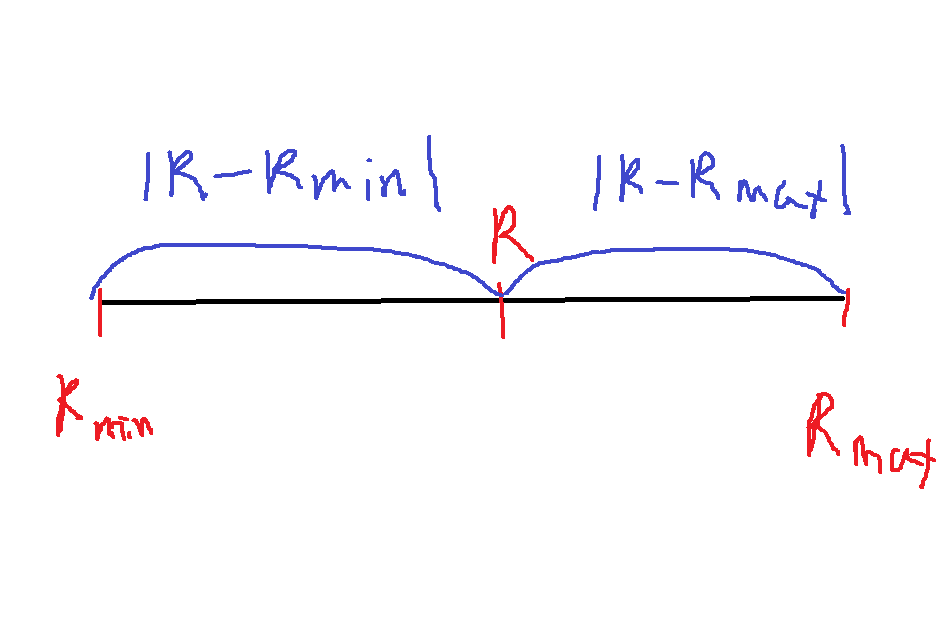
이러한 점 R은 두 점 $R_{min}, R_{max}$의 중점이다. 왜냐하면 중점에서 max쪽으로 이동하면 거리가 더 큰 min까지 거리를 취하게 되고
중점에서 min쪽으로 이동하면 거리가 더 큰 max쪽 거리를 취하게 되고,
그러다보니 두 거리가 정확히 같은 지점인 중점이 최솟값을 가지는 지점이 된다.
실수면 상관 없는데 정수만을 골라야한다면 조금 골치아프다.

위와 같이 이해할 수 있다.
따라서 구하고자 하는 거리는 (R_max - R_min)/2보다 크거나 같은 최소의 정수이다.
이는 프로그래밍에서 (R_max - R_min + 1)//2로 간단하게 구할 수 있다.
n = int(input())
R = []
C = []
for _ in range(n):
r,c = map(int,input().split())
R.append(r)
C.append(c)
R_max = max(R)
R_min = min(R)
C_max = max(C)
C_min = min(C)
R = (R_max - R_min+1)//2
C = (C_max - C_min+1)//2
print(max(R,C))
혹은 그림에서 보인 것처럼 중점 $\lfloor x \rfloor$을 구한 다음 Rmax와의 거리의 최댓값으로도 구할 수 있다
n = int(input())
R = []
C = []
for _ in range(n):
r,c = map(int,input().split())
R.append(r)
C.append(c)
R_max = max(R)
R_min = min(R)
C_max = max(C)
C_min = min(C)
R = (R_max + R_min)//2
C = (C_max + C_min)//2
print(max(R_max - R,C_max - C))
----------------------------------------------------------------------------------------------------------------------------------------------
점들이 수직선 위의 점 x1,x2,...,xn이라고 주어진다면, 이들이 한 점으로 모일때 최단시간은...

위의 문제처럼 좌표평면 위의 점 (r1,c1),...,(rn,cn)이 주어진다면.. 이들이 한 점으로 모일때 최단시간은...

3차원 위의 점이라면...

1차원 먼저 생각하고
2차원..으로 확장해나갔으면 더 쉬웠을지도
'기하학' 카테고리의 다른 글
| 벡터 (x,y)를 90도 회전하는 방법 (0) | 2024.11.16 |
|---|---|
| 평면 위 두 직사각형이 서로 겹치는 직사각형의 좌표 구하는 놀라운 방법 (0) | 2024.08.29 |
| 사각형과 원이 겹치는 영역의 좌표의 개수는 O(N)에 구할 수 있을까 (0) | 2024.08.01 |
| 원 안에 원을 가득 채우는 문제?(circle packing in a circle) (0) | 2024.07.27 |
| 꼭짓점이 둥근 볼록껍질(round convex hull)의 둘레의 길이를 구하는 법 (0) | 2023.09.27 |

