1. Backpropagation through time
RNN의 backpropagation 알고리즘

모든 token을 계산하면서 ground truth와 비교하면서 loss를 최소화하는 방향으로 backpropagation을 통해 gradient를 계산
그런데 수백, 수천만 길이의 sequence면 한정된 GPU에서 계산이 불가
2. Truncated backpropagation through time
그러니까 일부 time을 잘라가지고 만든 여러개의 truncation을 만든다.
그래서 제한된 sequence를 가지는 truncation에서 backpropagation을 진행하고 다음 truncation에서도 진행하고 과정을 반복한다
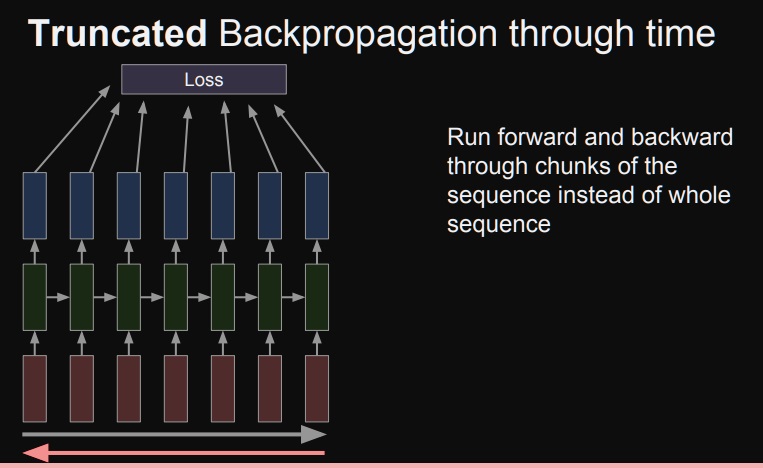
자른 구간에서는 이제 GPU가 허용하는 한에서 backpropagation이 가능
이 truncation에서 RNN모듈의 가중치들이 학습이 된다.
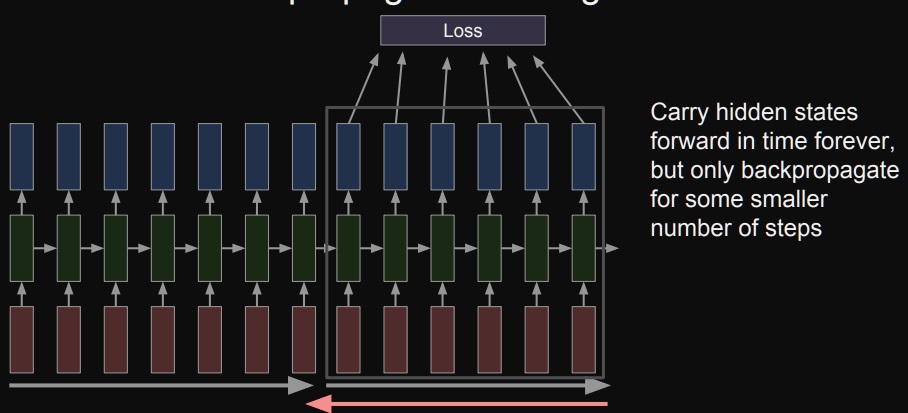
그러면 이제 다음 truncation에 존재하는 부분만 backpropagation으로 학습을 진행하여 가중치를 갱신한다
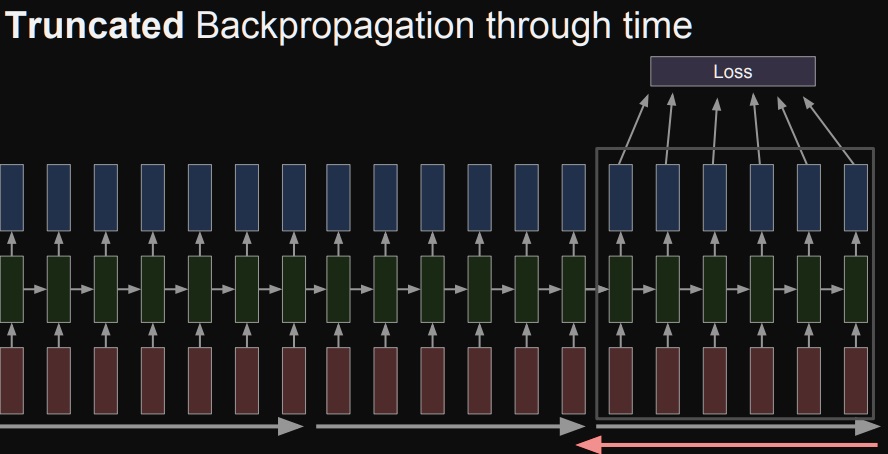
마지막으로 남은 구간에서 backpropagation을 진행하여 가중치를 갱신한다
근데 이제 조금만 생각해보면 알겠지만 truncation 단위로 학습을 진행하면 3개의 truncation 각각의 가중치가 다를수 있다는 문제를 생각해볼 수 있다.
그런데 RNN은 가중치를 공유하는 네트워크인데 각각 다르다는게 조금 아쉽다
3. 예시로 이해하는 RNN의 학습
RNN이 학습하면서 정보를 저장하는 공간은 매 time step마다 update를 수행하는 hidden state vector
hidden state vector에는 예를 들어 :으로 끝나면 한줄 띄어라, 이곳에서는 공백을 2번 사용해라 등등이 저장
그래서 hidden vector의 어떠한 차원에 정보가 저장되어있는지 확인하고자 하나의 차원을 고정하고 시간이 흐르면서 어떻게 바뀌는지 분석했다.
3-1) quote detection cell
어떤 hidden vector의 cell에서 계산된 값을 보니 다음과 같은 패턴
어떤 cell에서는 quote가 어디서 열리고 닫혀야하는지를 인식하고 있음

3-2) if statement cell
어떤 cell은 if문을 어디에 써야하는지 인식하고 있다는 것을 알수 있다.

4. gradient vanishing/exploding problem
최종 예측이 잘 수행 되려면 가장 먼 거리의 정보도 최종 시점으로 잘 전달되어야 가능하다.
그러나 RNN은 가중치가 반복적으로 곱해진다는 사실에서 backpropagation을 할때 가중치의 곱이 1보다 크면 gradient가 폭발적으로 증가할 것
가중치의 곱이 1보다 작으면 gradient가 계속 감소하여 소멸될 것이다.
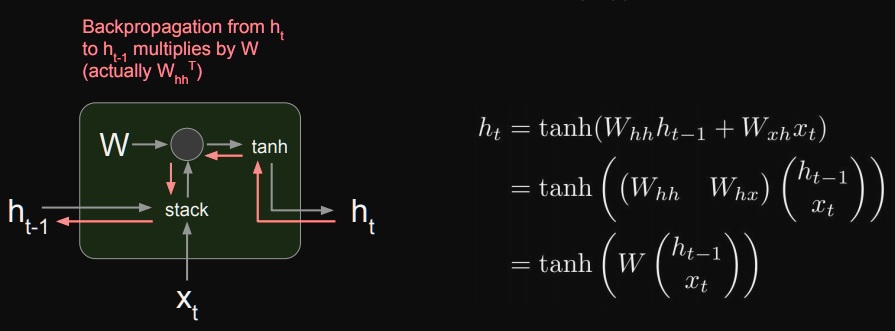
위에서 주어진 식으로부터 $h_{t-1}, h_{t-2}, ... $를 반복적으로 구하여 대입해보면

위와 같이 반복적으로 $W_{hh}$가 곱해질 것이며 $h_{t}$로 실제 값을 예측하니까 $W_{hh}$에 의한 미분을 수행
여전히 $W_{hh}$의 반복적인 곱이 남아있어서 gradient가 폭발적으로 증가하거나 gradient가 폭발적으로 소멸하거나
결국 gradient가 먼 거리까지 잘 흐르지 않는 현상 발생

RNN과 LSTM이 얼마나 gradient가 빠르게 감소하는지 비교

RNN이 gradient가 빠르게 소멸하여 학습이 안되는 동안에 LSTM은 여전히 학습이 진행되고 있다는 점이 중요하다.
LSTM은 RNN의 gradient vanishing을 개선한것일뿐 완전히 해결한것은 아니다.
LSTM도 gradient vanishing은 언젠가는 일어날 수 있다.
'딥러닝 > NLP' 카테고리의 다른 글
| text-to-text format 방법론 간단하게 (0) | 2024.04.04 |
|---|---|
| RNN을 개선한 LSTM(Long short term memory) (0) | 2023.07.27 |
| RNN의 여러가지 유형(one to one, one to many, many to one, many to many) 되돌아보기 (0) | 2023.07.11 |
| Vanilla RNN에서 hidden vector로 예측값을 만드는 과정 (0) | 2023.07.11 |
| word embedding을 하는 또 다른 모델 Glove의 아이디어 (0) | 2023.07.05 |

