hidden vector의 차원은 hyperparameter이다. 여기서는 2차원이라고 가정해보자.
3차원의 입력벡터 $X_{t}$가 들어가고 2차원의 hidden state vector인 $h_{t-1}$이 RNN의 입력으로 들어간다고 해보자.
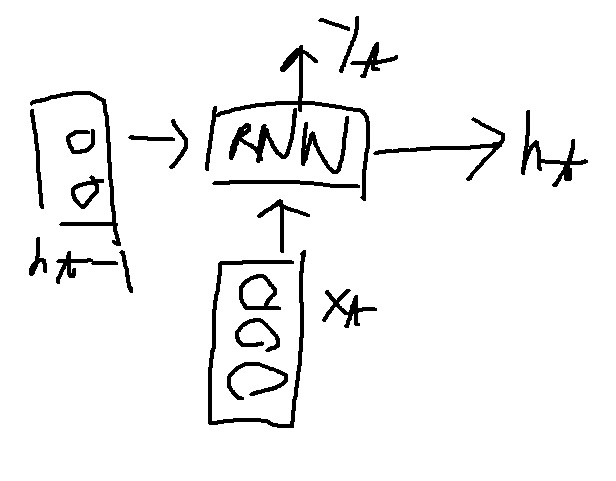
처음에는 $X_{t}$와 $h_{t-1}$이 concatenation되어 hidden layer에 fully connected 된다.
당연하지만 $h_{t-1}$이 2차원이기때문에 $h_{t}$를 뽑아내는 layer의 차원도 2차원이다.
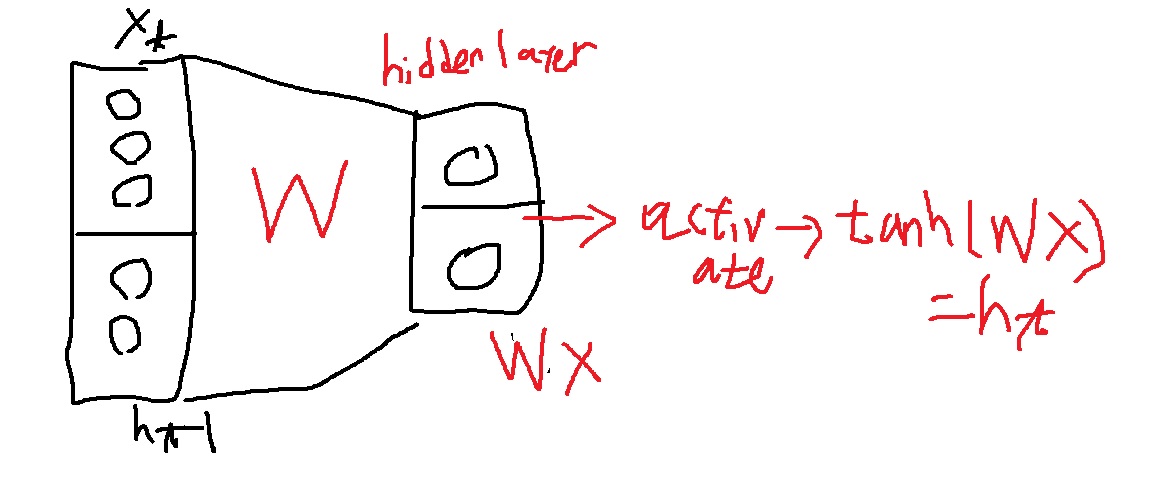
hidden layer의 선형변환 W와 입력벡터의 곱 WX에 nonlinear activation인 tanh(WX)로 $h_{t}$가 뽑힌다.
Vanilla RNN이 실제로 tanh()를 activate function으로 썼다고 한다.
hidden layer의 계산을 조금 더 자세히 살펴본다면
5*1벡터가 입력으로 들어가 2*1벡터를 뽑아내므로 W의 차원이 2*5가 되어야 WX가 2*1이 된다.

A와 $X_{t}$의 내적에 B와 $h_{t-1}$의 내적의 합으로 선형변환의 첫번째 성분이 구해지고
비슷한 방식으로 C와 $X_{t}$의 내적에 D와 $h_{t-1}$의 내적의 합으로 두번째 성분이 구해진다.
바꿔말하면 A,C는 $X_{t}$를 바꾸고 B,D는 $h_{t-1}$을 바꾼다.
그래서 A와 C의 합을 $W_{xh}$라 하고 B와 D의 합을 $W_{hh}$라고 표시하여
선형변환의 결과는 $WX = W_{xh}X_{t} + W_{hh}h_{t-1}$라고 표시할 수 있다.
$W_{xh}$는 $X_{t}$를 $h_{t}$로 바꾼다는 의미에서 쓴 것이고
$W_{hh}$는 $h_{t-1}$을 $h_{t}$로 바꾼다는 의미에서 notation을 쓴 것이다.
선형변환 결과의 activation function인 tanh를 취한 값이 RNN의 hidden state vector $h_{t} = tanh(W_{xh}X_{t} + W_{hh}h_{t-1})$가 된다.
저번에 배운 projection layer에 이어 hidden layer의 의미로 활성화함수를 써야 의미가 있다. 잊어서는 안된다.
다시 강조하지만 $h_{t}$는 RNN의 최종 예측값이 아니다.
이것으로 task의 예측을 수행하고자 할 때 output layer에 이 값을 보내 선형변환 시켜 예측을 수행하는 것이다.
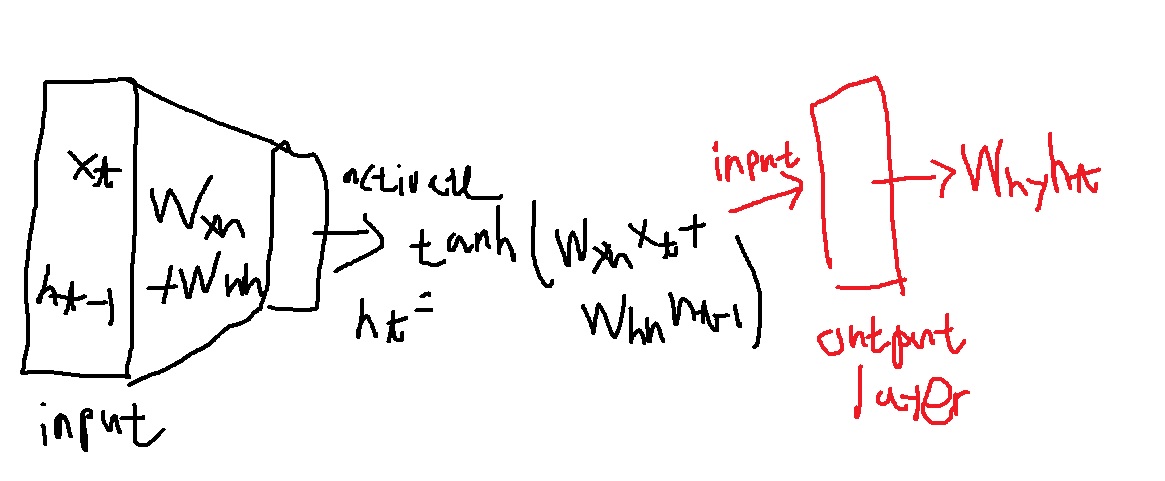
$h_{t}$에 선형변환 $W_{hy}$를 곱하여 y로 변화시킨다. 그런 의미에서 $W_{hy}$라는 notation을 쓴 것이다.
output layer의 결과로 나온 $W_{hy}h_{t}$에 대해 classification을 수행하고 싶다면
softmax(multi-label)나 sigmoid(binary label)를 취하여 확률벡터로 해석하게 할 수 있다.
--------------------------------------------------------------------------------------------------------------------------
****softmax가 layer의 활성화함수가 아닌 이유
예전에 했지만 softmax가 layer의 활성화함수로 안볼수 있는 것이 softmax는 취하지 않아도 비례하는 증가함수라서
$W_{hy}h_{t}$에서 최댓값이 one hot vector의 1이 된다는 사실을 기억, 단순히 확률해석을 위해서 사용하는 느낌이 크다.
--------------------------------------------------------------------------------------------------------------------------

$y_{t}$는 RNN의 현 step에서 task 예측값
$softmax(W_{hy}h_{t})$나 $W_{hy}h_{t}$에서 one hot vector로 만든 것이 $y_{t}$일수도 있지만
때로는 선형변환한 결과만 사용할 수도 있으니 <그런 task는 얼마든지 있다>
$y_{t} = W_{hy}h_{t}$일 수도 있다.
'딥러닝 > NLP' 카테고리의 다른 글
| RNN의 특별한 학습방법 Backpropagation through time 이해해보기 (0) | 2023.07.12 |
|---|---|
| RNN의 여러가지 유형(one to one, one to many, many to one, many to many) 되돌아보기 (0) | 2023.07.11 |
| word embedding을 하는 또 다른 모델 Glove의 아이디어 (0) | 2023.07.05 |
| NLP에서 language model의 역사 훑어보기 (0) | 2023.05.08 |
| text data를 다루는 NLP + computer vision과의 활용 - image captioning 기본 배우기1 (0) | 2023.02.27 |

