1. 문제
14860번: GCD 곱
N과 M 이 주어졌을 때, GCD(1, 1) × GCD(1, 2) × ... × GCD(1, M) × GCD(2, 1) × GCD(2, 2) × ... × GCD(2, M) × ... × GCD(N, 1) × GCD(N, 2) × ... × GCD(N, M)을 구하는 프로그램을 작성하시오.
www.acmicpc.net
2. 풀이
N*M 테이블에서 최대공약수를 구해본다.
예를 들어 N = 10, M = 10이라고 한다면..
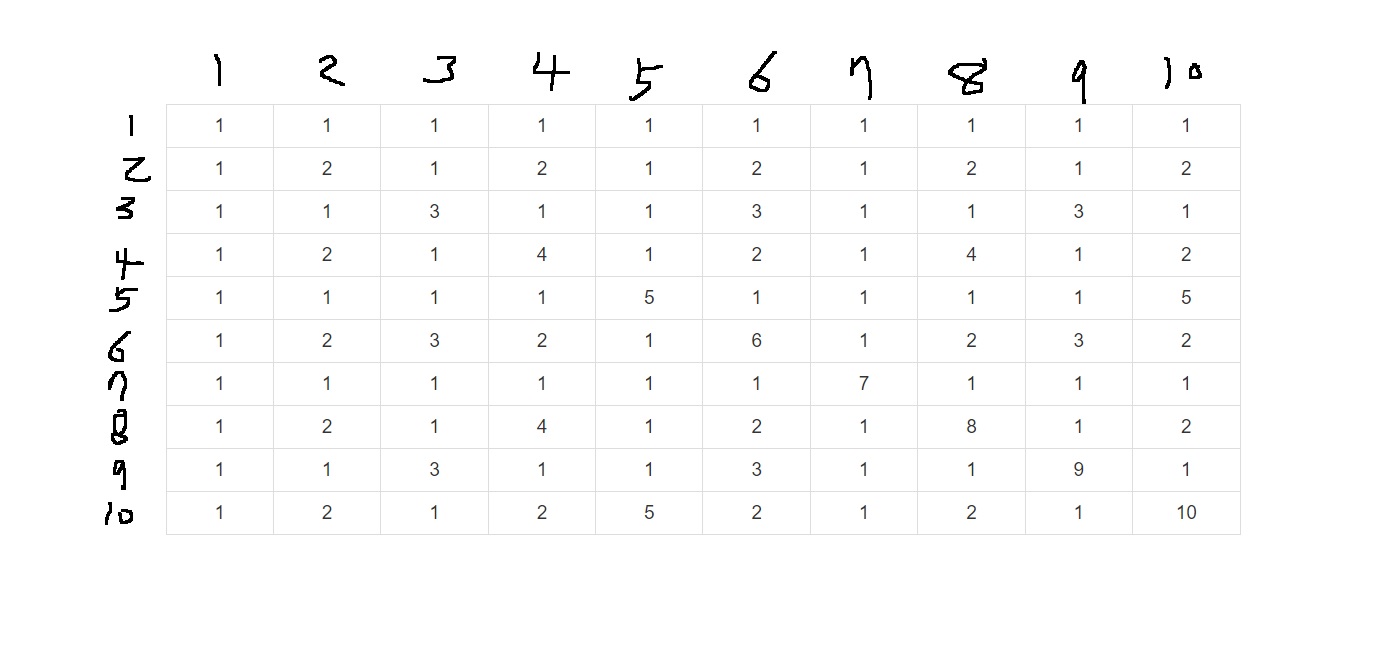
1은 곱해봤자 의미없으니까 2부터 테이블에 몇개나 나타나는지 한번 찾아보면
5*5 = 25개 있다는 것을 알 수 있는데
이는 행과 열에서 2의 배수가 몇개나 있는지를 세면 된다는 것을 볼 수 있다.
길이 10인 행에는 2의 배수가 5개 있고 길이 10인 열에는 2의 배수가 5개 있거든
일반적으로 i의 개수는 n//i * m//i개가 있게 된다.
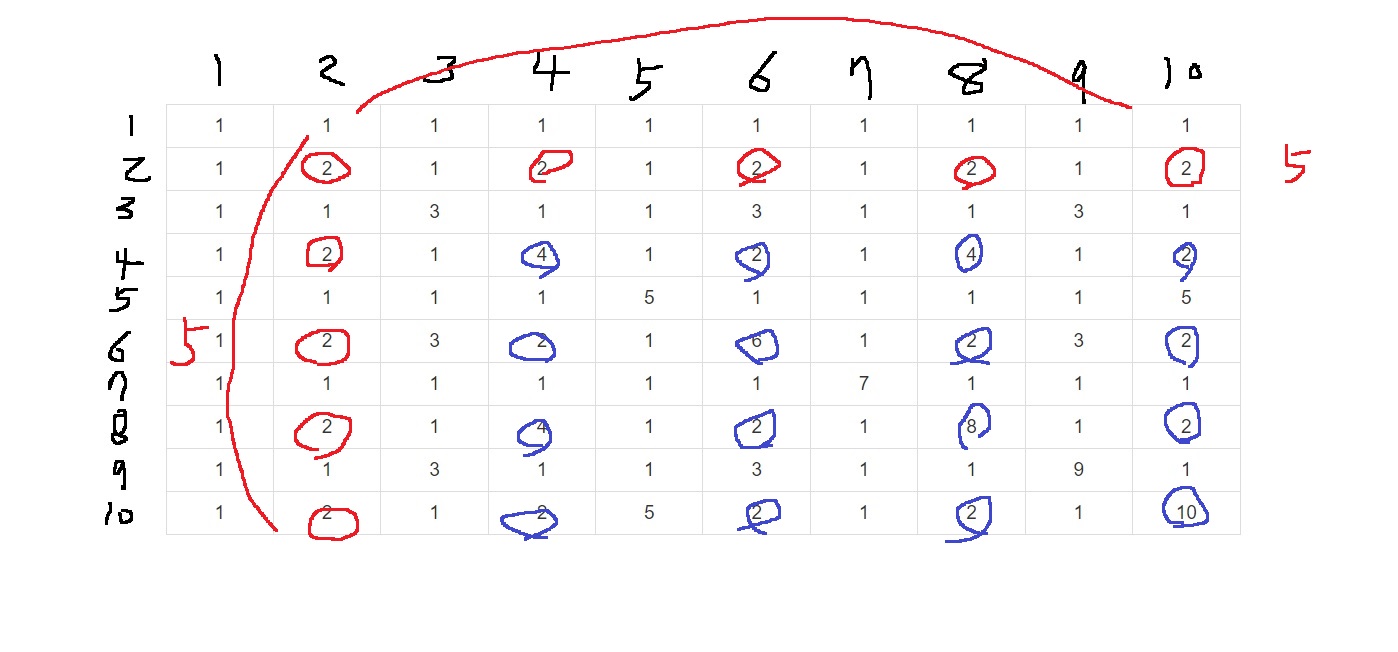
근데 4나 6 8 10도 2를 소인수로 가지는데 어차피 곱해질거니까 얘도 같이 세어줘야함
그러니까 2의 개수가 25개로 끝이 아니라 2의 제곱인 4에는 2가 두번 들어가 있거든
4의 개수가 몇개인지를 세어본다면 위의 규칙대로 n//4 * m//4인것을 알 수 있는데
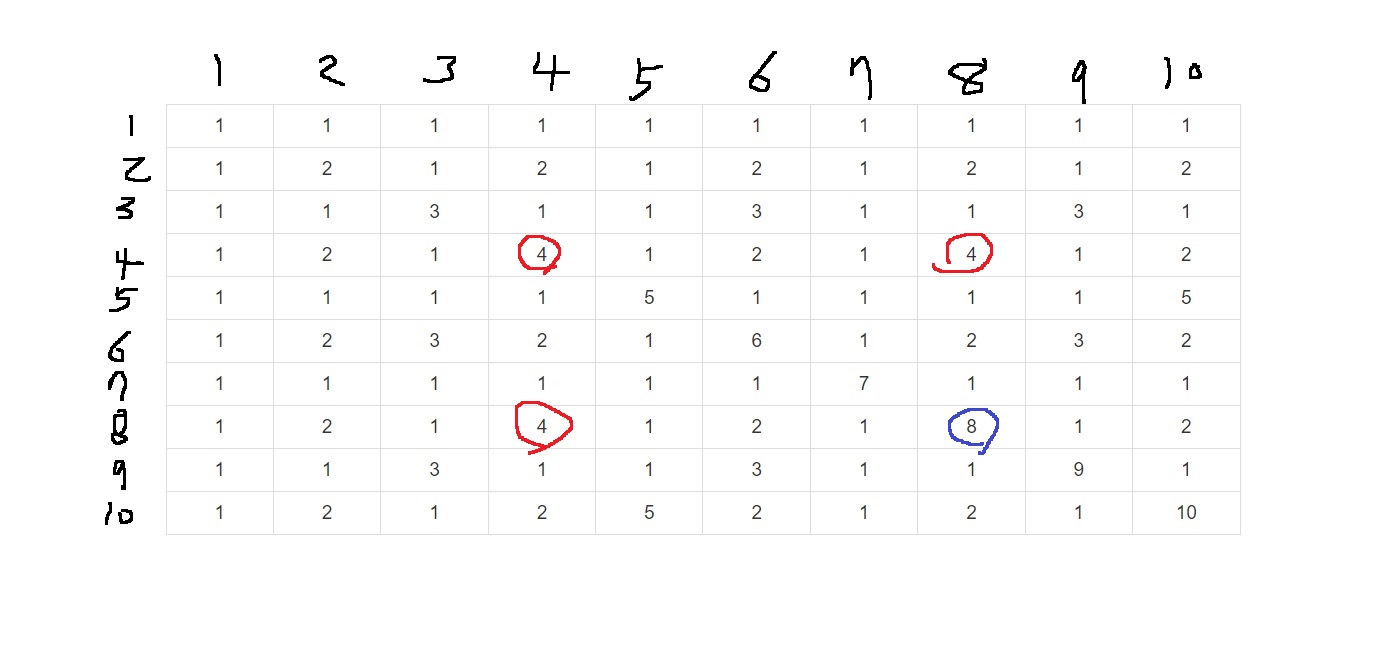
4가 10//4 * 10//4 = 2*2 = 4개있으니까... 그런데 4는 2가 2번 곱해지니까 2는 총 8개 존재하는데...
근데 위에서 2의 개수 25개를 세면서 이미 1번 셌으니까 2의 개수는 4개만 세주면 된다
마찬가지로 8에 2가 3번 있으니까 8의 개수도 세어야 2의 개수를 완벽하게 셀 수 있는건데
8의 개수는 10//8 * 10//8 = 1*1 = 1개 있을것이다.
그런데 8은 2가 3번 들어가 있으니까 2가 3개 존재하는건데..
2의 개수 25개에 4의 개수 8개( = 2는 4개)에 2번 세어졌으니까 3에서 2를 빼서 8의 개수인 1개만 더해주면 된다.
그러니까 2의 총 개수는...
2의 개수 + 4의 개수 + 8의 개수 = 25 + 4 + 1 = 30

이번엔 3의 개수를 세어볼까?
굳이 안세봐도 10//3 * 10//3 = 9개인것은 예상할 수 있는데

마찬가지로 3의 거듭제곱인 9에도 3이 2개나 있으니까.. 모든 3의 개수를 셀려면 9의 개수도 필요하다.
9의 개수는 10//9 * 10//9 = 1개 있는데... 9에는 3이 2개 있으니까... 3을 2개 세어야하나?
하지만 위 그림에서 3의 개수 9개를 세면서.. 9도 세었으니 1번만 세어주면 된다.
즉 3의 총 개수는...
3의 개수 + 9의 개수 = 9 + 1 = 10개
이번에는 4의 개수를 세어볼까?
그런데 4의 개수는 2의 개수를 세면서 다 세었다..
그러면 5의 개수를 세어볼까?
10//5 * 10//5 = 2*2 = 4개 있을거라고 예상할 수 있다
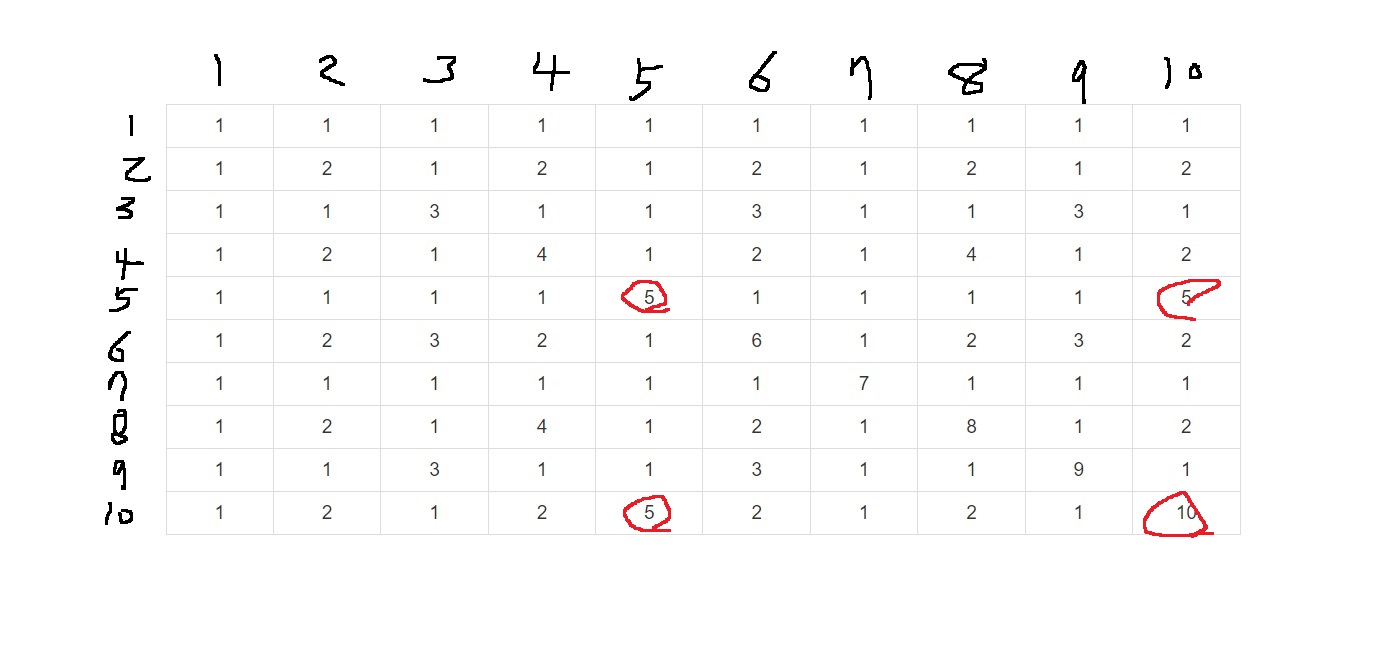
5의 총 개수를 셀려면 5의 거듭제곱인 25도 세어야겠지만.. 10 이내에 25가 존재하지는 않는다
이번엔 6의 개수를 세어볼까?
10//6 * 10//6 = 1*1 = 1개가 있는데 이 친구는 정말 흥미로운게
전체에 6을 곱하는 것은 사실 2를 곱하고 3을 곱하는것과 마찬가지다.
2의 개수와 3의 개수를 세면서, 이미 세었다
2의 개수 30개와 3의 개수 10개를 모두 곱하면서 6은 곱해지는거나 마찬가지다.

7도 10//7 * 10//7 = 1개 있고, 8은 2의 개수를 세면서 셌고, 9도 3의 개수를 세면서 셌으며...
10 = 2*5인데 2의 개수와 5의 개수를 세면서 이미 포함된거를 알 수 있다.
---------------------------------------------------------------------------------------------------------------------------------------------------
종합하면 다음과 같다.
n*m 테이블에 최대공약수 gcd(i,j)를 써넣고 모든 최대공약수의 곱을 구할려면...
1) 자연수 p의 개수가 n//p * m//p만큼 존재한다.
2) 소수 p의 개수를 세서 p를 그 개수만큼 거듭제곱하면 된다.
3) 소수 p의 총 개수는 p의 개수 + $p^{2}$의 개수 + $p^{3}$의 개수 + .....
4) 서로 다른 소수 pq의 곱으로 이루어진 합성수의 개수는 위에서 소수를 세면서 다 세지니까 셀 필요 없다.
--------------------------------------------------------------------------------------------------------------------------------------------------------
알고리즘은 다음과 같다.
1) n과 m중 작은 값을 n이라 한다.
2) 에라토스테네스의 체로 n이하의 모든 소수를 찾는다.
3) 소수 리스트에서 모든 소수 p를 순회해서, p의 개수 + $p^{2}$의 개수 + ... 를 구한다.
4) modulo exponentiation을 이용해서 빠르게 그 개수만큼 p의 거듭제곱을 누적해준다.
def get_prime(n):
result = [1]*(n+1)
for i in range(2,int((n+1)**(1/2))+1):
if result[i] == 1:
for j in range(i*i,n+1,i):
result[j] = 0
return [i for i in range(2,n+1) if result[i] == 1]
n,m = map(int,input().split())
if n > m:
n,m = m,n
prime_list = get_prime(n)
answer = 1
mod = 1000000007
for p in prime_list:
x = p
k = 0
while n//x != 0:
k += (n//x)*(m//x)
x *= p
answer *= pow(p,k,mod)
answer %= mod
print(answer % mod)
여기서 중요한 점이 곱을 하면서 mod로 나눠줘야 곱한 값이 작아지니까 속도가 빨라지는데
answer *= pow(p,k,mod)
answer %= mod
처음에는 pow(p,k,mod)로 p의 거듭제곱을 하면서 mod로 나눠지니까 아무 생각 없이 answer *= pow(p,k,mod)만 했는데 통과를 못하더라
for p in prime_list:
x = p
k = 0
while n//x != 0:
k += (n//x)*(m//x)
x *= p
answer *= pow(p,k,mod)
print(answer % mod)
이게 answer *= pow(p,k,mod)하면서 answer이 기하급수적으로 커지다보니 속도가 최소 10배이상 차이나나봐
answer *= pow(p,k,mod)하고 answer %= mod로 answer을 또 줄여줘야돼
pow(p,k,mod)에만 mod로 압축되는거지 answer은 계속 수가 곱해지니까 계속 커지잖어
이거 한줄이 속도가 10배이상 차이나게 만들더라고...
아무튼 찾아낸게 실력이 늘었단거지
'정수론' 카테고리의 다른 글
| 약수의 합이 짝수인지 홀수인지 바로 알 수 있을까?(시그마 함수의 성질 + 제곱수의 개수 바로 구하기) (0) | 2023.06.26 |
|---|---|
| 팩토리얼을 계산하지 않고도 소인수분해하는 기본기 (0) | 2023.06.24 |
| 자연수를 더해서 최소공배수를 최소로 만들기 (0) | 2023.06.17 |
| harmonic lemma 응용하기 - 올림으로 된 조화수열 합을 빠르게 구하는 방법 (0) | 2023.06.17 |
| 1부터 n까지 모든 자연수들 각각의 약수의 누적합을 구하는 방법들(double counting, harmonic lemma, dynamic programming) (0) | 2023.06.15 |

