1. 문제
2247번: 실질적 약수
첫째 줄에 CSOD(n)을 1,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
1부터 n까지 각각 약수들 중 1과 자기 자신을 제외한 약수들의 합들의 누적합을 구하는 문제
2. 방법1
가장 쉬운 방법은 1부터 n까지 순회해서 각 자연수를 i라고 한 다음, i에 대한 모든 약수를 구해서 1과 자기 자신을 제외하고 더하면 된다
약수는 $O(\sqrt{n})$ 알고리즘으로 모두 나눠보는 방식으로 구한다
그런데 p = 1부터 시작하면, i를 1로 나누면 1과 i를 더하게 되는데 실질적 약수라면 1과 i를 제외한 나머지들의 합을 구해야하니
p = 2부터 시작하는게 핵심
n = int(input())
answer = 0
for i in range(1,n+1):
p = 2
while p*p <= i:
if i % p == 0:
if i/p == p:
answer += p
else:
answer += (p + i//p)
p += 1
print(answer % 1000000)
이렇게하면 시간복잡도는 $O(N\sqrt{N})$이라 2초안에 통과를 못함
2억 * 20만해서 40억만? 아무튼 하루종일 해도 못할듯
3. 방법2(double counting)
조금 더 효율적으로 접근하는 방법은, 1부터 n까지 모든 약수를 한번 나열해보면 패턴을 볼 수 있다
중요한 테크닉중 하나라 기억해두면 좋다
"약수를 세는 것보다 배수를 세는 것이 더 쉽다"
1부터 8까지 각 약수를 한번 나열해보면

세로로 1,2,3,4,5,6,7,8 각각이 몇개인지 세보면
1은 8개 2는 4개 3은 2개 4는 2개 5는 1개 6은 1개 7은 1개 8은 1개

이 개수는 어떻게 구할 수 있을까?
구체적으로 1부터 n까지 모든 약수의 합을 구하는데 1은 몇개 있을까?
당연히 n개 있다.
2는 몇개 있을까? n//2개 있다. 실제로 8을 2로 나눈 몫이 4라서 2가 4개 있다
3은 몇개 있을까? n//3개 있다. 실제로 8을 3으로 나눈 몫이 2라서 3이 2개 있다
...
i는 몇개 있을까? n//i개 있다.
그리고 n//i개는 사실 1부터 n까지 i의 배수의 개수를 나타낸다.
이러한 사실을 이용한다면 $O(N)$에 위 문제를 해결할 수 있다
n = int(input())
answer = 1
for i in range(2,n+1):
k = n//i
if k == 1:
break
answer += i*k
answer -= ((i-1)*i//2)
print(answer % 1000000)
1과 자기자신을 제외한 약수들의 합을 구해야하는데, n//i가 1이 되는 순간 반복문을 탈출하면
내가 더하는 부분은 아래 빨간색 동그라미 부분이다.
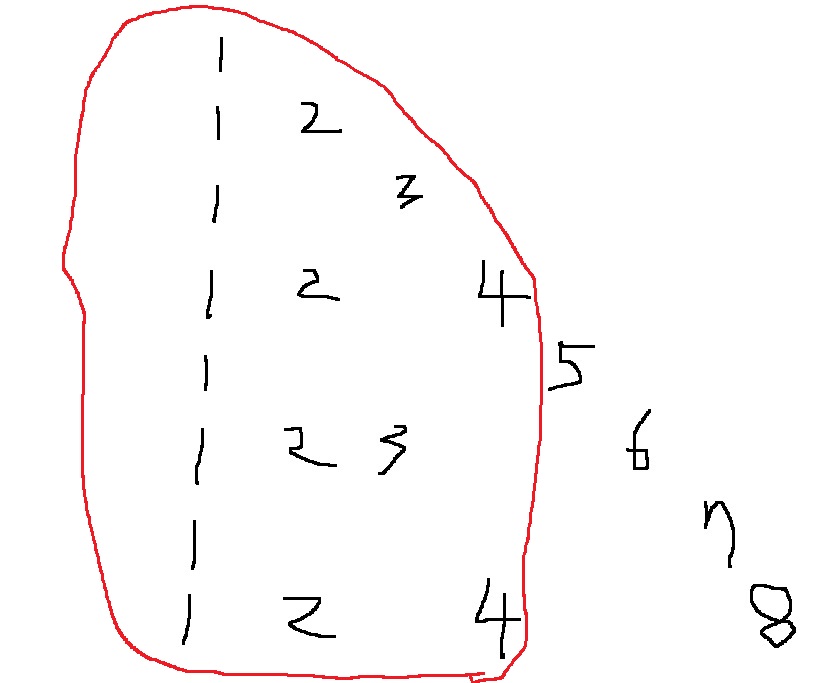
반복문을 탈출하고 나면 내가 제외해야하는 부분은 1 8개랑 1부터 i-1까지의 합이 된다

4. 방법3(harmonic lemma)
위 문제는 결국 다음 식의 값을 구하는 문제로 바뀐다
$$\sum_{i = 1}^{n} i * \left \lfloor \frac{n}{i} \right \rfloor$$
n = 8인 경우, $\left \lfloor \frac{n}{i} \right \rfloor$의 값은 위에서 볼 수 있듯이, i = 1부터 8까지에 대하여 8,4,2,2,1,1,1,1로 나타난다.
n = 10인 경우 10,5,3,2,2,1,1,1,1,1
n = 16인 경우 16,8,5,4,3,2,2,2,1,1,1,1,1,1,1,1
보면 뒤로 갈수록 같은 값을 가지는 정수들이 많이 등장하는 것 같다
------------------------------------------------------------------------------------------------------------------------------------------
다행히도 다음과 같은 정리가 n에 대해 서로 다른 값의 개수를 알려주는데 harmonic lemma라고 부른다
$1 \leq i \leq n$에 대하여, $\left \lfloor \frac{n}{i} \right \rfloor$을 원소로 가지는 집합의 원소의 개수는 $2\left \lfloor \sqrt{n} \right \rfloor$개 이하이다.
증명)
$1 \leq i \leq \left \lfloor \sqrt{n} \right \rfloor$이면, 서로 다른 i가 $\left \lfloor \sqrt{n} \right \rfloor$개라서,
대응하는 서로 다른 $\left \lfloor \frac{n}{i} \right \rfloor$ 역시 많아야 $\left \lfloor \sqrt{n} \right \rfloor$개이다.
$\left \lfloor \sqrt{n} \right \rfloor < i \leq n$일 경우, $1 \leq \left \lfloor \frac{n}{i} \right \rfloor \leq \left \lfloor \frac{n}{\left \lfloor \sqrt{n} \right \rfloor} \right \rfloor = \left \lfloor \sqrt{n} \right \rfloor$이므로,
서로 다른 $\left \lfloor \frac{n}{i} \right \rfloor$의 개수는 많아야 $\left \lfloor \sqrt{n} \right \rfloor$개이다.
(중복이 없으면 최대 $\left \lfloor \sqrt{n} \right \rfloor$개)
그러므로 모든 경우에 대해 서로 다른 $\left \lfloor \frac{n}{i} \right \rfloor$의 개수는 $2\left \lfloor \sqrt{n} \right \rfloor$개 이하이다.
---------------------------------------------------------------------------------------------------------------------------------------------------
이 정리는 $\left \lfloor \frac{n}{i} \right \rfloor$을 같은 값들끼리 묶는다면
최대 $2\left \lfloor \sqrt{n} \right \rfloor$번 계산하면 된다는 것을 의미한다.
그러므로 위 문제를 $O(\sqrt{n})$에 해결할 수 있다.
하지만 특정한 $\left \lfloor \frac{n}{i} \right \rfloor$이 몇개나 있는지 알아야 계산할 수 있다
n = 16인 경우 16,8,5,4,3,2,2,2,1,1,1,1,1,1,1,1이 나오는데, 서로 다른 값 16,8,5,4,3,2,1이 나온다는 것은 알지만
정확히 계산할려면 각 값들이 몇개나 있는지를 알아야 전체 값을 계산할 수 있으니까
$$\left \lfloor \frac{n}{i} \right \rfloor = x$$라고 하자.
$$x \leq \frac{n}{i} < x+1$$이고, $$\frac{1}{x+1} < \frac{i}{n} \leq \frac{1}{x}$$
그러므로, $\frac{n}{x+1} < i \leq \frac{n}{x}$을 만족하는 모든 정수 $i$에 대하여 $\left \lfloor \frac{n}{i} \right \rfloor = x$이다.
그러면 x가 나오게 하는 i는 $\frac{n}{x+1} < i \leq \frac{n}{x}$을 만족하는 i와 같은데 어떻게 구할 수 있을까?
조금 어렵다면 다음과 같이 예를 들어 생각해보자
2.345... < i <= 4.8721...
그러면 i = 3,4로 2개인데 2.345..를 정수로 만든 2보다 큰 3부터 4.8721..을 정수로 만든 4까지이다.
이러한 모든 i에 대해 $\left \lfloor \frac{n}{i} \right \rfloor = x$이다.
가능한 $i_{n}$에 대하여, $i_{1}x + i_{2}x + ... = x * (i_{1} + i_{2} + ...)$으로 구해진다.
즉 i에 대한 부등식의 상한과 하한을 이용해서 합을 빠르게 구할 수 있다.
가능한 i의 합 3+4는, $\sum_{k = 1}^{\left \lfloor \frac{n}{x} \right \rfloor} k - \sum_{k = 1}^{\left \lfloor \frac{n}{x+1} \right \rfloor} k$으로 빠르게 구할 수 있다.
여기서 중요한 점은 다음 i를 어떻게 빨리 찾을 수 있느냐가 시간복잡도를 줄이는데 핵심이다.
2.345... < i <= 4.8721...에서 i = 5로 바로 넘어가줘야한다.
현재 i = 3이고 부등식의 길이 int(4.8721...) - int(2.345...) = 2를 더한 값인 i = 5부터 시작하면 된다
i값을 어떻게 저장하고 있느냐에 따라, 부등식의 길이만 더해서 다음 i로 빠르게 이동할 수 있다.
--------------------------------------------------------------------------------------------------------------------------------------------------
i = 1부터 시작해서 x = n//i로 초기화하고 start = n//(x+1), end = n//x로 부등식의 하한, 상한을 초기화
가능한 i의 합 k = end(end+1)//2 - start(start+1)//2로 구해준다.
answer에 kx를 더해준다.
다음 i의 시작은 i + (end-start)이다.
x를 계산해준다.
x가 0이 되면 반복문을 탈출한다.
x가 0이 아니라면, 부등식의 하한, 상한인 start = n//(x+1), end = n//x를 다시 계산한다.
from sys import stdin
n = int(stdin.readline())
answer = 0
#i = 1부터 시작해서, x와 i의 부등식 하한 상한인 start,end를 구합니다.
i = 1
x = n//i
start = n//(x+1)
end = n//x
while 1:
#현재 x에 대하여 가능한 i의 합을 구합니다.
k = end*(end+1)//2 - start*(start+1)//2
#k*x를 누적합하고
answer += k*x
#다음 i로 이동합니다.
#부등식의 길이인 (end - start)를 더해주면 다음 i로 이동할 수 있습니다.
i += (end-start)
#현재 i에서 x값을 구해줍니다.
x = n//i
#x의 최솟값은 1이므로, x가 0이 나오면 반복문을 탈출합니다.
if x == 0:
break
#현재 x에 대해 i의 부등식 하한,상한을 구해줍니다.
end = n//x
start = n//(x+1)
#실질적 약수를 구하기 위해 1의 개수 n-1개,
#1부터 n까지의 합을 제외해줍니다
answer -= (n-1)
answer -= n*(n+1)//2
print(answer % 1000000)
5. 문제2
17425번: 약수의 합
두 자연수 A와 B가 있을 때, A = BC를 만족하는 자연수 C를 A의 약수라고 한다. 예를 들어, 2의 약수는 1, 2가 있고, 24의 약수는 1, 2, 3, 4, 6, 8, 12, 24가 있다. 자연수 A의 약수의 합은 A의 모든 약수를 더
www.acmicpc.net
6. 풀이
N이하의 모든 자연수에 대하여 각각의 약수의 합을 구하는데, 이번엔 조금 더 어렵게 최대 T = 100000개의 query가 주어지고 N 제한은 1000000이다.
그런데 추가시간도 없이 1초안에 해결해야한다 어떻게 가능할까?
기본적인 접근법은 query를 해결하기 전에 가능한 모든 N에 대하여 N이하의 약수의 합을 미리 구해놓고 배열에 저장해놓는 dynamic programming을 이용
그리고 매 query를 O(1)에 내놓아야한다.
기본적인 원리는 역시 "약수의 개수를 직접 세는 것보다, 배수의 개수를 세는 것이 쉽다"
1부터 n까지 순회해서 각 정수 i에 대하여...
i부터 n까지 i의 배수인 j는 i를 약수로 가진다.
j = i, 2i, 3i, 4i, .... 들은 모두 i를 약수로 가진다는 사실을 이용해서 배열에 i를 더하는 것이다.
n = 8인 경우를 생각해보자. i = 1인 경우, i = 1의 배수인 j = 1,2,3,4,5,6,7,8 각각은 1을 약수로 가지므로 1을 더해준다.

이번엔 i = 2에 대하여 i = 2의 배수인 j = 2,4,6,8은 2를 약수로 가지므로 2를 더해준다

이번엔 i = 3에 대하여 i = 3의 배수인 j = 3,6은 3을 약수로 가지므로 3을 더해준다.

i = 4에 대하여 i = 4의 배수인 j = 4,8은 4를 약수로 가지므로 4를 더해준다

i = 5에 대하여 i = 5의 배수인 j = 5는 5를 약수로 가지므로 5를 더해준다.
i = 6,7,8도 마찬가지로 j = 6,7,8에 각각 6,7,8을 더해주게 된다.
그래서 최종적으로 배열에 저장되는 수는...
1,3,4,7,6,12,8,15가 된다.
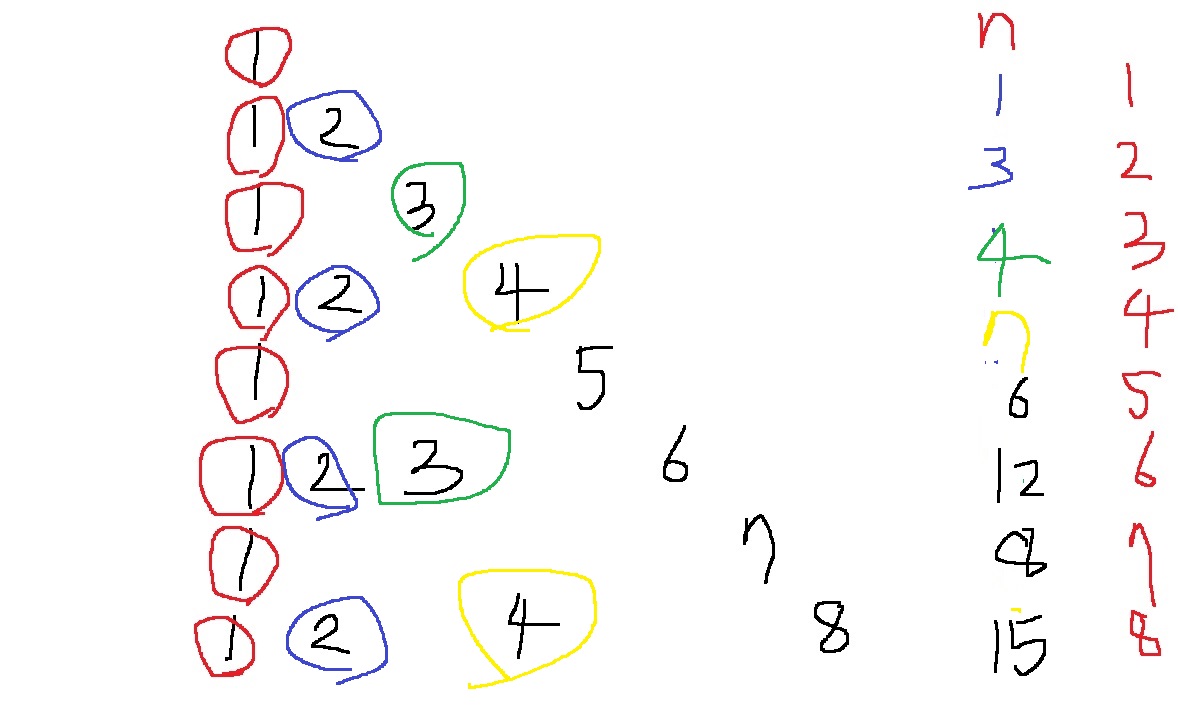
중요한 점은 n에 대해 n 이하의 모든 약수들의 누적합을 구해줘야한다.
n = 8이라 한다면 1+3+4+7+6+12+8+15 = 56이 구해져야한다는 소리
from sys import stdin
T = int(stdin.readline())
n = 1000000
answer = [0]*(n+1)
#1부터 n까지 각 i에 대하여,
for i in range(1,n+1):
#i의 배수인 j는 i를 약수로 가지므로,
for j in range(i,n+1,i):
answer[j] += i #j부분에 약수 i를 더해준다.
#이전 i-1에 구해놓은 약수들의 합을 다음 i에 누적해준다.
answer[i] += answer[i-1]
for _ in range(T):
n = int(stdin.readline())
print(answer[n])
Sum of all divisors from 1 to n - GeeksforGeeks
Sum of all divisors from 1 to n - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
Double Counting과 Harmonic Lemma (tistory.com)
Double Counting과 Harmonic Lemma
※ 이 글을 읽기 전에, 제가 2년도 더 전에 타 블로그에서 썼던 글을 먼저 읽고 오시면 더 좋습니다. ▣ 정수론 시리즈 ─ 순서대로 읽으시는 걸 추천합니다. 1. 뫼비우스 함수와 디리클레 합성곱
xy-plane.tistory.com
Harmonic Lemma (milkclouds.work)
Harmonic Lemma
\[\sum_{i=1}^N \lbrack \frac{N}{i}\rbrack\] 위 식의 결과값은 어떻게 구할 수 있을까? naive하게 구현하면 $O(N)$에 구할 수는 있지만, 훨씬 빠르게 구하는 방법이 있다. $y=\frac{n}{x}$의 함숫값은 $x$가 커질수록
milkclouds.work
Harmonic-Lemma (ahgus89.github.io)
Harmonic-Lemma
약수를 세는 것 보다 배수를 세는 게 쉽다.
ahgus89.github.io
'정수론' 카테고리의 다른 글
| 자연수를 더해서 최소공배수를 최소로 만들기 (0) | 2023.06.17 |
|---|---|
| harmonic lemma 응용하기 - 올림으로 된 조화수열 합을 빠르게 구하는 방법 (0) | 2023.06.17 |
| 최대공약수의 약수는 모든 수들의 공약수이고 최소공배수의 배수는 모든 수들의 배수이다 (0) | 2023.05.28 |
| 베주의 항등식 - 최대공약수로 만들 수 있는 정수 (0) | 2023.05.27 |
| 피보나치 수열 심화과정5 -피보나치 수열의 합을 가장 빠르게 구하는 방법- (0) | 2023.05.27 |

