neural network를 training 하기 전에 input을 normalization해야하는 이유

1. normalization

 

신경망의 훈련을 빠르게 하기 위해 필요한 input normalization

 

다음과 같이 2차원의 입력데이터가 존재할때

 

 

 

주어진 데이터의 평균을 빼고, 표준편차를 나누는 방법으로 normalization할 수 있다.

 

데이터에 평균을 빼서 얻은 새로운 값의 평균은 0이 되고

 

 

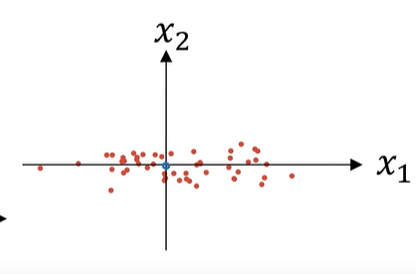
위 그림에서 $x_{1}$이 $x_{2}$보다 분산이 더 큰 특징이 있다.

 

표준편차를 나눠서 얻은 새로운 값의 분산은 1로 되어 $x_{1}$과 $x_{2}$의 산포가 동일해진다.

 

 

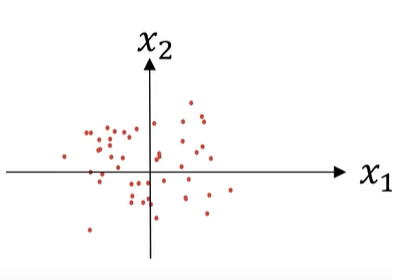
$$Z = \frac{X-\mu}{\sigma}$$

 

$$\mu = \frac{1}{m}\sum_{i = 1}^{m} X_{i}$$

 

$$X = X - \mu$$

 

새로 얻은 X의 평균은 0이므로, 분산은 다음과 같이 구할 수 있다.

 

$$\sigma^{2} = \frac{1}{m}\sum_{i=1}^{m} (X_{i}-\mu)^{2} = \frac{1}{m}\sum_{i=1}^{m} X_{i}^{2}$$

 

2. tip

 

test set을 normalization할때 test set에서 평균과 분산을 추정하지 말고

 

training set에서 사용한 평균과 분산을 사용해서 test set도 normalization하라

 

training set과 test set 각각에서 평균, 분산을 추정한다는 것이

 

두 data set이 서로 다른 분포에서 나왔다고 볼 수 있기 때문에 통계적?으로 안맞다고 볼 수 있어서인가

 

동일한 모집단에서 나왔다고 생각한다면, 동일한 평균, 분산을 사용하는것이 맞긴하지

 

이건 전혀 생각을 못한것 같다.. 허허

 

 

3. 왜 input을 normalizing해야하는가?

 

input을 normalization하지 않으면 각 input의 attribute가 서로 다른 범위의 값들을 가지므로,

 

cost function의 대략적인 모습은 아래와 같이 매우 가늘고 긴 형태의 모습을 띄게 된다.

 

 

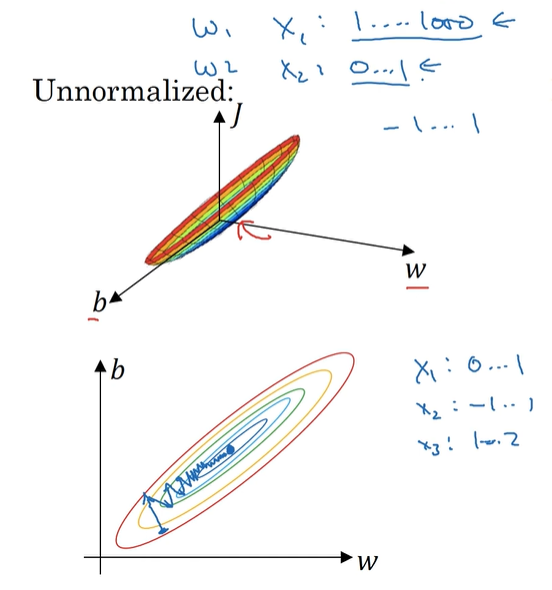
gradient descent에 의해 optimal value를 찾을려면 매우 작은 learning rate를 사용해야하며,

 

그마저도 상당히 왔다갔다 하면서 매우 많은 단계를 거치며 불안정하게 찾아가는 모습

 

데이터를 normalization한다면, attribute의 값 범위가 서로 비슷하므로 다음과 같이

 

cost function이 둥글둥글 구의 형태로 나타난다

 

 

그러면 gradient descent가 적절한 learning rate를 사용하더라도 아주 쉽고 빠르게 optimal value를 찾게 된다

 

실제로는 input의 attribute의 차원이 매우 고차원이기때문에, 위와 같이 2차원으로 보는 것이 100% 적절한 것은 아니지만

 

input을 normalization하여 서로 비슷한 범위의 값을 가지게 한다면, cost function이 둥글둥글한 구의 형태를 지녀

 

optimization하기 쉽다는 대략적인 직관을 얻을 수 있다

 

반드시 학습을 빠르고 정확하게 한다는 보장은 없지만,

 

input feature들간의 크기 범위가 매우 차이가 난다면, 웬만하면 하는 것을 추천한다

 

어떤 값은 0~1 어떤 값은 1~2 어떤 값은 -1~1이면 서로 비슷하니까 굳이 안해도 되긴한데,

 

어떤 값은 0~1 어떤 값은 1~1000 이러면 normalize 하는게 좋다

 

batch normalization이 성능이 좋은 또 하나의 이유가 여기에 있는듯??..

 

If the input variables are combined linearly, as in an MLP [multilayer perceptron], then it is rarely strictly necessary to standardize the inputs, at least in theory. The reason is that any rescaling of an input vector can be effectively undone by changing the corresponding weights and biases, leaving you with the exact same outputs as you had before. However, there are a variety of practical reasons why standardizing the inputs can make training faster and reduce the chances of getting stuck in local optima. Also, weight decay and Bayesian estimation can be done more conveniently with standardized inputs.

 

input이 MLP처럼 선형적으로 결합된다면, 적어도 이론상 input을 표준화할 필요는 거의 없다.

 

그 이유는 weight와 bias를 변화시켜서, input을 rescaling한다면 이전에 했던 것과 완전히 동일한 결과를 낼 수 있기 때문이다.

 

그러나 많은 실용적인 이유로 local optima에 빠질 가능성을 줄이며 학습을 더 빠르게 만들기 위해 input을 표준화할 필요가 있다. 

 

또한 input을 표준화하면 weight decay(regularization)와 bayesian estimation을 편리하게 할 수 있다.

 

 

 

4. 코드 예시

 

간단하게나마 코드로 비교해보면서 진짜로 그런지 알아보자

 

먼저 2차원인 x의 각 차원 값들의 크기가 비슷하다면,

 

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

x_data = [[1, -4], [1, 2], [2, 3], [3, 1],[4, -2], [4, 3], [5, 3], [6, 2], [3, 8], [6, -2]]
y_data = [[0], [0], [0], [0], [0], [1], [1], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)

# 모델 초기화
W = torch.zeros((2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

# optimizer 설정
optimizer = optim.Adam([W, b], lr=0.01)

nb_epochs = 5000
for epoch in range(nb_epochs + 1):

    # [Do it yourself] hypothesis 계산
    hypothesis = 1 / (1 + torch.exp(-(x_train.matmul(W) + b)))

    # [Do it yourself] Cost 계산
    cost = -(y_train * torch.log(hypothesis) + (1-y_train)*torch.log(1-hypothesis)).mean()

    # [Do it yourself] optimizer와 cost를 이용해 모델 파라메터 W,b를 개선

    optimizer.zero_grad()
    cost.backward()
    optimizer.step()
    
    # 100번마다 로그 출력
    if epoch % 1000 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(epoch, nb_epochs, cost.item()))

 

실제로 다음과 같이 learning rate 0.01로도 학습이 잘 되는데

 

Epoch    0/5000 Cost: 0.693147
Epoch 1000/5000 Cost: 0.114669
Epoch 2000/5000 Cost: 0.048685
Epoch 3000/5000 Cost: 0.025061
Epoch 4000/5000 Cost: 0.014071
Epoch 5000/5000 Cost: 0.008265

 

x의 0번째 차원 값을 1000배로 바꾸기만 하더라도

 

x_data = [[1000, -4], [1000, 2], [2000, 3], [3000, 1],[4000, -2], [4000, 3], [5000, 3], [6000, 2], [3000, 8], [6000, -2]]
y_data = [[0], [0], [0], [0], [0], [1], [1], [1], [1], [1]]

 

cost가 바로 발산한다는 것을 알 수 있다

 

Epoch    0/5000 Cost: 0.693147
Epoch 1000/5000 Cost: nan
Epoch 2000/5000 Cost: nan
Epoch 3000/5000 Cost: nan
Epoch 4000/5000 Cost: nan
Epoch 5000/5000 Cost: nan

 

learning rate를 0.001로 낮춘다면,

 

optimizer = optim.Adam([W, b], lr=0.001)

 

cost가 조금씩 잘 떨어진다는 것을 확인할 수 있다

 

물론 learning rate가 작기때문에 처음보다 더 떨어지는 것은 아니지만

 

Epoch    0/5000 Cost: 0.693147
Epoch 1000/5000 Cost: 0.457656
Epoch 2000/5000 Cost: 0.365517
Epoch 3000/5000 Cost: 0.297046
Epoch 4000/5000 Cost: 0.245145
Epoch 5000/5000 Cost: 0.203233

 

learning rate가 작으므로 15000epoch 정도까지 해보면 나름 처음과 비슷한 정도로 cost가 떨어진다

 

Epoch    0/15000 Cost: 0.693147
Epoch 1000/15000 Cost: 0.457656
Epoch 2000/15000 Cost: 0.365517
Epoch 3000/15000 Cost: 0.297046
Epoch 4000/15000 Cost: 0.245145
Epoch 5000/15000 Cost: 0.203233
Epoch 6000/15000 Cost: 0.169309
Epoch 7000/15000 Cost: 0.141433
Epoch 8000/15000 Cost: 0.118328
Epoch 9000/15000 Cost: 0.099115
Epoch 10000/15000 Cost: 0.084945
Epoch 11000/15000 Cost: 0.069767
Epoch 12000/15000 Cost: 0.058599
Epoch 13000/15000 Cost: 0.049269
Epoch 14000/15000 Cost: 0.041463
Epoch 15000/15000 Cost: 0.034913

 

참고

 

 

https://www.youtube.com/watch?v=FDCfw-YqWTE 

Neural Network 적용 전에 Input data를 Normalize 해야 하는 이유 :: GOOD to GREAT (tistory.com)

Neural Network 적용 전에 Input data를 Normalize 해야 하는 이유

 

machine learning - Why do we have to normalize the input for an artificial neural network? - Stack Overflow

Why do we have to normalize the input for an artificial neural network?

 

기본기인데 처음 본것 같냐 왜..

 

진짜 이건 충격적이다