1. non-linear activation
z1 = W1x + b1
a1 = g1(z1)
z2 = W2a1 + b2
a2 = g2(z2)
만약, g1 = px+q, g2 = rx+s의 선형함수라고 한다면, z2 = W2W1(px+q) + W2b1+b2이고,
W2W1 = W3, W2b1+b2 = b3라고 한다면, z2 = W3(px+q)+b3이다.
따라서 몇개의 layer를 연결하더라도, activation이 linear라면, 하나의 layer로 만들어진다.
그래서 함수의 표현력이 떨어져서 hidden layer에서 linear activation은 사용하지 않는다.
output layer에서 linear activation을 사용할 수 있으며, 그렇다면 hidden layer은 non-linear activation으로 ReLU 등을 사용해야한다.
아주 특별한 경우, layer의 압축을 위해 hidden layer에서도 linear activation을 사용하기도 한다.
2. sigmoid derivative
sigmoid g(x)의 도함수는 g(x)(1-g(x))로 나타남
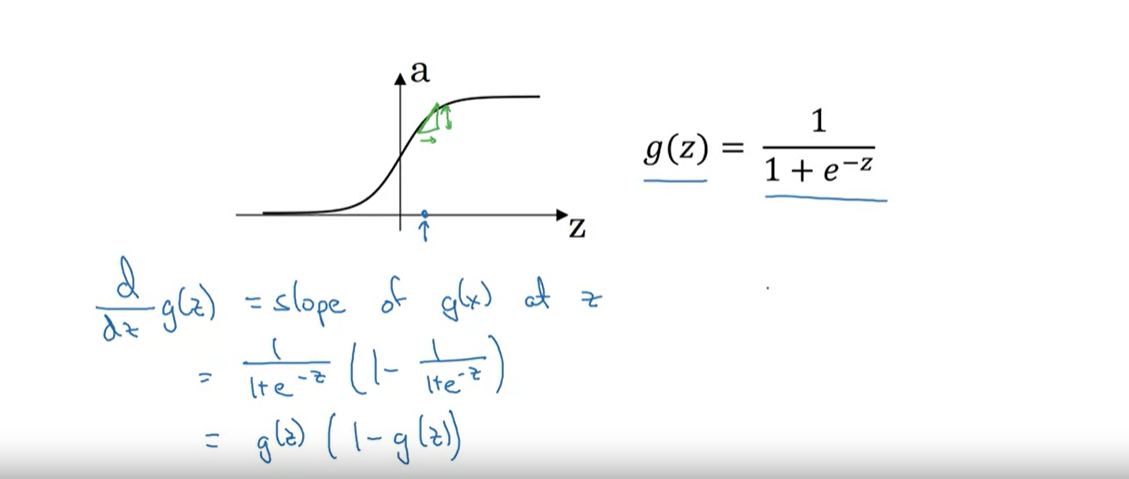
tanh(z)의 도함수는 $(1-(tanh(z))^{2})$

sigmoid와 tanh의 경우 원래 함수 g(z)의 값을 안다면, 미분을 직접하지 않아도, g(z)만으로 도함수를 구현할 수 있다는 것을 보여줌
ReLU와 Leaky ReLU의 경우 도함수는 더 간단하지만, z = 0의 경우 수학적으로 정의되지 않는다.
하지만 컴퓨터로 구현할 때는 z = 0에서 도함수를 1로 정의해도 잘 동작하며, 아주 작은 값으로, 0으로 정의해도 보통 문제되지는 않는다.

3. gradient descent
cost function을 학습하고자 하는 가중치로 미분하여 W = W - (learning rate) * dW로 update

4. random initialization
신경망의 가중치를 모두 0으로 초기화하는 것보다 random하게 작은 수로 초기화하는 것이 학습에 도움이 된다.
가중치 모두 0으로 초기화해버린다면, hidden unit들이 계산하는 값이 초기에 모두 동일하므로 학습이 매우 느려진다.
hidden unit들이 여러개 있는 이유는, 각 unit들이 다른 특징을 냈으면 하는것인데, 모두 같은 값을 계산하면 여러개 있을 이유가 없다.
그래서 초기에 매우 작은 수로 가중치 값들을 초기화하고, 신경망 학습에 들어가는 것이 중요하다.
bias의 경우에는 0으로 초기화해도 크게 문제가 없다고 밝혀졌다.
매우 작은 수로 초기화하는 이유는, activation이 sigmoid나 tanh의 경우 가중치 값을 매우 큰 수로 둔다면,
계산된 값이 매우 커져서 gradient가 매우 작아지므로 초기에 매우 작은 수로 둔다.
물론 다른 activation이면 크게 문제가 없지만, 그래도 작은 수로 두는 것이 좋다.
5. deep neural network
지난 수년동안, shallow model이 할 수 없는 것들을 deep neural network들이 더 잘 기능할 수 있다는 것을 알게되었다.
어떤 주어진 문제에 대해 미리 network가 얼마나 깊어야하는지는 예측하기 어렵지만,
hidden layer의 수를 hyperparameter로 하여 validation set으로 평가해보는 것이 적절하다.

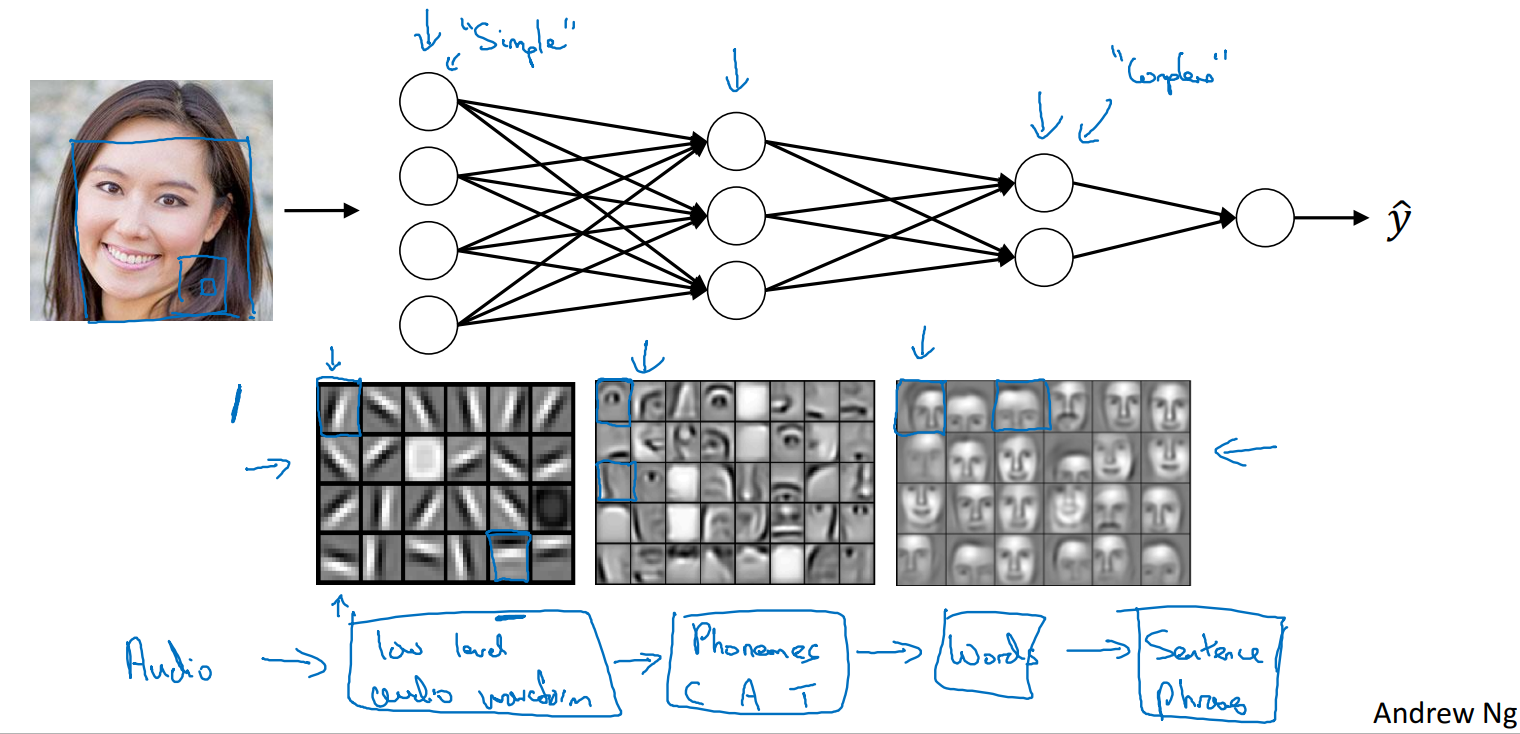
신경망이 깊을수록, low level에서는 데이터의 low level 특징을 찾아내고, high level로 갈수록 이를 이용해서, 더 복잡한 특징을 찾아낸다는 성질이 있다.
얼굴 이미지에서 처음에는 가장자리 edge를 찾아내다가, 갈수록 이를 이용해서 눈, 코, 입, 얼굴형태를 찾아내고 있다.
신경망이 깊을수록 데이터를 더 잘 이해한다는 것
또한, layer의 수가 적으면 한 layer가 너무 많은 hidden unit을 가져야하기 때문에 불리하다.
예시가 이게 맞나..?
XOR을 계산하는데, 신경망 깊이가 깊으면 나눠서 계산할 수 있는데 얕으면 너무 많은 hidden unit이 한층에 배열된다는거

forward, backpropagation의 계산과정 도식화된 그림.. 괜찮아서 가져옴
x로부터 W,b를 이용해 activation값을 계산해나가면서 최종적으로 y를 구하고
y로부터 W,b로 미분하여 backpropagation하는데.. backpropagation으로 구한 dw,db로부터..
w - (learning rate)*dw로 w를 업데이트할 수 있다.
그리고 디테일로 중간 과정에서 나온 WX+b는 저장해두었다가 backpropagation에 사용하면 빠르게 구현 가능

6. hyperparameter
learning rate, #iteration, #hidden layer, #hidden unit, activation function, momentum, mini batch size, regularization,
이런 hyperparameter들이 궁극적으로 parameter인 모델의 가중치 weight, bias를 조절
hyperparameter들의 종류들이 매우 많아짐
나의 문제에 대한 최적의 hyperparameter의 값들은 시도해보면서, 어떤 것이 좋은지 직관을 얻는게 좋다.
learning rate는 0.01도 높다. 0.01보다 더 작게 설정하는게 좋더라... 등등
나의 분야에 대한 hyperparameter들의 최적이 컴퓨터인프라(CPU, GPU 등)가 바뀌면서 몇년 뒤에는 또 바뀔 수도 있다.
7. 인간의 뇌에 비유하는 것에 대하여
forward와 backpropagation이 인간의 뉴런의 학습과정과 비슷하다고 비유하는 경우가 많지만,
뉴런의 학습과정이 명확히 밝혀지지 않았기 때문에 최근들어 인간의 뇌에 딥러닝을 비유하는 일이 많이 줄어들었다
'딥러닝 > Deep Learning Specialization' 카테고리의 다른 글
| 딥러닝 모델 training의 기본 법칙 (0) | 2024.01.12 |
|---|---|
| 딥러닝 시대의 train, validation, test set에 대한 고찰(70:30으로 나눠야하는가? train과 test가 서로 다른 분포? validation vs test는 무슨 차이인가?) (0) | 2024.01.12 |
| 1일차 neural network, supervised learning, activation 간단하게 (0) | 2024.01.10 |
| neural network를 training 하기 전에 input을 normalization해야하는 이유 (0) | 2023.06.07 |
| 딥러닝 모델에서 가중치를 초기화하는 방법(weight initialization) (0) | 2022.03.11 |

