1. 문제
[3, 6, 2, 6, 7, 5, 2] 와 같이 숫자들이 주어졌을 때, 다음 질의에 대해 답하는 프로그램을 작성해보세요.
단, 질의마다 하나의 숫자가 주어지며 해당 번째 숫자를 제외한 다른 숫자들에 대해 인접한 숫자간의 차이의 합을 구해야 합니다.
예를 들어 질의로 5가 주어졌다면 5번째 숫자인 7을 제외한 다른 숫자들을 나열하면 [3, 6, 2, 6, 5, 2]가 되므로
인접한 숫자간의 차이의 합은 |3 - 6| + |6 - 2| + |2 - 6| + |6 - 5| + |5 - 2| = 15가 됩니다.
이때 주어지는 숫자는 1초과 N 미만임을 가정해도 좋습니다.
-------------------------------------------------------------------------------------------------
무작정 코드를 작성한다면, 숫자가 주어질때마다 남은 숫자 N-1개를 순회하여, O(N)시간이 소요되고,
질의가 Q개라면, 시간복잡도는 O(QN)이 된다.
하지만 조금만 생각해보면 놀라운 방법으로 개선시킬 수 있다
예를 들어, 4번째 숫자를 제외했을 경우 답을 구하는 과정은...
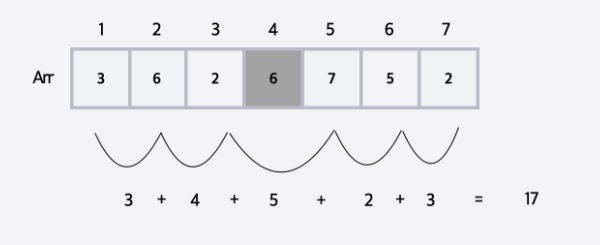
5번째 숫자를 제외하는 경우, 답을 구하는 과정은...

자세히 보면 중복되는 계산이 보이는데.. 적어도 배열에서 [1,3] 구간에서는 계산이 중복되고 있다.
만약 $L_{i}$를 1번부터 i번까지 인접한 숫자간의 쌍의 차이의 합
$R_{i}$를 i번부터 N번까지 인접한 숫자간의 쌍의 차이의 합이라 하고, L,R배열을 구해놓는다면...
그렇다면, i번째 숫자를 제외했을때, 인접한 숫자간의 합을 더 빠르게 구할 수 있을 것이다.
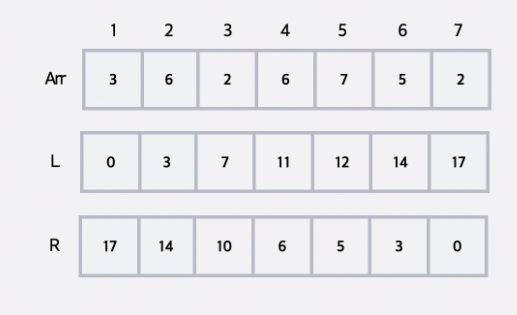
이제 예를 들어 4번째 숫자를 제외한다면...

L배열을 이미 구해놓았다면, [1,3]까지 합이 7로 이미 구해져있다.
그리고 R배열을 이미 구해놓았다면, [5,7]까지 합이 5로 이미 구해져있다.
따라서... $L_{3}$과 $R_{5}$의 합에 3번과 5번사이 차이의 합만 더해준다면... 질의에 답할 수 있다.

일반적으로, i번째 숫자를 제외한다면... $L_{i-1} + R_{i+1} + \left|A_{i+1} - A_{i-1}\right|$로 구할 수 있을 것이다.
미리 L,R배열을 구해놓았다면, 질의마다 O(1)에 문제를 해결할 수 있고, L,R배열은 모두 O(N)에 구할 수 있으므로...
Q개의 질의는 O(N+Q)에 구할 수 있게 된다.
이렇게 왼쪽 방향 L배열과 오른쪽 방향 R배열을 각각 미리 구하여, 중복되는 부분을 효과적으로 줄이는 테크닉을 LR테크닉이라고 부른다.
2. 구현 예시
자바로 구현한 코드는 다음과 같다
public class Main {
public static void main(String[] args){
int[] arr = new int[]{0,3,6,2,6,7,5,2};
int[] L = new int[8];
int[] R = new int[8];
int n = 7;
//L배열을 채워준다.
L[1] = 0;
for(int i = 2; i <= n; i++){
L[i] = L[i-1] + Math.abs(arr[i] - arr[i-1]);
}
//R배열을 미리 채워준다.
R[n] = 0;
for(int i = n-1; i >= 1; i--){
R[i] = R[i+1] + Math.abs(arr[i+1] - arr[i]);
}
//4번째 숫자를 제외할때,
System.out.println(L[3]+R[5] + Math.abs(arr[5]-arr[3]));
}
}
파이썬으로 구현해본다면.. 다음과 같을듯
arr = [0,3,6,2,6,7,5,2]
L = [0]*8
R = [0]*8
n = 7
#L배열을 채워준다.
L[1] = 0
for i in range(2,n+1):
L[i] = L[i-1] + abs(arr[i] - arr[i-1])
#R배열을 채워준다.
R[n] = 0
for i in range(n-1,0,-1):
R[i] = R[i+1] + abs(arr[i+1] - arr[i])
#4번째 숫자를 제외했을 때 답 = 17
print(L[3] + R[5] + abs(arr[5]-arr[3]))
3. 연습문제
n개의 숫자가 주어졌을 때, 서로 인접하지 않도록 3개의 숫자를 적절하게 골라 합이 최대가 되도록 하는 프로그램을 작성해보세요.
4. 풀이
꽤 어려운데??? 왜 쉬운문제지..?
핵심 아이디어는.. 가운데를 이동하면서, 왼쪽에서 최댓값 + 가운데 + 오른쪽에서 최댓값을 모두 구해, 그들 중 최댓값을 구하는 것이다.
구체적으로..
$L_{i}$는 0번부터 i번 원소 중에서 최댓값
$R_{i}$는 i번부터 n-1번 원소 중에서 최댓값
따라서, i = 2,3,4,...,n-3에서 $A_{i}$에 대하여, $L_{i-2} + A_{i} + R_{i+2}$의 최댓값을 구하면 된다.
특히 L배열과 R배열을 O(N)에 구할 수 있어야하는데.. 다음과 같이 구한다면??
L = [0]*n
R = [0]*n
for i in range(n):
L[i] = max(A[:i+1])
for i in range(n):
R[i] = max(A[i:])
인덱싱하면서 O(N)이 되니까.. 각 배열을 $O(N^{2})$에 구하게 된다.
하지만 조금만 더 생각해보면.. L배열의 경우...
0번부터 i번째 원소까지의 최댓값은... i-1번째 원소까지의 최댓값과 i번째 원소중 더 큰 값이 될 것이다.
다이나믹 프로그래밍 방식으로, 이전에 구한 최댓값을 이용해서 구한다면.. O(N)에 구할 수 있다
L = [0]*n
L[0] = A[0]
R = [0]*n
R[n-1] = A[n-1]
for i in range(1,n):
L[i] = max(L[i-1],A[i])
for i in range(n-2,-1,-1):
R[i] = max(R[i+1],A[i])
그래서 파이썬으로 구현하면...
from sys import stdin
n = int(stdin.readline())
A = list(map(int,stdin.readline().split()))
L = [0]*n
L[0] = A[0]
R = [0]*n
R[n-1] = A[n-1]
for i in range(1,n):
L[i] = max(L[i-1],A[i])
for i in range(n-2,-1,-1):
R[i] = max(R[i+1],A[i])
answer = 0
for i in range(2,n-2):
x = L[i-2] + A[i] + R[i+2]
if answer < x:
answer = x
print(answer)
자바에 적용한다면...
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// 여기에 코드를 작성해주세요.
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] arr = new int[n];
for(int i = 0; i < n; i++){
arr[i] = sc.nextInt();
}
int[] L = new int[n];
L[0] = arr[0];
int[] R = new int[n];
R[n-1] = arr[n-1];
for(int i = 1; i < n; i++){
L[i] = Math.max(L[i-1],arr[i]);
}
for(int i = n-2; i >= 0; i--){
R[i] = Math.max(R[i+1],arr[i]);
}
int answer = 0;
for(int i = 2; i < n-2; i++){
int x = L[i-2] + arr[i] + R[i+2];
if(answer < x){
answer = x;
}
}
System.out.println(answer);
}
}
'알고리즘 > 알고리즘 일반' 카테고리의 다른 글
| Python 제곱근 연산 **(1/2)를 함부로 하면 안되는 이유 (0) | 2024.04.12 |
|---|---|
| Python dict indexing보다는 list indexing을 사용해야하는 이유 (0) | 2024.04.12 |
| 자바 알고리즘 기본 -입력을 받는 방법- (0) | 2023.02.15 |
| 파이썬 알고리즘 기본기 EOF(End of File) 배우기 (0) | 2022.12.09 |
| 알고리즘 문제를 풀기위해 2차원 배열에서 이해해야할 테크닉들 (0) | 2022.09.11 |

