1. 2차원 배열 선언
1-1)
일반적으로
[ [0,1,2,3],
[1,2,3,4] ]
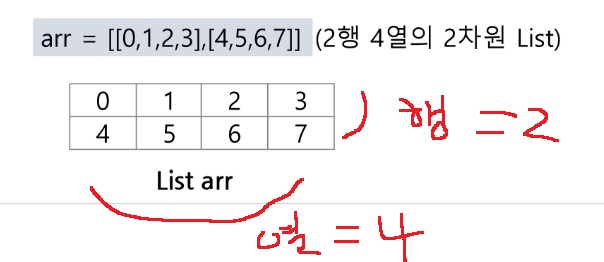
과 같이 [0,1,2,3], [1,2,3,4]는 각각 행을 나타내고 (0,1), (1,2), (2,3), (3,4)는 각각 열을 나타냄
세로의 길이(행의 개수), 가로의 길이(열의 개수)를 필요로 한다
1-2)
입력을 받을때
1 2 3
4 5 6
7 8 9
는 '1 2 3'을 리스트로 바꿀려면, input().split()
123
456
789
는 '123'을 리스트로 바꿀려면 list(input())

2. 2차원 배열 순회하기
2-1) 행 우선 순회
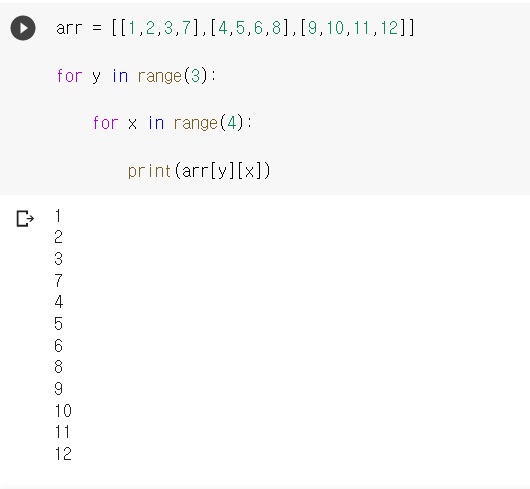
2차원 배열 각 칸의 좌표를 (x,y)라고 하면, arr[y][x]로 접근할 수 있다
n*m 배열에서
for y in range(n):
for x in range(m):
print(arr[y][x])

2-2) 열 우선 순회
여기서부터는 그냥 행 우선 순회에 대한 응용이라고 생각하면 된다
원소에 대한 접근은 무조건 arr[y][x]인데, 열을 나타내는 것은 x이므로, x를 고정시키고 y를 변화시키면 열 원소만 가져올 것
예를 들어 arr[0][0], arr[1][0], arr[2][0]은 0열의 원소
arr[0][1], arr[1][1], arr[2][1]은 1열의 원소
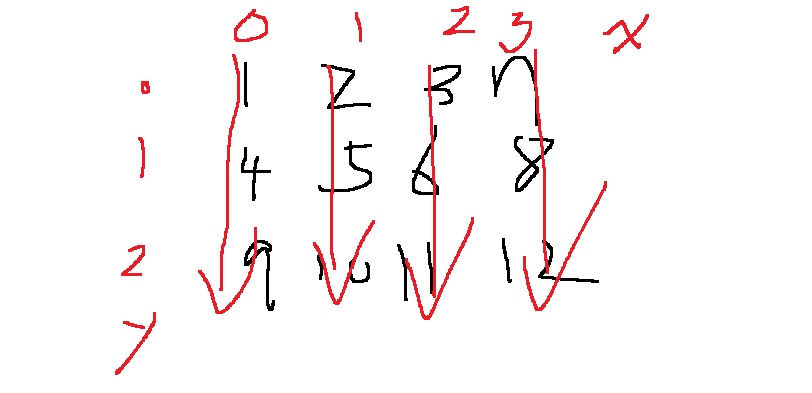

2-3) 지그재그 순회??
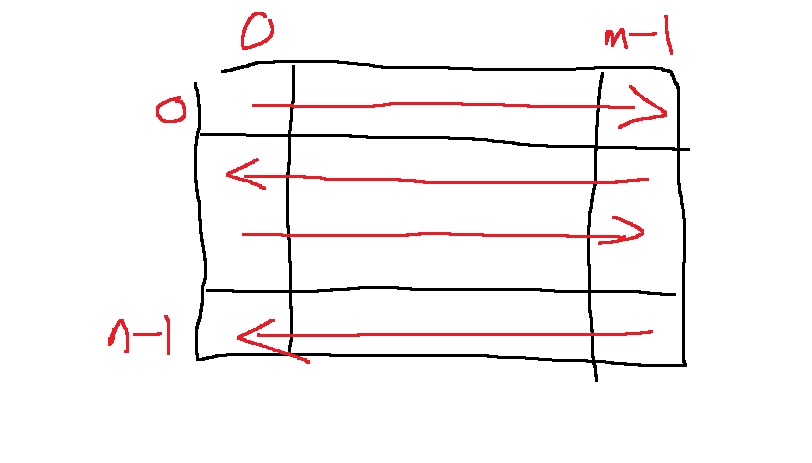
위와 같이 접근할려면 어떻게 해야함??
0행에 대해 0~m-1 순회하고
1행에 대해 m-1 ~ 0 순회하고
2행에 대해 0~m-1 순회하고..
단순하게 하면 이렇게 할 수 있나?
행 y가 짝수이면.. 0~m-1 순회하고 홀수이면 m-1~0 순회하도록

이렇게도 가능하다는데 이건 생각하기 너무 어려운것 같은데

3. 델타배열 접근
2차원 배열의 한 좌표에서 특정한 방향으로 움직이는 방법은..?
예를 들어 (x,y)에서 상하좌우 1칸씩 움직여 접근하는 방법은?
d_x = [0,0,1,-1]
d_y = [1,-1,0,0]
이라는 델타 배열을 만들고
for y in range(n): for x in range(m):
#탐색할 x,y좌표 찾고
#4방향 좌표 nx,ny를 얻으며 for k in range(4): nx = x + d_x[k] ny = y + d_y[k] if nx>=0 and nx<=m-1 and ny >= 0 and ny <= n-1: ##2차원 배열 내에서 유효한 좌표라면.. print(arr[ny][nx])
arr = [[1,2,3,7],[4,5,6,8],[9,10,11,12]]
d_x = [0,0,1,-1]
d_y = [1,-1,0,0]
for y in range(3):
for x in range(4):
for k in range(4):
nx = x + d_x[k]
ny = y + d_y[k]
if nx >= 0 and nx <= 4-1 and ny >= 0 and ny <= 3-1:
print(arr[ny][nx])
4 2 5 3 1 6 7 2 8 3 9 1 5 10 2 6 4 11 3 8 5 12 7 6 4 10 5 11 9 6 12 10 8 11
4. 정방행렬의 특징
단 1번의 순회로 행방향, 열방향을 모두 얻을 수 있다.
행방향 순회
for y in range(n):
for x in range(n):
print(arr[y][x])
에서 x,y 좌표 뒤집어서 넣으면 열방향 순회가 된다
for y in range(n):
for x in range(n):
print(arr[x][y])

5. 전치행렬
전치행렬은 정방행렬에서 x,y 좌표의 값과 y,x 좌표의 값을 서로 뒤바꾼 행렬이다

6. 대각선에 대한 접근
n차원 정방행렬에서 대각선에 대한 원소는 어떻게 찾나?
인덱스를 다 써보면
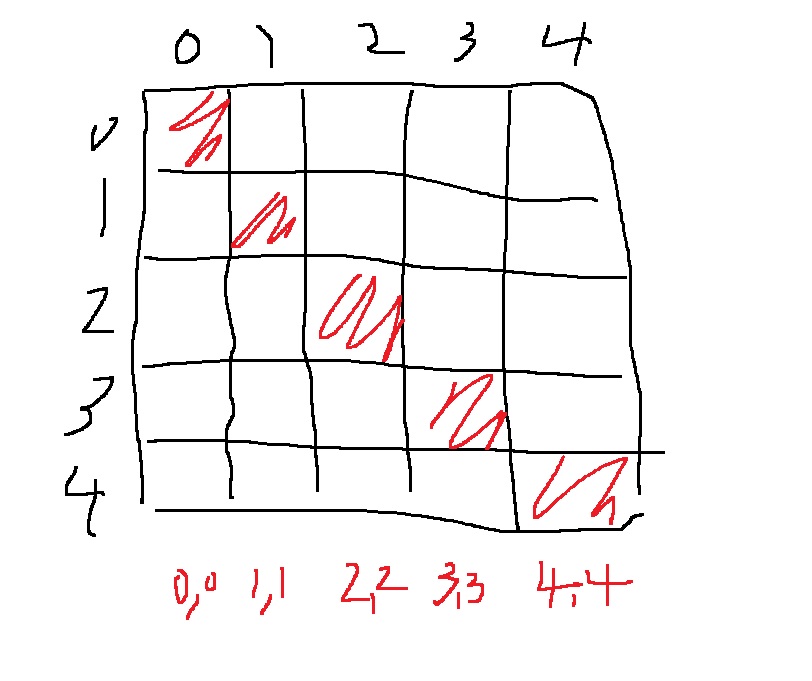
왼쪽에서 오른쪽으로 내려가는 대각선은 x,y 좌표가 서로 같다

근데 위와 같이 물론 가능하지만 모든 원소에 다 접근할 필요가 있을까
for y in range(n):
for x in range(n):
if x == y:
print(arr[y][x])
모든 원소에 다 접근하면서, x와 y가 같은지 조건검사도 하는 비효율적인 검사를 할 필요가 있나
어차피 x와 y가 같은 원소만 고르면 되는데
반대쪽 오른쪽 위에서 왼쪽 아래로 내려가는 대각선은..?

n*n 배열에서 자세히 보면 x,y의 합 x+y가 n-1과 같은 x,y는 오른쪽 위에서 왼쪽 아래로 내려가는 대각선과 같다

근데 역시 x+y == n-1이니까 x만 알아도 y는 n-1-x로 바로 결정되니까 for문 하나만 돌아도 되겠지

7. 원소 합의 최댓값
조건을 만족하는 원소 합의 최댓값은..?
예를 들어 2차원 배열의 각 행의 합에 대해 최댓값은?
변수 초기화에 주의해야한다
max_sum = 0 #max 초기화
for y in range(n): ## 행 y로 고정
row_sum = 0 #행의 합 변수 초기화
for x in range(n): # 행의 합 구하기
row_sum += arr[y][x]
if max_sum < row_sum:
max_sum = row_sum ## 행의 합을 구하면 최댓값 갱신
n = 5
arr = [[1,2,3,4,5],[6,7,8,9,10],[11,12,13,14,15],[16,17,18,19,20],[21,22,23,24,25]]
max_sum = 0
for y in range(n):
row_sum = 0
for x in range(n):
row_sum += arr[y][x]
if max_sum < row_sum:
max_sum = row_sum
print(max_sum)
115
열 순회를 하면 열의 합의 최댓값도 구할 수 있겠지
n = 5
arr = [[1,2,3,4,5],[6,7,8,9,10],[11,12,13,14,15],[16,17,18,19,20],[21,22,23,24,25]]
max_sum = 0
for x in range(n):
row_sum = 0
for y in range(n):
row_sum += arr[y][x]
if max_sum < row_sum:
max_sum = row_sum
print(max_sum)
75
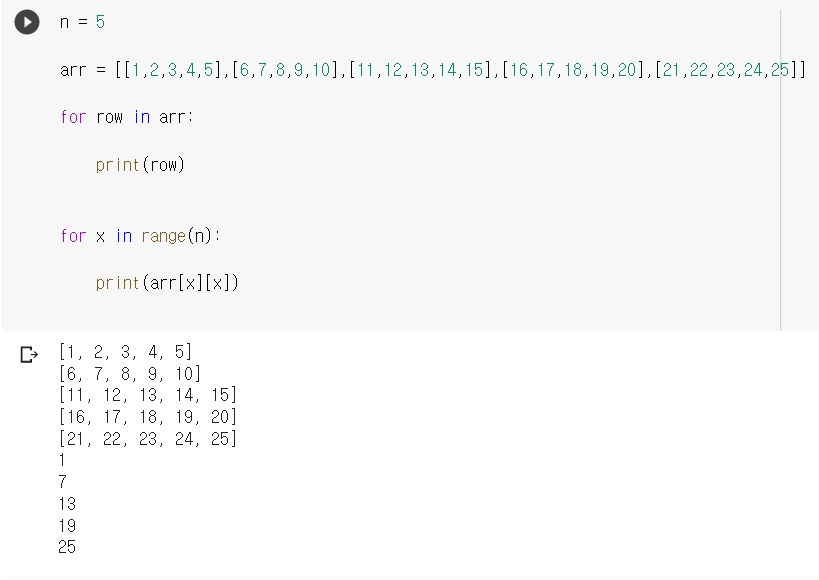
대각선의 합???
대각선 원소를 접근해서 합을 구해보면 되겠지
n = 5
arr = [[1,2,3,4,5],[6,7,8,9,10],[11,12,13,14,15],[16,17,18,19,20],[21,22,23,24,25]]
diag_sum = 0
diag_sum2 = 0
for x in range(n):
diag_sum += arr[x][x]
diag_sum2 += arr[x][n-1-x]
print(diag_sum)
print(diag_sum2)
65
65
양 대각선의 합을 구해보라하면??
근데 양 대각선은 크기가 홀수인 정사각행렬이면 가운데 원소가 중복된다는 점에 주의해야함
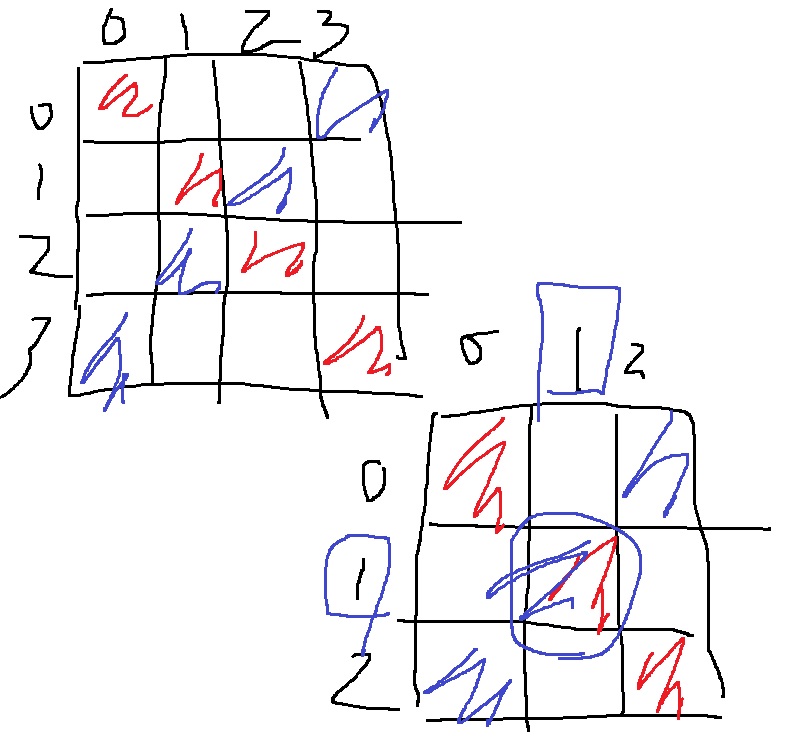
중복되는 가운데 원소의 좌표는 (시작+끝)//2 혹은 0부터 n-1까지 시작이니까, (n-1)//2겠지
n = 5
arr = [[1,2,3,4,5],[6,7,8,9,10],[11,12,13,14,15],[16,17,18,19,20],[21,22,23,24,25]]
diag_sum = 0
for x in range(n):
diag_sum += arr[x][x]+arr[x][n-1-x]
if n % 2 == 1:
mid = (n-1)//2
diag_sum -= arr[mid][mid]
print(diag_sum)
117
대각선 기준으로 양쪽 합들의 크기는 어떻게 비교할까
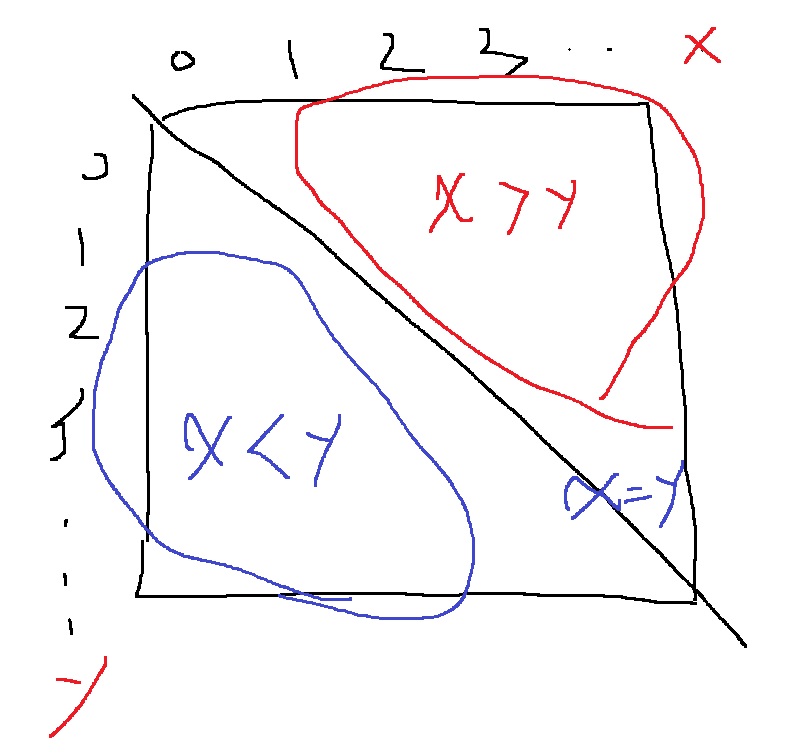
그림그려서 생각해보면 위와 같겠지
x좌표가 y좌표보다 큰 부분은 빨간색 부분이고 작은 부분은 파란색 부분
n = 5
arr = [[1,2,3,4,5],[6,7,8,9,10],[11,12,13,14,15],[16,17,18,19,20],[21,22,23,24,25]]
red_sum = 0
blue_sum = 0
for y in range(n):
for x in range(n):
if x > y:
red_sum += arr[y][x]
elif x < y:
blue_sum += arr[y][x]
print(red_sum,blue_sum)
90 170
한번 순회하면서 x>y인 부분을 red_sum에 더하고 x<y인 부분을 blue_sum에 더하고
근데 정사각행렬이면, x,y를 y,x로 넣어서 열순회도 동시에 할 수 있으니까
그리고 사실 조건문조차도 안 쓸수 있는데
for y in range(n): 이면.. y에 값이 저장되어 있고
x>y인 x를 가져올려면 for x in range(y+1,n):으로 y+1,...,n-1까지 얻을 수 있겠지
이렇게 연속으로 for문을 구성하는 기술도 중요함
n = 5
arr = [[1,2,3,4,5],[6,7,8,9,10],[11,12,13,14,15],[16,17,18,19,20],[21,22,23,24,25]]
red_sum = 0
blue_sum = 0
for y in range(n):
for x in range(y+1,n):
red_sum += arr[y][x]
blue_sum += arr[x][y]
print(red_sum,blue_sum)
90 170
반대 대각선도 생각해볼 수 있겠지?
오른쪽 위에서 왼쪽 아래로 내려가는 대각선은 x+y == n-1인 부분이니까..
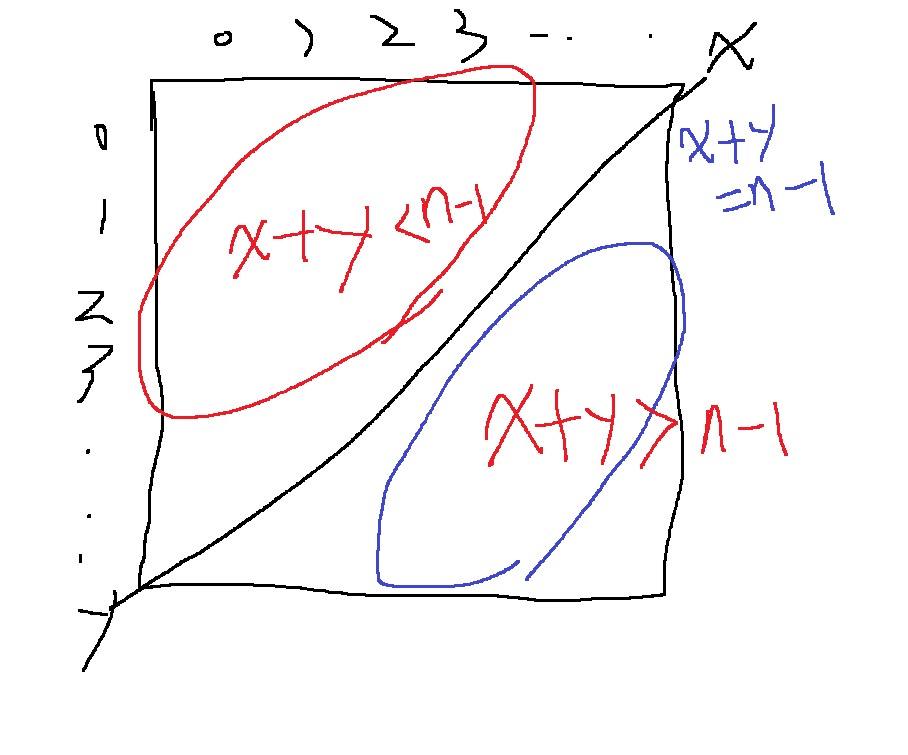
그러면 위랑 똑같은 방식으로 구현하면 되겠지
n = 5
arr = [[1,2,3,4,5],[6,7,8,9,10],[11,12,13,14,15],[16,17,18,19,20],[21,22,23,24,25]]
red_sum = 0
blue_sum = 0
for y in range(n):
for x in range(n):
if x+y > n-1:
blue_sum += arr[y][x]
elif x+y < n-1:
red_sum += arr[y][x]
print(red_sum,blue_sum)
70 190
이 경우에는 대각선이 달라가지고 x,y 바꾼다고 대칭이 되는건 아니니까
조건문 지우는건 조금 어렵겠는데
조금 더 어렵게 해서..

1,2,3,4 크기 비교는 어떻게 할까
위에서 구한 대각선에 대한 조건에서 2가지를 동시에 만족하거나 1가지만 만족하거나... 그런 경우를 구하면 되겠지
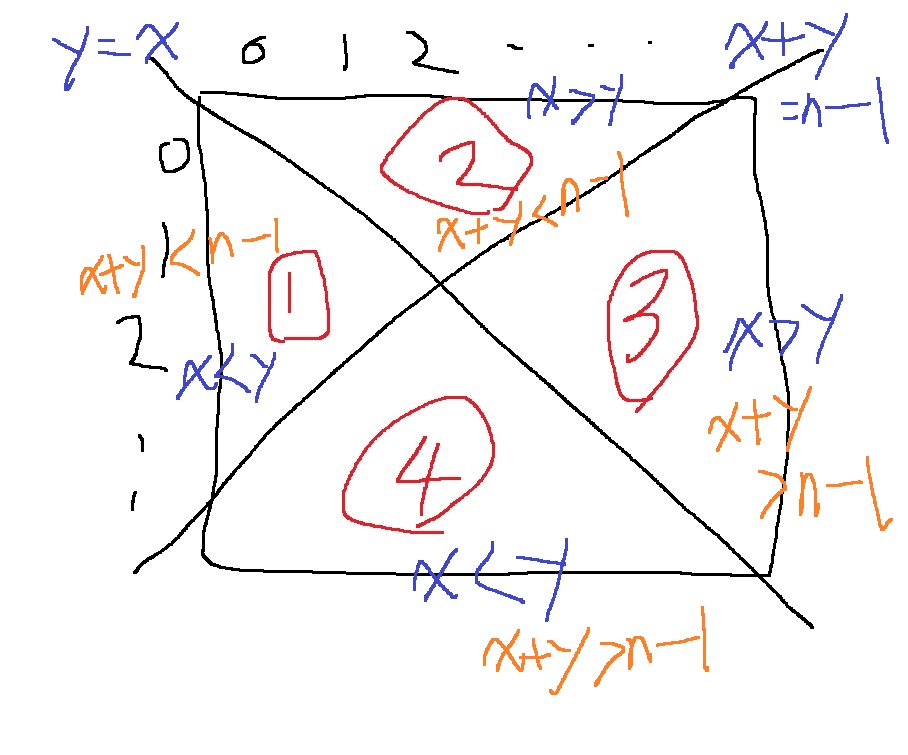
예를 들어서 4번 같은 경우는
y=x 대각선에 대하여 x < y인 경우이면서, x+y = n-1에 대하여 x+y > n-1인 경우를 모두 만족하는 것이겠지
n = 5
arr = [[1,2,3,4,5],[6,7,8,9,10],[11,12,13,14,15],[16,17,18,19,20],[21,22,23,24,25]]
sum1 = 0
sum2 = 0
sum3 = 0
sum4 = 0
for y in range(n):
for x in range(n):
if x > y:
if x+y > n-1:
sum3 += arr[y][x]
elif x+y < n-1:
sum2 += arr[y][x]
elif x < y:
if x+y > n-1:
sum4 += arr[y][x]
elif x+y < n-1:
sum1 += arr[y][x]
print(sum1,sum2,sum3,sum4)
45 17 59 87
8. 심화응용 - 2차원 배열을 1차원으로 나타내는 놀라운 방법
2차원 배열의 각 칸은 (x,y)좌표를 가지는데, 만약 x+y를 각 칸에 적어본다면 무슨 일이 일어날까
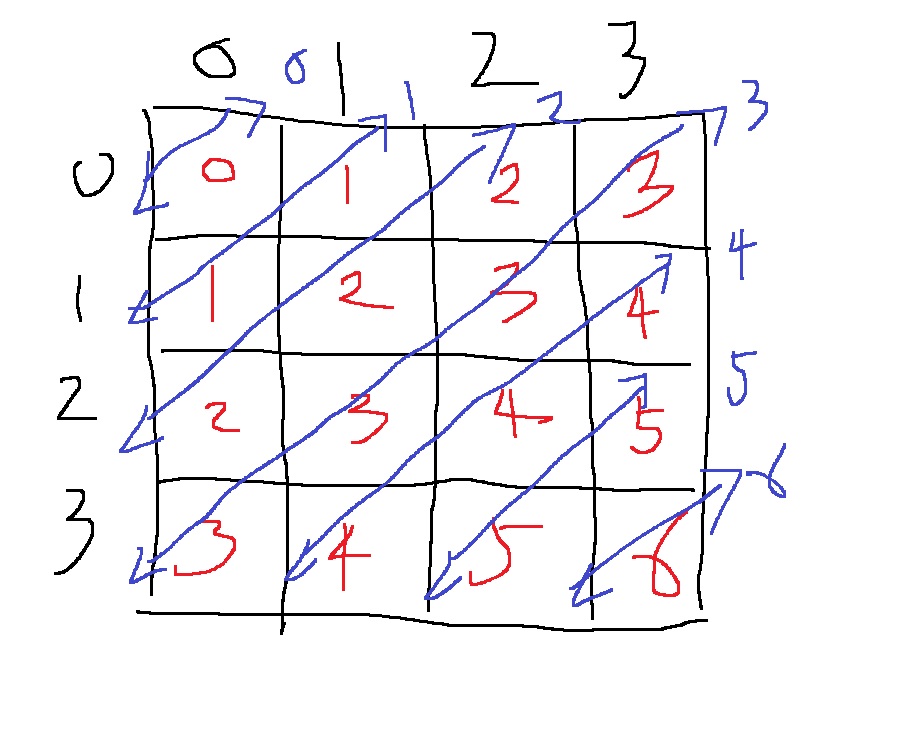
위와 같이 파란색 사선 부분의 값들이 전부 동일하다는 것을 알 수 있다
그러면 위의 2차원 배열은 1차원으로 나타낼 수 있는데
위에서 볼 수 있듯이 4*4배열은 0~3까지 나타난다면, 사선상에 배치할 수 있는 인덱스는 0~6까지이다.
일반적으로 기존에 n*n배열이 0~n-1까지 나타난다면,
사선상에 배치할수 있는 인덱스는 0~2*(n-1)까지 나타난다.
만약에 위 사선에 위치하는 값들의 합중에 최댓값을 구해보라한다면??
각 사선은 0~6까지 인덱스를 가지므로
s = [0]*(2*(n-1)+1)로 초기화할 수 있고
이 배열에 0번에는 0번 사선의 합을 넣고, 1번에는 1번 위치한 값들의 합을 넣고, 2번에는 2번 위치한 값들의 합을 넣고..
n = 5
arr = [[1,2,3,4,5],[6,7,8,9,10],[11,12,13,14,15],[16,17,18,19,20],[21,22,23,24,25]]
s = [0]*(2*(n-1)+1)
for y in range(n):
for x in range(n):
s[x+y] += arr[y][x]
print(s)
print(max(s))
[1, 8, 21, 40, 65, 64, 57, 44, 25]
65
반대 사선은 어떨까? x-y를 각 위치에 적어보면..

역시 반대 사선에 위치한 칸은 x-y의 값들이 전부 동일하다
마찬가지로 한 행의 인덱스가 0~3이라면... -3~3까지 인덱스가 생기므로
일반적으로 0~n-1까지 행의 인덱스는 -(n-1) ~ (n-1)까지 1차원 인덱스로 나타낼 수 있고
비슷하게 s = [0] * (2(n-1)+1))로 초기화 시켜서 각 위치에 배치할 수 있게 된다
특히 -3, -2, -1 같은 음수가 있지만 인덱스는 0 이상이므로 이런 부분에 주의해서
-3은 0, -2는 1, -1은 2, 0은 3에 들어갈 수 있도록.. 생각을 잘 해야함
n = 5
arr = [[1,2,3,4,5],[6,7,8,9,10],[11,12,13,14,15],[16,17,18,19,20],[21,22,23,24,25]]
s = [0]*(2*(n-1)+1)
for y in range(n):
for x in range(n):
s[x-y+(n-1)] += arr[y][x]
print(s)
print(max(s))
[21, 38, 51, 60, 65, 44, 27, 14, 5]
65'알고리즘 > 알고리즘 일반' 카테고리의 다른 글
| 자바 알고리즘 기본 -입력을 받는 방법- (0) | 2023.02.15 |
|---|---|
| 파이썬 알고리즘 기본기 EOF(End of File) 배우기 (0) | 2022.12.09 |
| 중위표기법을 후위표기법으로 바꾸고 이를 계산하는 알고리즘 2편 (0) | 2022.08.22 |
| 사칙연산 중위표기법을 후위표기법으로 바꾸는 알고리즘 1편 (0) | 2022.08.22 |
| 이항계수를 구하는 알고리즘 기초1 - 파스칼의 삼각형 (0) | 2022.08.15 |

