1. 문자열로 된 수식
문자열로 된 계산 수식은 어떻게 계산할까?
eval()함수는 문자열 수식을 받으면 계산해주는데 어떻게 계산하는 것일까?
스택을 이용하면 이러한 문자열 수식을 계산할 수 있다
1-1) 중위표기법의 수식을 후위표기법으로 변경
1-2) 후위표기법 수식을 스택을 이용하여 계산
2. 중위표기법과 후위표기법
중위표기법(infix)은 연산자를 피연산자의 가운데 표기하는 방식
예) A + B
후위표기법(postfix)은 연산자를 피연산자 뒤에 표기하는 방식
예) AB+
컴퓨터가 후위표기법으로 계산을 한다고한다
중위표기법은 계산을 위해서는 앞에서부터 끝까지 읽으면서 왔다갔다해야 수식을 다 계산할 수 있음
왜냐하면 괄호, 사칙연산의 우선순위 때문에
반대로 후위표기법은 한번만 앞에서 끝까지 읽으면 계산을 다 할 수 있음

후위표기법은 위와 같이 연산자를 만나면 그 바로 앞에 2개의 수를 연산시키면 된다
3. 후위표기법으로 변환(사람이 하는 방법)
3-1) 우선순위에 따라 괄호를 사용하여 수식을 재표현함
3-2) 각각 괄호 밖으로 연산자를 뒤로 뺸다
3-3) 괄호를 모두 제거한다

4. 스택을 이용한 후위표기법으로의 변환 알고리즘
4-1) 입력받은 중위표기식 문자열에서 연산자,피연산자 단위문자를 읽는다
4-2) 읽은 단위문자가 피연산자(숫자)이면 출력
4-3) 만약 단위문자가 연산자(괄호 포함)이면 스택의 top에 저장되어 있는 연산자보다 우선순위가 높으면 스택에 push
그렇지 않다면, 스택 top의 연산자보다 단위문자의 우선순위가 높을 때까지, 스택에서 pop을 하고 높아지는 순간 push를 한다
계속 pop을 하다가 스택에 연산자가 없으면 그냥 push한다
4-4) 읽은 단위문자가 오른쪽 괄호(')')이면 스택의 top에 왼쪽 괄호('(')가 나올때까지 스택에 pop을 수행하고 pop한 연산자를 출력함
여기서 왼쪽 괄호 (는 pop만 하고 출력하지는 않는다
4-5) 읽을 것이 없을 때까지 반복함
4-6) 스택에 남아있는 연산자를 모두 pop하여 출력한다
###################################################
연산의 우선순위
딕셔너리로 저장함
스택 밖에서의 우선순위 {'+':1, '-':1, '*':2, '/':2, '(':3}
스택 안에서의 우선순위 {'(':0, '+':1, '-':1, '*':2, '/':2}
여는 괄호가 밖에서는 가장 높았다가 들어오면 가장 낮아짐
#####################################################3
5. 예시를 통한 설명
중위표기법 (6+5*(2-8)/2)를 후위표기법으로 변환

왼쪽부터 차례로 읽어나가는데, 여는 괄호는 밖에서 우선순위가 제일 높으므로 무조건 stack에 push하는데
6은 피연산자이므로 밖에 출력을 함
그 다음 +를 읽는데, 스택에 들어간 (은 연산 우선순위가 0으로 떨어지므로 +가 더 높다. 그래서 stack에 push

다음 5를 읽어서 피연산자이므로 출력을 하고
*은 +보다 우선순위가 높으므로 stack에 push
스택 밖에 있는 (은 우선순위가 제일 높으므로 스택에 push

2를 읽으면 출력하고, -는 스택 안에 있는 여는 괄호 (보다 우선순위가 높으니 push하고
8을 읽으면 출력하고, 근데 문제는 이제 닫는 괄호 )이 들어올때이다.

그러면 다음 여는 괄호가 나올때까지 스택을 pop한다
이때 연산자이면 출력을 하고, 여는 괄호면 그냥 pop만 하고 끝낸다
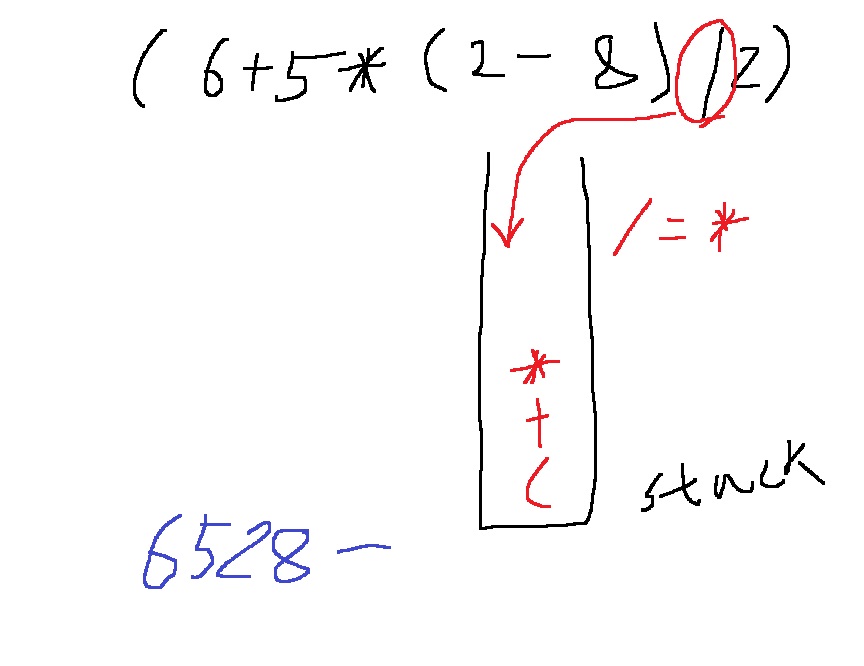
다음에 / 연산자를 읽는데, 스택에 push하는 조건은 /의 연산 우선순위가 스택의 top보다 높을때이다.
그러나 스택의 top에 *이 /와 연산 우선순위가 동일하므로 *을 pop한다.
연산자를 pop하면 출력을 한다.
만약 /의 우선순위가 더 높아지면 그때 /을 push

그러면 *을 pop하고 문자열에 붙인다음, /을 stack에 push하고 숫자 2를 읽으면 다시 문자열에 붙이고
마지막에 닫는 괄호 )을 만나면, stack에 (을 만날때까지 계속 pop을 수행하면서
연산자는 문자열에 붙이므로

6. 예시코드
괄호가 없는 연산, 한자리수로만 이루어진 수식

핵심포인트는 파이썬은 문자로 이루어진 숫자도 부등호로 잘 비교해주면서, 숫자와 연산자 부등식은 무조건 False를 내준다
#괄호가 없는 중위표기식
T = int(input())
operation = {'+':1, '-':1, '*':2, '/':2}
for t in range(1,T+1):
infix = input()
postfix = ''
stack = []
for s in infix:
if s >= '0' and s <= '9': # 만약 s가 피연산자(숫자)이면..
postfix += s #문자열에 그대로 붙여줍니다
else: #만약 s가 연산자이면..
if stack == []: #스택에 아무것도 없으면 그대로 push하고
stack.append(s)
else: #스택에 연산자가 존재한다면..
while stack: #push할때까지 반복하거나, stack에 연산자가 존재하지 않을 때까지 반복합니다.
if operation[stack[-1]] < operation[s]: #스택의 top의 우선순위보다 s의 연산 우선순위가 높으면
stack.append(s)
break #push하는 순간 반복문을 탈출합니다.
else: #스택의 top의 우선순위가 더 높으면..
postfix += stack.pop() #연산자를 pop하여 문자열에 붙여줍니다.
if stack == []: #만약 stack이 빌때까지 push하지 못하고 계속 pop을 수행했다면,
stack.append(s)
#중위표기식에 읽을 것이 없을 때, stack에 남아있는 모든 연산자를 pop하여 붙여줍니다.
while stack:
postfix += stack.pop()
print('#'+str(t),postfix,sep=' ')
1
2+3*4/5
#1 234*5/+
괄호가 존재하면서, 한자리수로만 이루어진 수식?
연산 우선순위를 스택 안에서의 우선순위와, 밖에서의 우선순위 2개를 정의하고
중위표기식을 읽는데 닫는 괄호를 읽는 경우와 그렇지 않은 경우로 나눌 수 있을 것
T = int(input())
#스택 안에서 연산 우선순위와 스택 밖에서의 우선순위를 정의합니다.
instack_operation = {'(':0, '+':1, '-':1, '*':2, '/':2}
outstack_operation = {'+':1,'-':1,'*':2, '/':2,'(':3}
for t in range(1,T+1):
infix = input()
postfix = ''
stack = []
for s in infix:
if s >= '0' and s <= '9': #피연산자이면, 문자열에 그대로 붙여줍니다.
postfix += s
else: #만약에 연산자이면..
if stack == []: #스택이 비어있으면 연산자를 push합니다.
stack.append(s)
else: #스택이 비어있지 않다면 닫는 괄호를 읽는 경우와 그렇지 않은 경우로 나눌 수 있습니다.
if s == ')': #만약 닫는 괄호를 읽는다면
while stack: #스택이 비어있을때 pop을 하는 경우를 방지합니다.
#스택 안에서 여는 괄호를 만날때까지 pop을 하여 문자열에 붙여줍니다.
op = stack.pop()
if op == '(':
break
else:
postfix += op
else: #닫는 괄호를 읽지 않는다면,
#스택안에서의 연산 우선순위를 이용하여 스택의 top의 연산 우선순위와
#스택밖에서의 연산 우선순위를 이용하여 스택으로 들어올려는 s의 연산 우선순위를 비교합니다
while stack:
if instack_operation[stack[-1]] < outstack_operation[s]:
stack.append(s) #만약 s의 연산 우선순위가 더 높으면 push합니다
break #한번이라도 push에 성공하면 바로 반복문을 탈출합니다.
else: #만약 stack의 top의 우선순위가 높으면 pop하여 문자열에 붙여줍니다
postfix += stack.pop()
if stack == []: #stack이 빌때까지 연산자 s를 push하지 못했다면,
stack.append(s) #연산자 s를 그냥 push합니다.
while stack: #중위표기식을 다 읽고도 stack에 연산자가 남아있다면,
postfix += stack.pop() #stack의 연산자를 계속 pop하여 후위표기식에 붙여줍니다.
print('#'+str(t),postfix,sep=' ')
1
(6+5*(2-8)/2)
#1 6528-*2/+
'알고리즘 > 알고리즘 일반' 카테고리의 다른 글
| 알고리즘 문제를 풀기위해 2차원 배열에서 이해해야할 테크닉들 (0) | 2022.09.11 |
|---|---|
| 중위표기법을 후위표기법으로 바꾸고 이를 계산하는 알고리즘 2편 (0) | 2022.08.22 |
| 이항계수를 구하는 알고리즘 기초1 - 파스칼의 삼각형 (0) | 2022.08.15 |
| 약수를 빠르게 구하는 알고리즘 (0) | 2022.08.10 |
| 문제의 핵심을 이해하고 정확히 구현하는 알고리즘 (0) | 2022.08.09 |

