1. 기계학습 구성 요소
경험사례, 모델, 평가기준
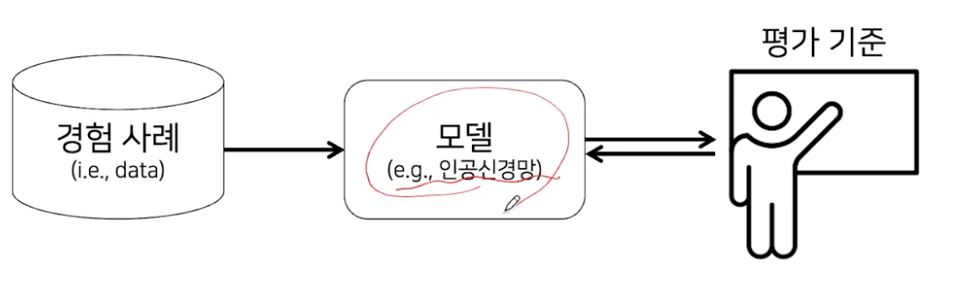
인공신경망 같은 모델을 학습시키고자 한다면..? 많은 경험사례를 통한 반복학습
입력과 기대하는 출력의 pair를 반복적으로 보여줌
모델한테 보여주는건 좋은데 모델이 학습을 잘 하고있는지 기준이 필요함
학습을 못하고있으면 잘하도록 만들어야하니까
이러한 평가 기준이 cost(loss function)
2. 가장 좋은 모델 f를 찾는 방법?
기대하는 출력과 모델이 데이터를 보고 낸 출력 사이 차이가 최소화가 되도록 하는 모델을 찾는 것

기대하는 출력과 모델이 낸 출력 사이 차이를 최소화시키도록 만드는 방향으로 학습
3. 예시로 이해하는 기계학습
시간의 흐름과 주가와의 관계를 파악

시간을 넣어주면 모델이 해당하는 기댓값 주가를 출력
과거의 결과가 다음같이 나온다면...

이러한 데이터들을 설명해주는 모델을 어떤 것으로 선정해야하는가



이차방정식, 선형모델 등을 모두 포괄하는 다양한 형태의 모델이 neural network
neural network를 어떻게 만드느냐에 따라 다양한 관계성을 모델링할 수 있다
neural network를 매우 단순하게 만들어 하나의 linear single layer로 만든다면...
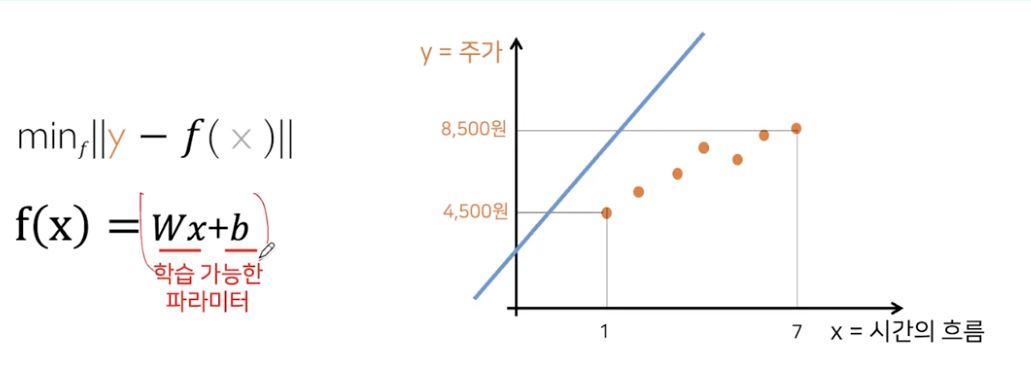
W와 b가 학습 가능한 파라미터로 기대하는 출력 y와 모델이 낸 출력 f(x)의 차이를 최소화시키는 w,b를 찾는게 목적
처음에 w,b를 아무렇게나 주면 위와 같이 엉뚱한 모델이 나옴
기대하는 출력은 노란색 점이고
모델이 낸 출력은 파란 선인데 둘 사이의 차이를 최소화할려면, 당연히 둘 사이의 차이를 측정할 수 있어야함
이를 cost, loss function이라고 부른다

모델의 예측인 f(x)와 목표 y의 차이인 error의 제곱의 합을 평균낸 값으로 정의
예측값 f(x)가 목표 y를 따라갔으면 좋겠음
그러면 cost는 0에 가까울수록 좋은거겠지

위와 같은 모델은 두 점이 3000,8000으로 거리 내에 있다 하더라도 다른 점이 매우 많이 떨어져있다보니.. 적절한 모델이 아니다
W,b에 따라 산의 위치를 나타낸다고 말할 수 있다

직접 그 위치로 가서 해당하는 코스트를 계산하는 평가를 해봐야, 어느정도인지 알 수 있다
처음 위치가 W0일때, 내가 어디로 내려가야하는지는 일단은 모른다
그런데 현재 위치에서 대략 주변을 더듬어보다가 경사가 어느정도인지 추정을 해본다면...
어느곳으로 가면 올라가는 곳이고, 어느곳으로 가면 내려가는 곳인지 알 수가 있어서..
대충 내려가는 방향으로 내려가는거지

다시한번 현재 위치에서 경사를 추정해보고 어디로 가면 내려가는 곳이고
어디로 가면 올라가는 곳인지.. 판단을 해본다. 당연히 내려가는 곳으로 내려가야겠지
이를 반복적으로 생각하면서 하산을 하다보면 최종적으로 내려오는거고
이를 global minima라고 부른다

근데 내려가는 방향이 한곳만 있을까?
매 내려가는 순간순간에 기분?에 따라 다른 방향으로 내려갈 수도 있는거지

그러다보니까 어느 방향으로든 경사를 보니 올라가는 방향이라 현재 지점이 가장 많이 내려왔다고 착각을 하게 됨
이러한 지점을 local minima라고 부른다
4. gradient descent
산을 내려오면서 경사를 더듬어보다가 내려가는 방향을 찾는 과정이 바로 gradient descent이다
업데이트하고 싶은 W라는 parameter로 cost를 미분

미분해서 얻는 값을 gradient라고 부른다
단순히 gradient $\Delta W$방향으로 가면 올라가는 방향이다(증가하는 방향)
그래서 내려가는 방향을 가리키도록 -를 붙여서 업데이트를 함
가는 정도는 $\alpha$만큼 가도록
cost의 W에 대한 미분값을 gradient라고 부르고 - 방향으로 감소시킨다고 해서 gradient descent라고 부른다
궁극적으로는 cost가 최소가 되는 W를 찾고 싶은것
gradient가 감소하는 방향으로 가다보면 그러한 W를 찾을 수 있다는거지

여기서 Learning rate는 user가 결정하는 parameter
여러 training으로 좋은 parameter를 감으로 찾거나
학습에 성공한 여러 논문에서 제시한 값으로 해보거나..
근데 적절한 값으로 설정하는게 중요하다.
매우 큰값으로 세팅한다면... 다음 그림과 같이 아예 내려가질 못함

그렇다고 너무 작게 잡으면.. 매우 느리게 최솟값을 찾아 내려간다
언젠가는 찾겠지만 너무 느리겠지

데이터가 너무 많으면 gradient를 계산하는것 조차도 매우 오래걸릴 수 있음
그런데도 learning rate를 너무 작게 잡으면 훨씬 더 오래걸리겠지
그래서 적절한 learning rate를 잡는것은 중요하다

모델에 데이터를 입력해서 평가를 하고, gradient descent를 통해 parameter 최적화를 하고 다시 평가를 하고
다시 최적화를 반복해서 최적의 모델을 찾는 과정
5. epoch
gradient 계산에는 기본적으로 모든 데이터를 사용해 계산하는 것이 기본인데, 너무 많다보면 너무 오래걸리다보니
데이터를 일부 쪼개서 쪼갠 단위별로 gradient를 계산해 parameter를 업데이트하는 과정이 mini batch gradient descent라고도 부른다
그리고 일부 쪼갠 단위를 mini batch라고 부른다
데이터가 100개라면, 10개의 minibatch로 쪼갠다고 할때, 각 minibatch마다 gradient를 계산해서.. parameter 업데이트를 한다
그러면 100개를 모두 업데이트해볼려면 10 minibatch를 업데이트해야하는데, 이 과정을 모두 하면 1epoch 수행했다고 한다
1epoch은 train dataset을 전부 이용하면 1epoch training했다고 한다
6. 정말로 완벽한 모델인가?
위와 같이 gradient descent로 어떻게 모델을 잘 찾았다고 해보자..

주어진 주황색 점, 학습 데이터에 대해서는 모델이 잘 설명해주지만 실전에서 사용할때는..
주황색 점 부분이 아닌 다른 부분에서 나오는 예상하지 못할 테스트 데이터에 대해서도 모델이 잘 설명해주길 바란다

위와 같이 전혀 본적이 없는 파란색 부분에 대해서는 모델의 에러가 상당히 크게 나올 수 있다.
이런 일이 발생하는 이유는 세상의 모든 데이터를 학습시키지 못했기 때문이다
이를 일반화를 하지 못했다고 부른다
7. 기계학습이란 무엇인가
계산과 추론은 일반적인 법칙 f가 존재해서 f는 정말로 확실하다고 생각하니 input을 주면 output도 당연히 올바르게 나올 것이라고 생각한다
최적화는 input을 주고 대응하는 output이 올바르게 나오는 함수 f를 찾는 작업이다.
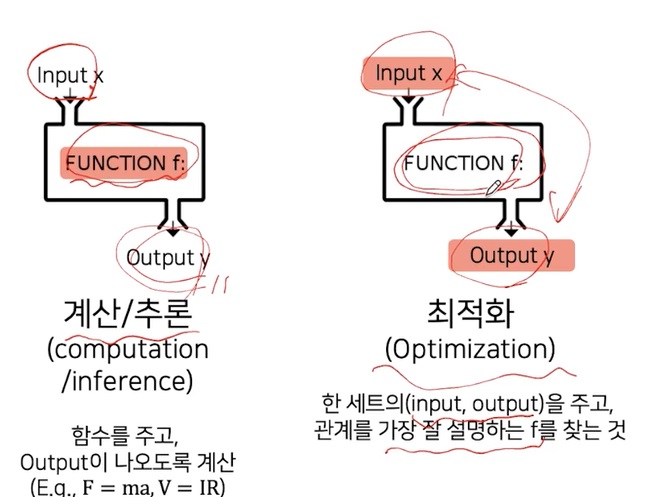
최적화를 어떻게 굉장히 잘 해서 그러한 f를 잘 찾았다고 하더라도 전혀 본적이 없는 input, output에 대해서는 함수 f가 올바르게 output을 낼지는 아무도 모른다
주어진 input에 대해 output을 올바르게 내는게 최고이며 그러한 함수를 찾는게 최적화이다.
하지만 실제로 사용하기 위해서는
우리가 가진 데이터를 학습시켜서 전혀 보지 못했던 input에 대해 어느정도 올바르게 output을 내줘야 한다.
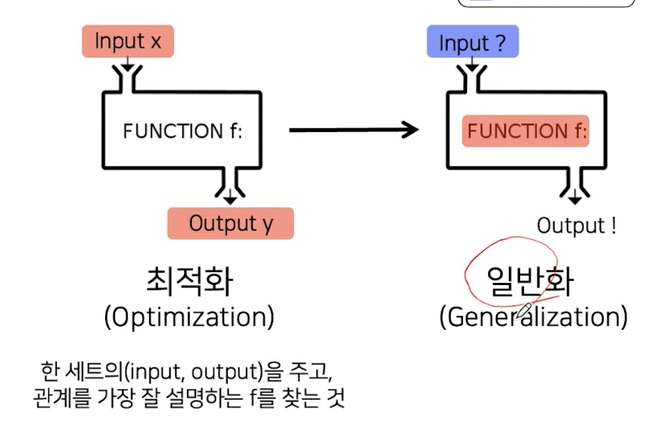
기계학습과 최적화는 일반화에 차이가 있다
기계학습은 최적화를 통해 일반화를 시키는 것을 목적으로 한다
모델이 정말로 주어진 데이터를 잘 학습했다면 그 데이터로부터 파악한 핵심을 전혀 보지 못했던 데이터에 잘 적용해서 올바른 답을 내는것이 지능이다
상당히 어려운 문제
이론적으로 어떤 기준이 있긴하지만 결국 경험적으로 테스트를 해봐야 서비스에 사용할 수 있을지 없을지 판단할 수 있는 법
절대적으로 좋은 모델, 데이터는 존재하지 않으며 해당 서비스에 적절한 모델, 해당 모델에 적절한 데이터.. 등등 모두 경험적으로 많은 실험을 통해 테스트해봐야함
8. 일반화를 잘 할 수 있는 방법들
어떻게 하면 일반화를 조금이라도 더 잘 할수 있을까
1) 충분히 많고 다양한 데이터 사용
이론상 이 세상의 모든 데이터를 전부 알고 있다고 한다면 모든 기계학습 문제를 완벽하게 해결할 수 있다
추론하고자 하는 새로운 데이터가 들어올때 내가 가진 데이터에서 정답을 찾아보면 그만이거든
근데 당연히 이 세상의 모든 데이터를 얻을 수 없으며
가질 수 있다 하더라도 컴퓨터에 저장할 수가 없다
그래서 우리가 가진 데이터를 기계학습 모델에 말 그대로 집어넣는거임
많은 양의 데이터를 보면 볼수록 기계학습 모델이 내가 본 데이터 같은데? 하면서 답을 쉽게 낼 수 있다
2) 모델의 복잡도 줄이기
데이터가 한정되어 있을때, 너무 복잡한 모델을 사용한다면 전혀 예상하지 못한 결과가 나올 수 있다

빨간색 두 데이터를 반드시 지나는 검정색 모델과 파란색 모델이 존재할 때
가운데에 (주황색 부분) 어떤 데이터가 들어올지는 아무도 모른다
너무 복잡하게 하다보면 융통성이 없다보니 갑자기 들어온 주황색 데이터에 대해 에러가 크게 나타나는 경향이 있고
간단하게 파란색으로 나타내면 에러가 적게 나타나는 경향이 있다
근데 당연하지만 항상 그런건 아님
우연히 검정색 모델이 상당히 잘 맞을수도 있다
그래서 실험을 해봐야함
3) 가중치의 regularization
모델의 복잡도를 줄이는 방법의 일종
cost function에서 cost를 줄여나가며 가중치를 업데이트하는데, cost function에 가중치에 관련된 항을 추가하는 것
그러면서 cost를 줄여나가면서 정답을 잘 맞춰나가고자 하는데,
cost에 가중치의 크기도 고려되고 있기 때문에.. 가중치 크기도 어느정도 내가 원하는 범위에 들어와줬으면 한다는 것
4) drop out
모델에 noise를 주는 것
예를 들어보면
input X가 layer로 들어가면서 WX로 output이 나오고 다음 layer로 들어가는데..
들어가기 전에 일부 값을 랜덤하게 0으로 만들어버린다든지.. 데이터에 noise를 강제로 추가함
하지만 그럼에도 불구하고 task loss는 minimize되도록
단순히 input과 output 사이 관계만 학습하는게 아니라 데이터에 noise를 추가해서 전혀 보지 못한 데이터에도 대응할 수 있도록 강인하게 학습시키는 행위
데이터에만 noise를 주는게 아니라 가중치 W를 변형시킬수도 있고.. 여러가지 방법이 많다
9. universal approximation theorem
deep neural network가 충분히 크다면 어떠한 input,output의 관계라도 전부 표현할 수 있다
기존에는 선형모델, SVM, decision tree, ... 등등 정형화된 모델을 사용하여 학습하였지만
이제는 이런 모델들을 deep neural network로 치환하고 그냥 학습을 해버리는 이유가 여기에 있다
어떤 모델을 골라야할지 고민할 필요가 없음
그냥 deep neural network를 사용하면 그만이거든
근데 이제 이미지, 텍스트, 음성 등 각각의 데이터에 성능이 특히 좋다는 모델 아키텍처들이 연구되고 있지
한정된 파라미터로 해당 데이터를 잘 표현하는 아키텍처를 찾는 연구 방향으로 나아가고 있는 것
아무튼 2012 AlexNet 이후로 사람들이 전부 neural network를 사용하기 시작
10. 기계학습 패러다임의 변화
기존에는 데이터를 많이 모아두고 사람이 데이터를 하나하나 보면서, 어떤 특징이 좋을지 따로따로 추출했다
좋은 특징 = 입력과 출력과의 관계를 잘 설명하는 요인
이런 특징을 상당히 잘 만들었다고 한다면.. 분류는 간단한 모델을 사용함
특징 추출이 충분히 강력하다면 분류기가 간단하더라도 상당히 성능이 좋았다
근데 2012 AlexNet이 보여준 것은.. 사람들이 수십년동안 feature engineering으로 특징을 잘 만들었는데..
그럼에도 불구하고 세상은 그렇게 단순하지 않았다는 것
사람들이 생각한 것보다 더 많은 부분을 고려해야했으며 사람이 놓친게 너무 많았다
neural network는 특징 추출을 할 필요없이 그냥 input에서 output을 한번에 이어버림
이것을 end-to-end 구조라고 부름

입력과 출력을 미분 가능한 neural network로 놔두고 통째로 학습
최종단은 분류를 잘하도록 학습이 되고
앞부분은 분류를 잘하기 위해 어떠한 특징을 추출하면 좋을지 알아서 학습하게 됨
이러한 패러다임 변화에는 universal approximation theorem이 맞을 것이라는 믿음에 있다
'딥러닝 > 딥러닝 기초' 카테고리의 다른 글
| pretrained model & transfer learning에 대해 제대로 이해하기 (0) | 2023.05.04 |
|---|---|
| data preprocessing 기본 개념 제대로 이해하기 (0) | 2023.04.28 |
| 인공지능 개론1 2023년 최신판 (0) | 2023.02.24 |
| convolution layer의 parameter 세는 방법 대충 (0) | 2023.01.03 |
| convolution의 backpropagation 대충 (0) | 2023.01.02 |

