1. convolution은 미분해도 여전히 convolution

convolution을 미분하면 도함수와 convolution이 된다.
앞에 있는 f가 커널이라는 거 알지?
2. convolution의 직관적인 계산 그림

처음에는 w1,w2,w3가 x1,x2,x3에 만나서 o1
다음으로 한칸 옆으로 가서 x2,x3,x4를 만나서 o2
다음으로 한칸 옆으로 가서 x3,x4,x5를 만나서 o3
backpropagation을 위해 미분을 해보면 여전히 kernel과의 convolution이 된다는 것을 위에서 보였으므로
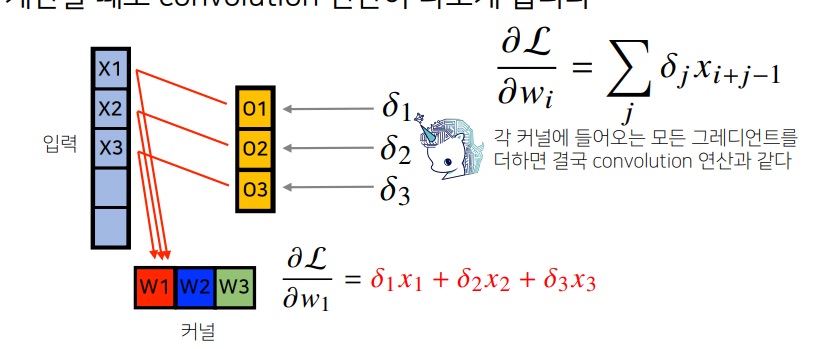
왜 x로 전달되느냐 oi의 미분이 xi이기 때문임
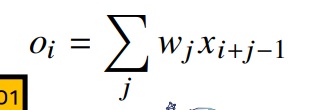
$\delta$는 loss를 o로 편미분한 값이다.

loss를 w로 미분한것이 $\delta$와 x의 곱으로 나타남

convolution을 미분해도 여전히 kernel과의 convolution으로 나타나므로 위와 같이 전달된다.
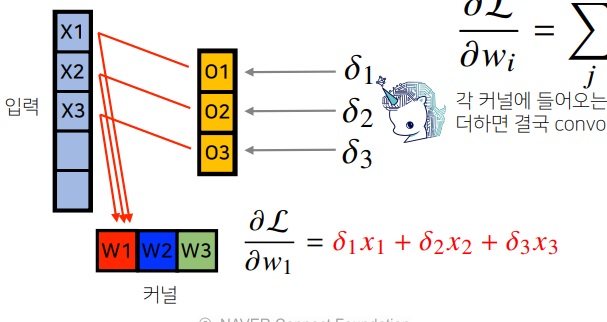
그래서 결과적으로 위와같이 입력과 출력 미분값의 곱의 합으로 구해지는데

근데 이게 maxpooling도 있어야하는데 여기는 그걸 쓰지 않았기도 하고
수식으로 정확히 따라가야할 이유도 모르겠다 다 구현이 돼있잖아
중요한 수식이 너무 어렵다
핵심은... convolution을 미분하면 여전히 해당 kernel과의 convolution으로 나타나서.. 출력이 입력으로 전달되면서...
입출력의 곱의 합으로 나타난다.. 뭐 그런 느낌
다시보니까 backpropagation이 느낌이 영 안오네.. 허허
참조
CNN 역전파 (Backpropagation for CNN) (tistory.com)
CNN 역전파 (Backpropagation for CNN)
이번 포스팅에서는 CNN의 가중치를 학습하기 위한 역전파가 계산이 어떻게 이루어지는지 살펴 보겠습니다. 이번 포스팅에서 이미지 픽셀 좌표는 좌상단에서 0 부터 시작하기로 약속하겠습니다.
yjjo.tistory.com
CNN 역전파를 이해하는 가장 쉬운 방법 (metamath1.github.io)
CNN 역전파를 이해하는 가장 쉬운 방법
본 문서의 목적은 CNN(Convolution Neural Network)의 역전파Back propagation 알고리즘을 정리하기 위해 간단한 CNN 모델을 정의하고 정의된 모델에 해당하는 수식을 완전히 유도하는 것 입니다.
metamath1.github.io
'딥러닝 > 딥러닝 기초' 카테고리의 다른 글
| 인공지능 개론1 2023년 최신판 (0) | 2023.02.24 |
|---|---|
| convolution layer의 parameter 세는 방법 대충 (0) | 2023.01.03 |
| batch size는 어떻게 설정해야하는가? (0) | 2022.12.31 |
| 머신러닝 모델링 기본방법 - bootstrapping, bagging, boosting (0) | 2022.12.31 |
| 확률분포&연속형분포의 이산화&조건부분포&기댓값으로 구하는 통계량 (0) | 2022.06.02 |

