1. 특정한 구간에 존재하는 모든 수의 합
어떤 수열이 주어질때, 만약 특정 구간 [a,b]에 존재하는 모든 수의 합을 구하라고 한다면 어떻게 구할 수 있을까?
가장 쉬운 방법은, 그냥 반복문으로 [a,b]까지 돌아서 모든 수의 누적합을 구하면 된다
answer = 0
for i in range(a,b+1):
answer += A[i]
만약 배열 A의 크기가 N일때, 최악의 경우 위 코드의 시간 복잡도는 O(N)이다. 1번부터 N번까지 다 더하라하면 O(N)이니까
여기까지는 괜찮은데 만약 이러한 질문을 M번이나 한다면?
O(N)의 연산을 M번 수행해야하므로, 시간복잡도는 O(NM)이고 N,M이 매우 크다면, 당연히 매우 느리다
2. Prefix sum
만약 S[0] = 0이고, 1번부터 i번까지의 수열 A의 합을 S[i]라고 정의한다면...
즉 S[i] = A[1] + A[2] + ... + A[i], S[0] = 0이면..
[a,b]에 존재하는 모든 수의 합은 어떻게 구할 수 있을까?
S[b] = A[1] + A[2] + A[3] + ... + A[b]
S[a] = A[1] + A[2] + ... + A[a] 이므로
A[a] + A[a+1] + A[a+2] + ... A[b] = S[b] - S[a-1]로 구할 수 있다
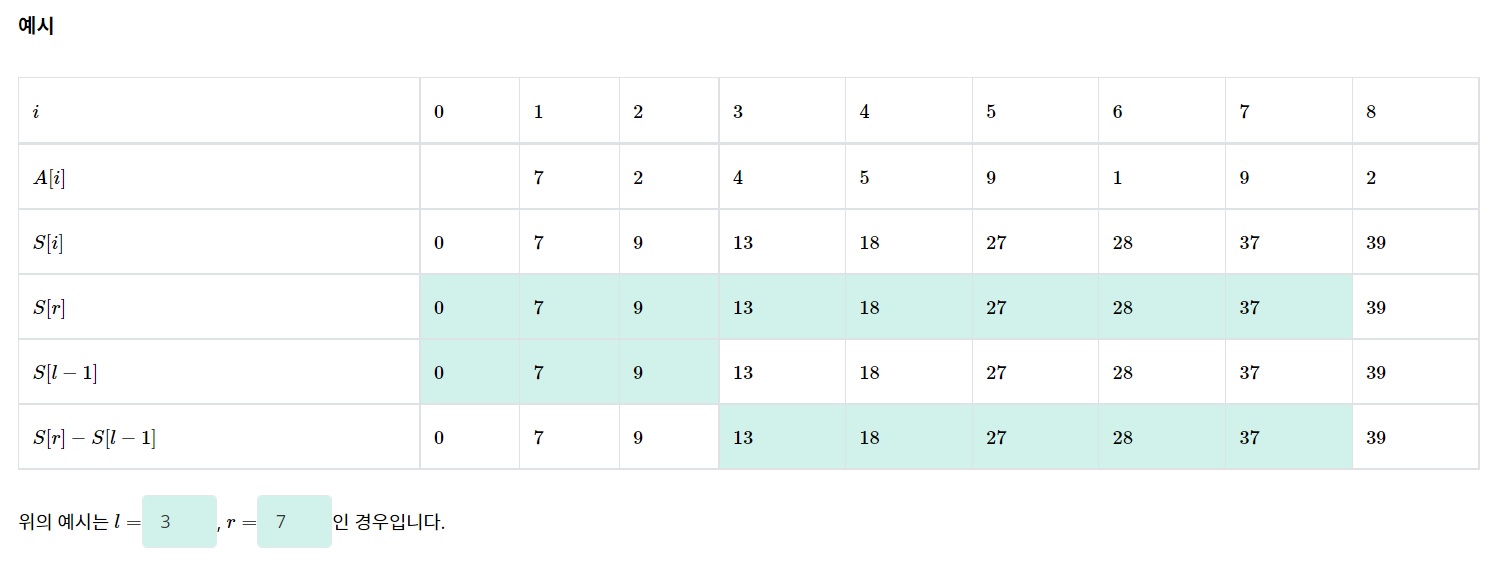
따라서 S[i]를 i=1,2,...에 대해 모두 구해놓은다면, 모든 구간의 누적합을 O(1)만에 구할 수 있다
2-1) 예시 문제
11659번: 구간 합 구하기 4 (acmicpc.net)
11659번: 구간 합 구하기 4
첫째 줄에 수의 개수 N과 합을 구해야 하는 횟수 M이 주어진다. 둘째 줄에는 N개의 수가 주어진다. 수는 1,000보다 작거나 같은 자연수이다. 셋째 줄부터 M개의 줄에는 합을 구해야 하는 구간 i와 j
www.acmicpc.net
누적합 배열을 구하고, 구간별로 구하면 되는데... 인덱스에 주의해야함
from sys import stdin
n,m = map(int,stdin.readline().split())
A = [0] + list(map(int,stdin.readline().split()))
s = [0]*(n+1)
for i in range(1,n+1):
s[i] = A[i] + s[i-1]
#A를 누적합 배열로 변경하고 싶다면..
#for i in range(1,n+1):
#A[i] += A[i-1]
for _ in range(m):
i,j = map(int,stdin.readline().split())
print(s[j] - s[i-1])
#A를 누적합 배열로 바꿨을경우
#print(A[j] - A[i-1])
3. Prefix sum의 한계점
이번엔 배열 A에서 i번째 수를 v로 바꿀때, [a,b]의 구간 합을 구하라고 묻는다면?
누적합 배열을 구한다는 것은 배열 A가 변경되지 않는다는 것을 전제로 하는 것이다
배열 A의 일부가 바뀐다면, 누적합 배열을 다시 구해야하므로 구간합을 구하는 것이 O(1)이 아니라 O(N)이 된다
따라서 물어보는 질문의 수가 매우 많다면 시간복잡도 O(NM)이 매우 커져서 문제가 된다
4. 세그먼트 트리(segment tree)
특정 구간의 결과값을 구하는데 사용하는 자료구조
여기서 말하는 결과값은 합도 있지만 곱, 최댓값, 최솟값, 최대공약수, 길이 등등도 가능하다.
------------------------------------------------------------------------------------------------------------------
편의상 결과값이 합이라고 생각하고 내용을 이어나가자.
1) 이진트리로 구성되어 있다.
2) 최상단 루트 노드는 전체 수열의 합을 저장하고
3) 각각의 노드는 특정 구간의 합을 저장한다
4) 부모 노드는 왼쪽 자식 노드와 오른쪽 자식노드의 합을 저장한다.
5) 각 자식노드는 부모 노드의 구간의 절반의 합을 저장하고 있다.
이렇게하면, 리프노드는 왼쪽부터 배열의 수 자체를 나타내고 리프노드가 아닌 노드들은 왼쪽 자식과 오른쪽 자식의 합을 저장하고 있다

여기서 x-y는 [x,y]의 합을 나타내고, x는 배열의 x번째 수를 나타낸다
5. 이진트리(binary tree)
잠깐 이진트리의 종류에 대해 알아보고 가자
5-1) full binary tree(proper, plane, strict binary tree)는 모든 노드의 자식 노드가 0개 이거나 2개인 경우인 이진트리를 말한다.
그러니까 자식 노드가 1개인 노드는 존재하지 않는 이진트리이다.

5-2) complete binary tree(완전 이진트리)는 마지막 레벨을 제외한 모든 레벨 h=0,1,2,...에 대하여 $2^{h}$개의 노드를 모두 가지고 있어야하며 마지막 레벨에서 노드들은 모두 왼쪽에 몰려있어야한다.
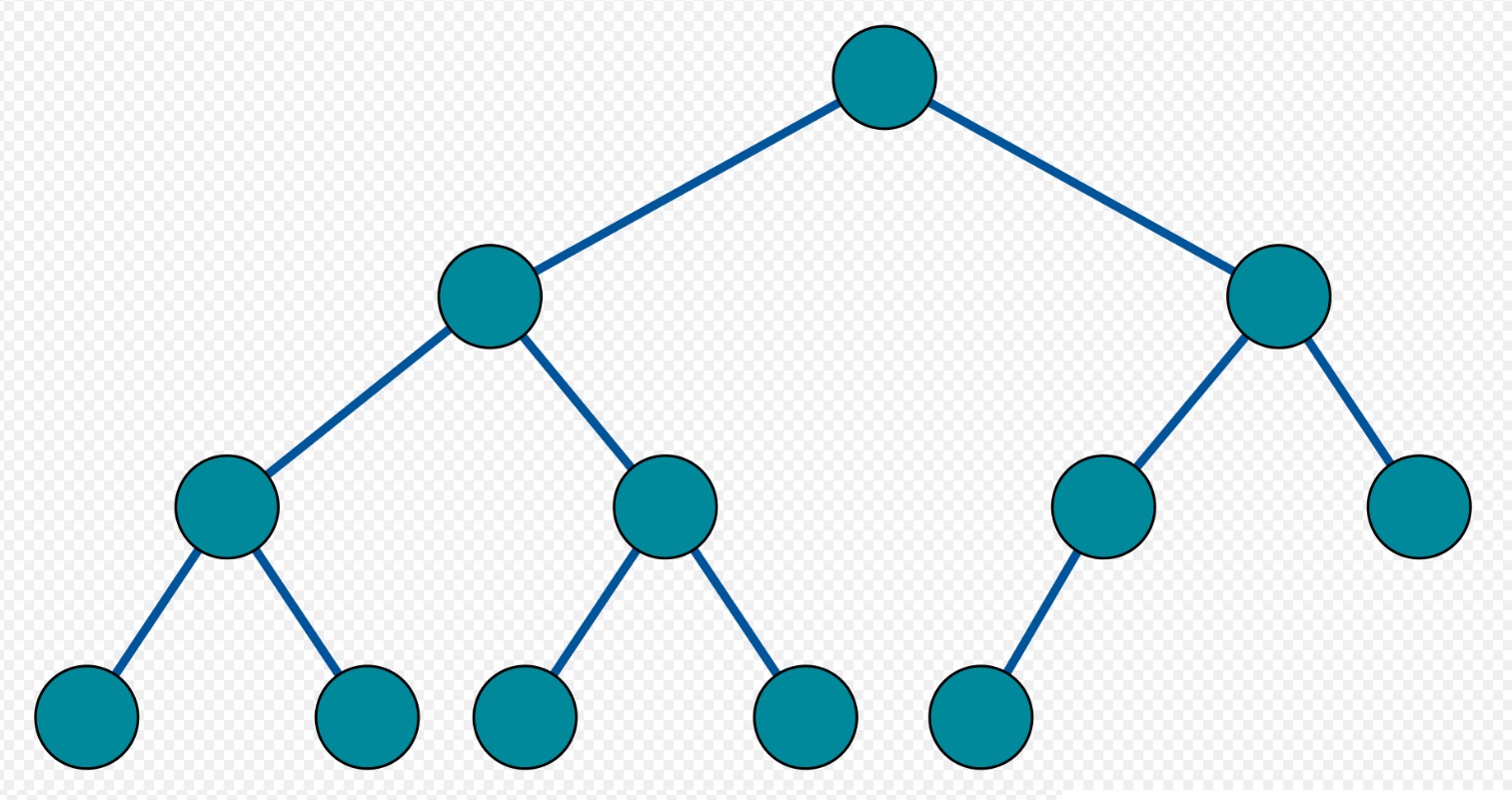
5-3) perfect binary tree(포화 이진트리)는 모든 노드가 2개의 자식 노드를 가진다.

6. 세그먼트 트리의 성질
6-1) 세그먼트 트리는 리프 노드를 제외한 모든 노드가 2개의 자식 노드를 가지는 Full binary tree이다.
왜 그런지 생각해보면.. 그냥 최소의 경우를 생각해보면 간단하다
최소는 배열의 수가 1개일때, 2개일때 생각해보면

배열의 수가 1개있으면... 그냥 노드가 1개있는 이진트리이고 배열의 수가 2개있으면 루트노드 1개에 자식노드가 2개 달린 이진트리이고..
수가 3개 있으면.. 이런 느낌일려나..? 아무튼 항상 자식노드가 2개이거나 0개인 이진트리가 되는데

6-2) 배열의 크기 N이 2의 거듭제곱꼴이라면, Perfect binary tree가 된다.
몇개만 해보면 느낌이 오겠지 뭐

만약 N이 $2^{h}$라고 한다면..? 왼쪽 자식이 $2^{h-1}$ 오른쪽 자식이 $2^{h-1}$로 나눠가지고...
다시 $2^{h-1}$이 $2^{h-2}$, $2^{h-2}$로 나뉘고...
다시 $2^{h-2}$가 $2^{h-3}$, $2^{h-3}$으로 나뉘고...
결국에 $2^{1}$이 $2^{0}$, $2^{0}$으로 나뉘니까...
항상 perfect binary tree가 되는게 맞다
6-3) 배열의 크기가 N일때, 리프노드의 수는 당연히 N개인데 리프노드가 아닌 노드의 수는 N-1개가 된다??
역시 바로 감이 안오면.. N=1부터 그려보면 될 것같다

그려보니까 맞는것 같네..? 당연한건가??
perfect binary tree의 전체 노드의 개수가 n개이고 리프 노드의 개수가 x개라고 한다면...

n-x는 어떻게 구할까? 위 그림에서 1+2+4와 같은데...
$\sum_{k=0}^{log_{2}x - 1} 2^{k}$
와 같이 구할 수 있을 것 같다
그런데 초항이 1이고 항의 수가 $log_{2}x$개이고 공비가 2인 등비수열의 합과 같으므로,
$$\sum_{k=0}^{log_{2}x - 1} 2^{k} = \frac{2^{log_{2}x} - 1}{2-1}$$
으로 구해진다.
그러므로 $n-x = x-1$
따라서 perfect binary tree에서 리프노드의 개수가 x개이면, 리프노드가 아닌 노드의 수는 x-1개이다.
full binary tree는 자식 노드가 0개이거나 2개이고,
그래서 perfect binary tree에서 리프노드를 2의 배수 꼴로 제거한 트리라고 생각할 수 있다
perfect binary tree에서 리프노드 2개를 제거하면, 리프노드가 아닌 노드 1개가 리프노드로 바뀌면서..
리프노드와 리프노드가 아닌 노드의 수가 1개씩 줄어든다
그래서 리프노드의 개수가 x-1개가 되고 리프노드가 아닌 노드의 수가 x-2개가 된다
그러니까 항상, 리프노드가 아닌 노드의 수는 리프노드의 개수-1이 된다.
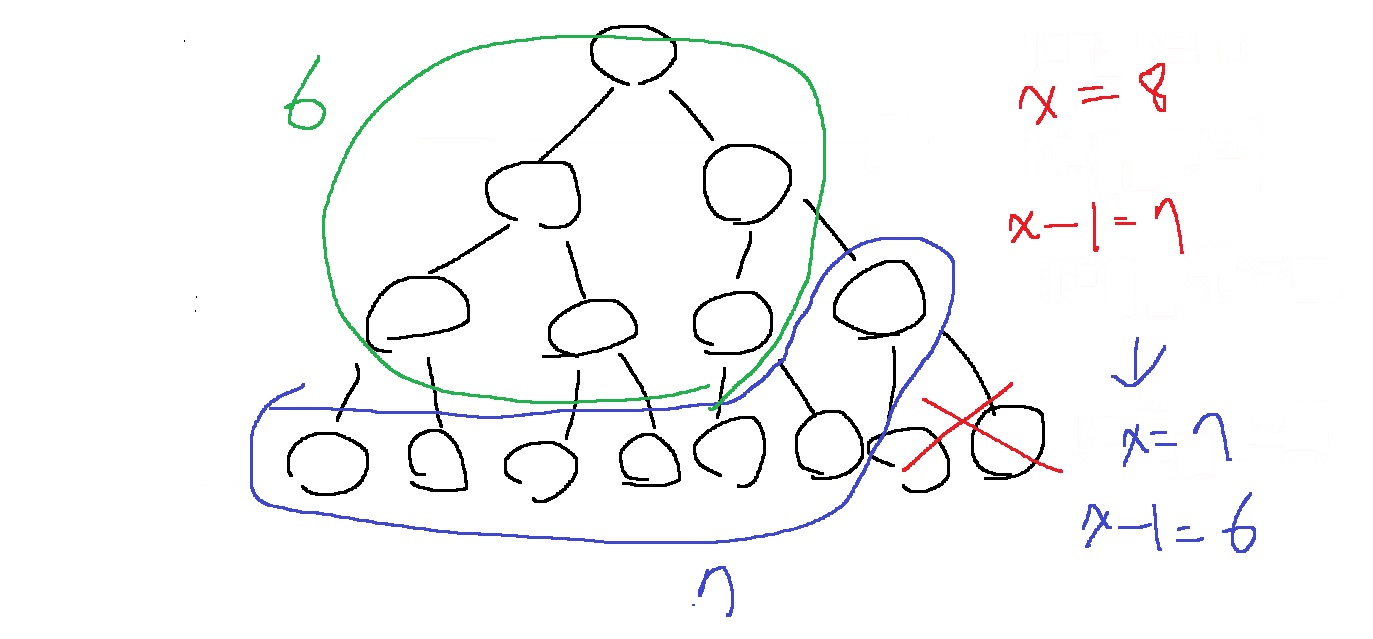
그러니까 리프노드 4개를 제거하면... 리프노드의 수는 x-2가 되고 리프노드가 아닌 노드의 수는 x-3이 된다는 말
그래서 리프노드 2a개를 제거하면? 리프노드의 수가 x-a가 되고 리프노드가 아닌 노드의 수는 x-a-1이 된다는 말
6-4) 그러므로 배열의 크기가 N일때, 세그먼트 트리에서 필요한 노드의 수는 2N-1개가 된다.
참조
누적 합
배열의 시작 인덱스위의 설명에서 배열 $A$의 시작 인덱스는 $1$로 사용했습니다. 그 이유는 $S[l-1]$ 때문입니다. 시작 인덱스가 $1$이면 $l$의 최솟값은 $1$이고, 여기서 $l-1$은 $0$입니다. 만약, 시작
book.acmicpc.net
세그먼트 트리
누적 합을 사용하면, 1번 연산의 시간 복잡도를 $O(1)$로 줄일 수 있습니다. 하지만, 2번 연산으로 수가 변경될 때마다 누적 합을 다시 구해야 하기 때문에, 2번 연산의 시간 복잡도는 $O(N)$입니다.
book.acmicpc.net
Binary tree - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Limited form of tree data structure Not to be confused with B-tree. A labeled binary tree of size 9 and height 3, with a root node whose value is 1. The above tree is unbalanced and no
en.wikipedia.org
이진트리의 종류에 대하여 (오류 수정) | Digital Dynamics (ddmix.blogspot.com)
이진트리의 종류에 대하여 (오류 수정)
클린 에너지 확대/지구 온난화 저지에 힘을 보탭니다.
ddmix.blogspot.com
41. 세그먼트 트리(Segment Tree) : 네이버 블로그 (naver.com)
41. 세그먼트 트리(Segment Tree)
이번 시간에 다룰 내용은 여러 개의 데이터가 연속적으로 존재할 때 특정한 범위의 데이터의 합을 구하는 ...
blog.naver.com
'알고리즘 > 세그먼트 트리' 카테고리의 다른 글
| 파이썬 알고리즘 기본기 곱셈 연산에서 주의할 점 배우기(세그먼트 트리 문제) (0) | 2022.12.10 |
|---|---|
| 세그먼트 트리 응용2 -최솟값과 최댓값을 구하는 세그먼트 트리- (0) | 2022.12.08 |
| 세그먼트 트리 응용1 - 구간의 곱을 구하는 세그먼트 트리 (0) | 2022.12.06 |
| 고난이도 자료구조 세그먼트 트리 구현하면서 이해하기 3편(값을 업데이트 하는 방법) (0) | 2022.12.05 |
| 고난이도 자료구조 세그먼트 트리 구현하면서 이해하기 2편(생성하고 합을 구하는 방법) (0) | 2022.12.05 |

