1. Huber loss
MSE와 MAE가 모두 바람직하지 않은 경우도 많다.
만약 90%의 데이터가 매우 큰 값 예를 들어 200,
10% 데이터가 0~10정도 값을 가진다고 하면
MSE는 10%의 작은 값을 가지는 0~10에 맞출려고 하고 MAE는 90%의 데이터가 있는 200에 맞출려고 한다.
MSE는 식 자체가 평균을 구하는 것에 목적이 있고 MAE는 중앙값을 구하는 것에 목적이 있다.
수학적으로 MSE를 가장 최소화하는 하나의 예측치는 평균이고, MAE를 가장 최소화하는 하나의 예측치는 중앙값이다.
이런 경우 적합한 loss function은 huber loss라고 있다.

huber loss는 MSE와 MAE를 적절하게 합친 것이다.
그래서 MSE에 비해 outlier에 덜 민감하고 MAE에 비해 gradient 문제에 덜 민감하다
그런데 hyperparameter인 $\delta$를 따로 학습해야하는 문제가 있다.
2. KL divergence
true distribution이 P라 하고 P가 따를 것 같다고 생각하는 우리가 예측한 모형의 확률분포가 Q라고 한다면
$$D _{KL} (P||Q)=H(P,Q)-H(P)$$
$H(P,Q)$는 P와 Q의 cross entropy이고 $H(P)$는 p의 entropy이다.
p대신에 q를 사용하여서 잃어버리는 정보량의 차이를 계산한다.
이게 0에 가까울수록 정답인 P대신에 Q를 사용해도 잃어버리는 정보량이 줄어든다는 의미이므로 하나의 loss로 사용할 수 있다
3. loss function의 선택
loss function은 성질에 따라 적절하게 선택해야함
MSE는 outlier가 매우 크면 제곱값이 매우 커져서 학습이 잘 안된다
그것의 대안으로 L1 norm인 절댓값 오차 합을 구하기도 한다
classfication의 cross entropy는 특징이 정답값과 로짓의 곱으로 나타난다
정답값은 보통 one hot vector로 클래스의 원소만 1
나머지는 0이기 때문에 로짓도 해당하는 부분만 높으면 충분하다
무슨말이냐면 그 값이 10이든 100이든 얼마이든 그냥 다른 값들보다 크기만 하면 충분하다
그것이 정말로 항상 좋은 loss인가? 고민해봐야할 문제다.
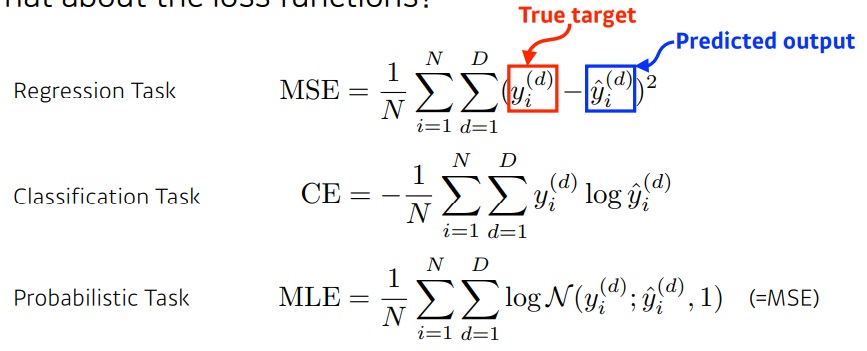
지금까지 여러가지 loss function에 대해 알아봤지만 모든 문제를 설명해주는 단 하나의 loss function은 존재하지 않는다.
문제 상황부터 무슨 알고리즘을 선택했는지, 데이터 상태는 어떤지, loss function의 미분은 가능한지 여러 가지를 고려하여 선택한다.
loss function을 어떤 것을 선택하느냐에 따라 학습에 분명 차이가 있다.
예를 들어 outlier가 있는 경우 모형 성능이 좋더라도 MSE를 쓰면 학습이 잘 안될 것이다.
4. 참고
5 Regression Loss Functions All Machine Learners Should Know
Choosing the right loss function for fitting a model
heartbeat.comet.ml
'딥러닝 > 딥러닝 기초' 카테고리의 다른 글
| L1 regularization(Lasso)과 L2 regularization(Ridge) (0) | 2021.12.15 |
|---|---|
| regularization이란 무엇일까? (0) | 2021.12.15 |
| MSE loss 와 MAE loss의 비교 (0) | 2021.11.22 |
| cross entropy loss(=log loss)에 대한 고찰 (0) | 2021.11.20 |
| loss function에 대하여 (0) | 2021.11.19 |

