1. 비트(bit)
정보를 구분하는 최소 단위로 이진 숫자(binary)를 뜻한다
0,1의 값을 가지며 True/False나 on/off같은 2가지 상태를 나타낼 수 있다
10진수를 2진수로 바꾸면 해당 10진수에 대응하는 하나의 비트열을 얻는다

2. 비트연산
- 비트연산은 비트열의 같은 위치끼리만 연산함
2-1) &(and)
비트 단위로 and연산을 수행
비트가 둘다 1이면 1이고, 하나라도 0이면 0인 연산
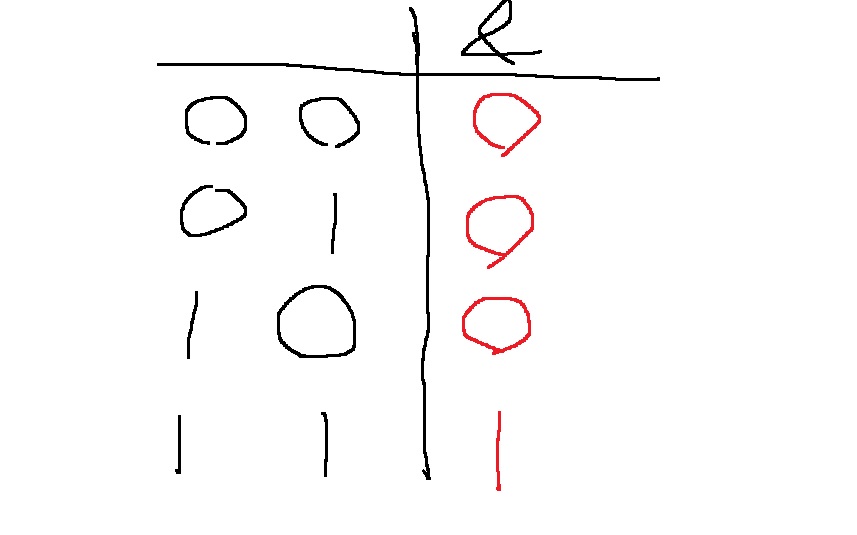
& 연산은 위 표에서 특징을 자세히 살펴보면..
1) 0과 and연산은 무조건 결과가 0이다
0&0 = 0
0&1 = 0
2) 1과 and연산은 나머지 비트를 그대로 가져온다
1&1 = 1
1&0 = 0
2가지 성질을 잘 이용하면..
3) 어떤 비트열에서, 특정 부분을 0으로 만들고 싶다면..
나머지는 1과 연산하고 그 부분만 0과 연산시키면 특정 부분을 0으로 만든 비트열을 얻는다

4) 특정 비트가 1인지, 0인지 검사하고 싶다면?
1과 &연산을 수행하면 해당 비트를 그대로 가져오므로
해당 특정 비트의 위치에는 1 나머지는 0으로 만든 비트열과 &연산을 수행
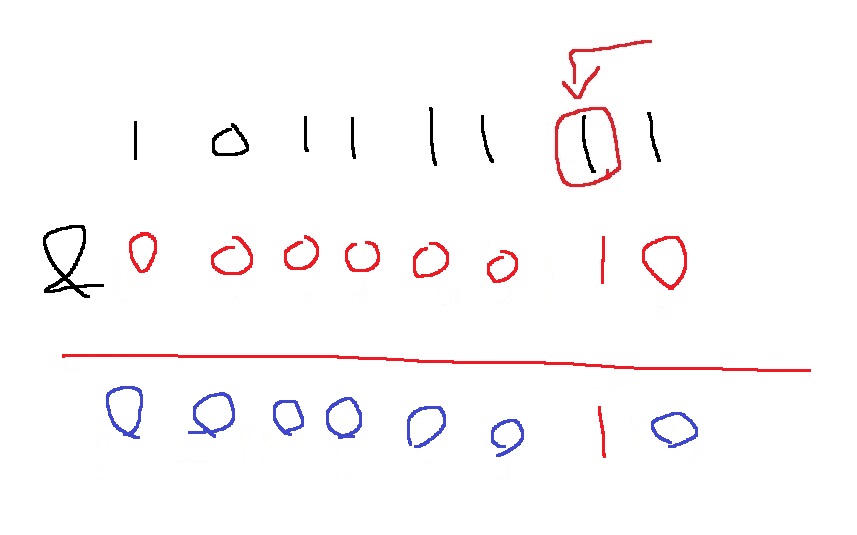
예시)

2-2) | (or)
비트 단위로 or연산을 수행함
두 비트가 모두 0이면 결과가 0이고, 그렇지 않으면 1인 연산
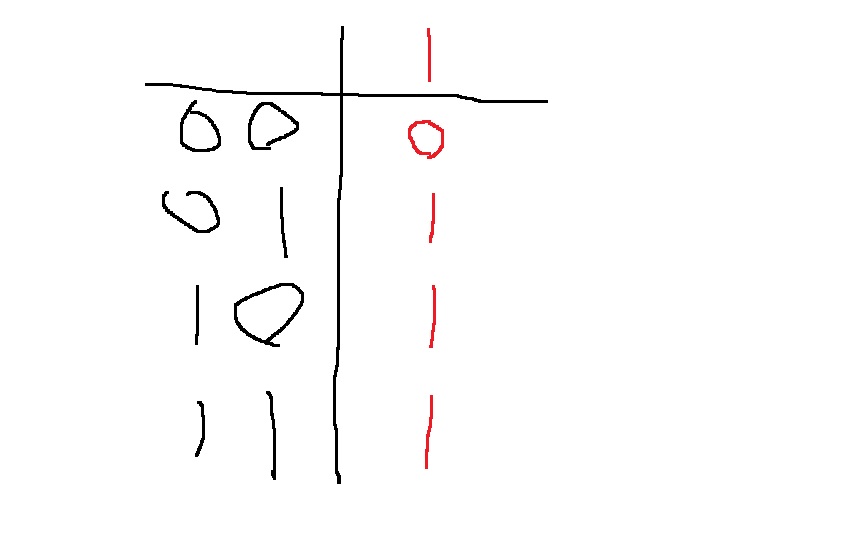
위 표를 자세히 살펴보면 | 연산의 특징을 발견할 수 있다
1) 0과 | 연산을 수행하면, 그 비트를 그대로 가져온다
0 | 0 = 0
0 | 1 = 1
2) 1과 | 연산을 수행하면 1을 가져온다.. 비트가 1로 바뀐다
1 | 0 = 1
1 | 1 = 1
특정 비트만 1로 만들고 싶다면... 나머지는 0으로 하고 그 부분만 1로 만든 비트열과 | 연산을 수행하면 될 것이다

예시)

2-3) ^(XOR)
비트 단위로 XOR 연산을 수행함
XOR연산은 둘이 같으면 0이고 다르면 1인 연산이다
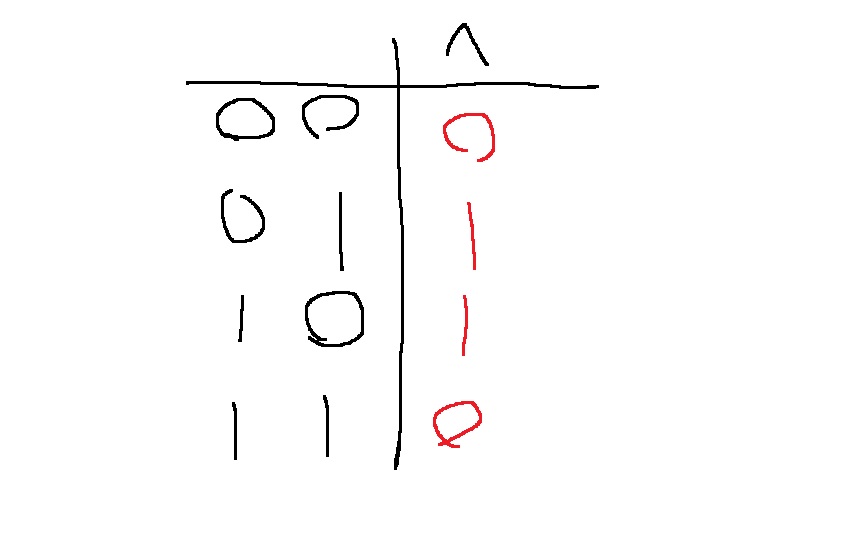
특징을 자세히 살펴보면..
0과 xor연산을 수행하면 그대로 가져오는데..
1) 1과 XOR연산을 수행하면 해당 비트가 반대로 된다.
0 ^ 1 = 1
1 ^ 1 = 0
bit = bit^1이라고 쓰면 이해할 수 있나?
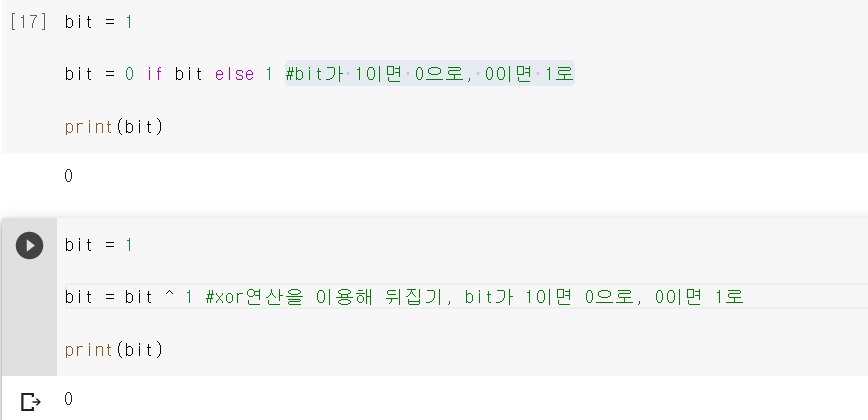
예시)

0011인데.. 앞에 0은 지우는게 기본이다보니..
2-4) ~(not)
해당 비트열의 모든 비트를 반전 시킨다
0은 1로, 1은 0으로
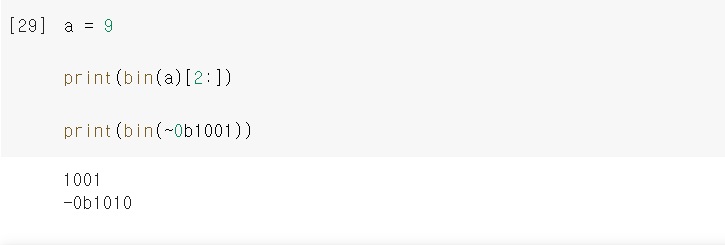
파이썬으로 계산해보면.. 예상하는 결과인 0110과는 조금 다른데
순수한 비트연산이 아니고 정수 비트연산을 해서 그렇다고는 하네
파이썬 비트연산자 사용법 정리 (Python 비트연산) (withcoding.com)
파이썬 비트연산자 사용법 정리 (Python 비트연산)
라즈베리파이 같은 하드웨어가 인기를 끌면서 (C언어 만큼은 아니지만) 파이썬으로 하드웨어를 제어하는 경우가 늘어나고 있습니다. 하드웨어 쉽게 제어하기 위해서는 비트연산자를 잘 사용할
withcoding.com
파이썬에서 음수 저장 + 비트에 대한 보수 연산때문에 ~x는 -(x+1)과 동일하다고함
BitwiseOperators - Python Wiki
BitwiseOperators - Python Wiki
FAQ: What do the operators <<, >>, &, |, ~, and ^ do? These are Python's bitwise operators. Preamble: Twos-Complement Numbers All of these operators share something in common -- they are "bitwise" operators. That is, they operate on numbers (normally), but
wiki.python.org
2-5) <<
a << n하면 비트열 a를 왼쪽으로 n칸 이동시킨다
움직이는건 비트 1을 움직인다고 생각하면 된다
움직이고 나서 나머지는 모두 0으로 채운다
1이 움직이다가 왼쪽으로 자리를 벗어나면 비트열 길이가 그만큼 늘어남

이진수 연산과 연관시켜서 생각을 해보면 특징이 있는데
비트열 1의 자리는 1이고, 10의 자리는 2이고, 100의 자리는 4이고, 1000의 자리는 8이잖어...
n번째 자리는 $2^{n}$을 나타내니까..
0001 << 1을 하면, 0010 = 2
0001 << 2를 하면 0100 = 4
0001 << 3을 하면 1000 = 8
...
왼쪽으로 1칸씩 옮기면 2가 곱해진다는 특징이 있다
그래서 a << n은 $a\times 2^{n}$과 같다
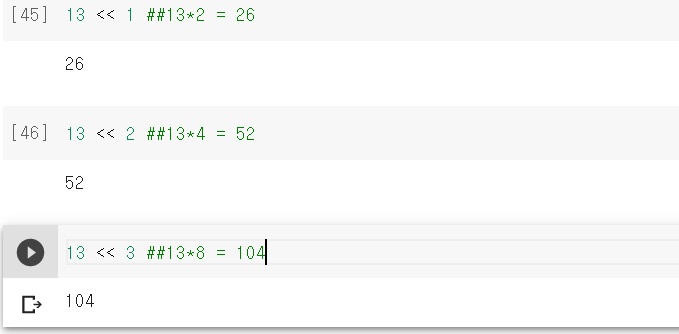
2-6) >>
a >> n하면 비트열 a를 오른쪽으로 n칸 만큼 옮긴다
<<과 마찬가지로 움직이는건 비트 1이고, 나머지는 모두 0으로 채움
<<과는 다르게 1이 오른쪽으로 벗어나버리면, 그 1은 없어진다

앞에 0은 지워지니까 표시 안했어
마찬가지로 << 처럼 >>을 수행하면, n번째 자리가 n-1번째 자리로 이동하잖아
그러므로, a >> n을 수행하면 $a // 2^{n}$과 같다

3. 비트 연산 응용
정수 1은 "비트가 켜져있다", 정수 0은 "비트가 꺼져있다"라고도 표현한다
3-1) 1 << n은 "n번째 비트를 켠다"라는 의미를 가진다
아주 심플하게 1은 이진수로 나타내면 0000000000000000000000...00001로 0번째 비트가 켜져있다는 의미이고
이것을 n만큼 왼쪽으로 옮기는 << n 연산을 수행하면...
n번째 비트가 1이 되므로, n번째 비트가 켜져있다는 뜻이 된다

참고로 비트가 켜진 위치는 0번부터 세는 것이다. 3번 비트가 켜져있다는 뜻은, '100'이 아니라, '1000'이다
이를 활용한 대표적인 예제는 부분집합을 만들 때 사용했었다.
어떤 정수 i의 n번째 비트가 켜져있는지, 꺼져있는지를 알고싶다면..
def examine_nth_bit(i,n):
return 1 if i & (1<<n) else 0
"정수 i의 n번째 비트가 켜져있으면 1, 꺼져있으면 0을 반환"

만약 다음과 같이 작성하면 어떨까?
def examine_nth_bit(i,n):
return i & (1<<n)
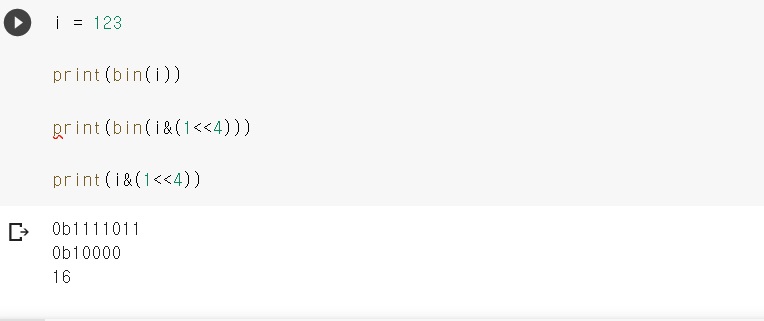
이는 정수 i를 2진수로 나타낸 것과 1<<n을 비트연산한 결과를 10진수 형태로 반환하는 것이다
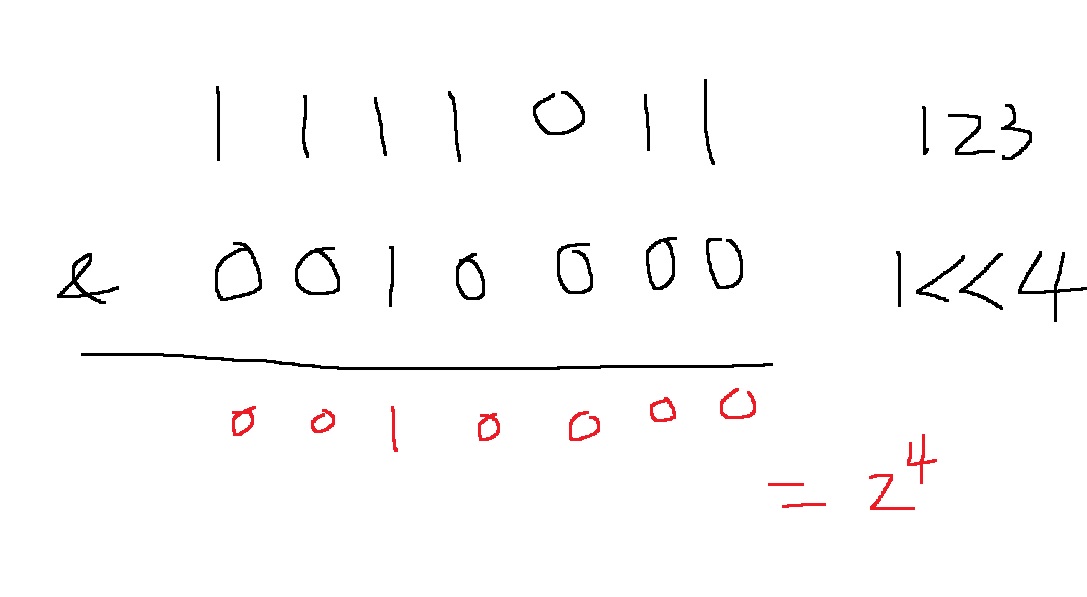
123을 2진수로 나타내면 1111011이고, 1<<4는 0010000이고, 이것을 &연산을 수행하면, 0010000이다.
이것은 16이다
실제로 결과도 16이 나온다
당연하지만 n번째 비트가 0이라면, 00000000이 나올 것이므로 결과도 0이다.
그래서 i & (1<<n)은 정수 i의 n번째 비트가 꺼져있다면 0을 반환하지만, 켜져있다면 n번째 비트만 켜진 정수를 반환한다

3-2) "(1<<n) - 1"은 n개의 비트를 모두 켠다
단지 1을 뺐는데 n번째 비트를 켜는 것에서, n개의 비트를 모두 켜는 것으로 식의 의미가 완전히 바뀐다

사실 생각해보면 매우 당연한 결과인데
예를 들어 10진수에서 사용할 수 있는 숫자는 0~9인데, 5자리 최소의 10진수 10000에서 1을 빼면, 4자리 가득찬 9999가 나오듯이
1<<4는 5자리 최소의 2진수 10000에서 1을 빼면... 2진수는 0~1까지 사용가능하잖아..
5자리 최솟값에서 1을 뺐으니 4자리 가득찬 1111이 나오는 것은 어찌보면 당연하다
4. 비트마스킹(bitmasking)
컴퓨터는 모든 자료를 이진수로 표현하기때문에, 이러한 특성을 이용해서 정수의 이진수 표현을 하나의 자료구조로 활용하는 테크닉이다
어떤 숫자에, 마스크라고 불리는 어떤 비트열을 비트연산해서, 그 숫자의 특정 비트부분을 가져오거나, 변경시키고 싶을 경우에 사용하는 테크닉
비트마스킹 기법을 사용하는 이유는 일반적으로 원소의 수가 적을때 수행시간이 빨라지고, 메모리 사용량이 더 적은 점이 있다
코드가 간결해지기는 하는데 이해하고 있지 못하면 알아먹기 어려울 수 있다
-----------------------------------------------------------------------------------------------------------------------
예를 들어, 39925에서 특정 부분의 비트열을 가지고 오고 싶다면..?
39925가 2진수로 바꾸면 1001 1011 1111 0101인데..
5~8번 부분만 가지고 오고 싶다면 그 부분만 1로 하고 나머지는 0으로 한 비트열과 &연산을 수행하면 될 것
0000 0000 1111 0000와 &연산을 수행
마지막 비트 4자리만 가지고 오고 싶다면?
4자리 비트를 모두 켜는 연산 ((1<<4)-1)은 0000 0000 0000 1111이잖아
이것과 &연산을 수행하면 될 것이다

4-1) 정수 i를 이진수로 바꿀 때, 1의 개수는?
정수 i를 이진수로 바꿔서, 나온 비트열의 길이가 k라고 한다면, 0~k-1까지 비트 각각이 1인지 아닌지를 검사해서
비트가 1이면 counting을 한다
1 << n은 n번째 비트를 켠 비트열이므로 위에서 이미 보인대로 i & (1<<n)이 0인지, 0이 아닌지 조사하면 될 것이다
n = 234
print(bin(234))
b_n = len(bin(234)[2:])
cnt = 0
for k in range(b_n):
if n & (1<<k) != 0: ##비트가 켜져있다
cnt += 1
print(cnt)
"""
0b11101010
5
"""
근데 사실 길이를 안구해도 다음과 같이 구할수도 있다
k를 계속 증가시키면서, 1<<k가 n보다 커지면 반복을 멈추는 것
n = 234
print(bin(234))
cnt = 0
k = 0
while n >= 1<<k:
if n & (1<<k) != 0:
cnt += 1
k += 1
print(cnt)
"""
0b11101010
5
"""
4-2) 정수 n을 2의 지수승으로 표현할 수 있는지의 여부
n이 2의 지수승으로 표현할 수 있다면, n을 이진수로 바꿀 때 맨 앞자리 비트는 1이고 나머지는 0이다
1000000000000...000000
이 비트열에 1을 빼면, 즉 n-1은 n개가 전부 1인 비트열로 바뀐다는 것을 위에서 보였다
01111111111111...111111
두 비트열을 &연산을 수행하면 0이 될 것이다
따라서.. n & (n-1)이 0이라면 n은 2의 지수승으로 표현할 수 있다

4-3) boolean값 바꾸기
위에서 이미 보인 것이긴 하지만, xor연산자는 어떤 비트를 비트 1과 xor연산을 하면 비트가 반전된다고 했다
그래서 1 ^ 1 = 0 이고 0 ^ 1 = 1이다.
이를 이용하면.. 원래 True인 것을 False로 바꾸고 False인 것을 True로 바꿀 수 있다

일반적으로 위와 같이 쓰지만 xor연산을 이용하면 더욱 간단해진다
onoff = True
onoff ^= True
print(onoff)
"""
False
"""
5. 집합으로의 응용
비트마스킹을 이용하는 가장 큰 이유중 하나는 집합 구조를 2진수로 표현할때 다양한 연산을 굉장히 빠르고 쉽게 수행할 수 있다는 점에 있다
5-1) 집합의 표현
원소의 개수가 n인 집합이 있다고 하자.
해당 집합을 비트열로 표현하는 방법은, 길이가 n인 비트열로 표현하면 된다
그러면 어떤 원소가 집합에 들어가있는 것은 어떻게 나타낼 수 있을까?
해당 위치의 비트가 1로 켜져있다면, 해당 위치의 원소는 집합에 포함되어있고, 비트가 0으로 꺼져있다면 해당 위치의 원소는 집합에 포함되어있는 것이 아니다.
만약 210을 2진수로 나타낸 1101 0010은 집합으로 나타내면 어떻게 나타낼 수 있을까?
1로 켜져있는 비트의 위치를 원소로 가지는 집합으로 나타내면 어떨까?
1101 0010은 1번째, 4번째, 6번째, 7번째 비트가 켜져있다. 그러므로
1101 0010 = {1,4,6,7}로 나타낼 수 있다
----------------------------------------------------------------------------------------------------------
혹은 다르게 생각해볼 수도 있다
집합이 {1,2,3,4,5,6,7}이라고 한다면, 1101000은 무엇을 나타낼까..?
대응하는 위치의 원소를 집합에 포함시키면 된다. 1101000 = {1,2,4}
{3}은 어떻게 나타내면 좋을까? 0010000
-------------------------------------------------------------------------------------------------------
이런 식으로 해당 위치의 원소가 포함되어있다, 포함되어있지 않다를 나타내는 boolean 배열
[True, True, False, True, False, False, False] = {1,2,4}로 나타내야하는 것을
104 = 1101000의 정수 하나로 나타낼 수 있어서 메모리가 줄어든다
------------------------------------------------------------------------------------------------------
5-2) 집합에 원소를 추가하는 방법
1101000 = {1,2,4}라는 집합에 원소 3을 추가시키고 싶다면 어떻게 가능할까?
{1,2,3,4}는 1111000으로 나타낼 수 있는데, 1101000에서 4번째 비트를 1로 바꿔줘야한다.
그것은 | 연산을 이용하면 가능하다는 것을 보였다
어떤 비트를 1과 | 연산을 수행하면 1을 가져온다고 했다
따라서 1101000 | 0010000 = 1111000이므로...
1101000 | 1<<4를 수행하면 원소 3을 집합에 추가한 상태가 된다
현재 상태 a에서 위치 p(오른쪽에서)의 원소를 추가하고 싶다면..
a = a | 1<<p
위치 p는 문제에 따라 너가 생각을 잘 해야겠지..
5-3) 집합에서 특정 위치의 원소를 삭제하고 싶다면..?
1101000에서 4번째 원소를 추가해서, 1111000으로 바꿨는데... 추가한 원소를 다시 빼고싶다
그러면 1101000으로 바꿔야한다는 소리인데.. 어떻게 가능할까?
위에서 어떤 비트와 0과 &연산을 수행하면 0으로 되고 1과 &연산을 수행하면 그대로 가지고 온다고 했다
1 << 4는 0010000이다.
not연산인 ~연산은 비트 0을 1로 비트 1을 0으로 바꿔준다고 했다
~(1<<4)는 1101111이다.
이것과 1111000을 &연산을 수행한다면... 4번째 비트만 0으로 바꿔주고 나머지는 그대로 가지고오므로..
1111000 & ~(1<<4) = 1101000
일반적으로 집합 a에서 위치 p의 원소를 제거하고 싶다면...
a = a & ~(1<<p)
5-4) 원소의 토글
토글 연산은 p번째 비트를 0이면 1로 1이면 0으로 바꾸는 연산이다.
이미 위에서 xor연산으로 가능하다는 것을 보였다.
집합 a에서 p번째 위치의 원소가 있다면 삭제하고, 없다면 추가하는 연산은...
a = a ^ (1<<p)
5-5) 해당 위치에 원소가 존재하는가?
이것도 역시 이미 많이했다
p번째 위치에 원소가 존재하는지 아닌지는 p번째 위치의 비트가 1인지 아닌지를 검사하는 것과 같다
비트 1과 &연산을 하면 해당 비트를 그대로 가지고 오므로..
a & (1<<p)가 0이면 해당 위치의 비트는 0이고 원소가 존재하지 않는다
a & (1<<p)가 0이 아니면 원소가 존재한다..
또한 a & (1<<p)가 0이 아니면.. 1이 되는게 아니라 해당 위치값을 10진수로 바꾼 값을 반환한다는 것도 이미 위에서 보였다
5-6) 집합의 크기?
집합의 크기는 집합에 포함된 원소의 개수이다.
집합은 2진수 비트열로 표현될 수 있고, 포함된 원소는 1로 켜져있다
그러므로 2진수 비트열에서 비트 1의 개수를 세면 된다.
이미 위에서 어떻게 가능한지 보였다
비트 1과 &연산을 수행하면 해당 비트를 그대로 가지고 오므로...
k값을 0부터 증가시키면서, n & (1<<k)가 0이 아니면 counting하면 된다
1<<k가 n보다 커지면 반복문을 종료한다
n = 210
cnt = 0
k = 0
while n >= (1<<k):
if n & (1<<k) != 0:
cnt += 1
k += 1
print(cnt)
"""
4
"""
5-7) 두 집합에 대한 집합 연산
비트 연산 기호는 집합 연산 기호와 대응되는데 &연산은 교집합이고 | 연산은 합집합이다

차집합은 어떻게 가능할까?
단순히 a-b를 해도 될까? - 연산이 비트연산과 대응되지 않아서 그대로 사용하면 안된다
하지만 &&A-B = A\cap B^{c}$$와 같다는 사실은 유명하다
여집합은 정확히 비트 연산에서 not 연산 ~과 대응된다
여집합은 어떤 집합이 가지는 원소를 포함하지 않는 집합을 의미하기 때문이다
print(bin(0b1100011 & ~(0b0110101))) #차집합
"""
0b1000010
"""
집합 A = 1100011이고 집합 B=0110101이면, A-B는 A에는 포함되는데 B에는 포함되지 않는 원소들로 이루어진 집합이다
그러므로 1000010이 나와야한다. 실제로 위 결과도 일치한다
대칭차집합은 어떨까?
A와 B중 하나에만 포함된 원소들의 집합을 A와 B의 대칭차집합이라 하고 다음과 같이 표현된다
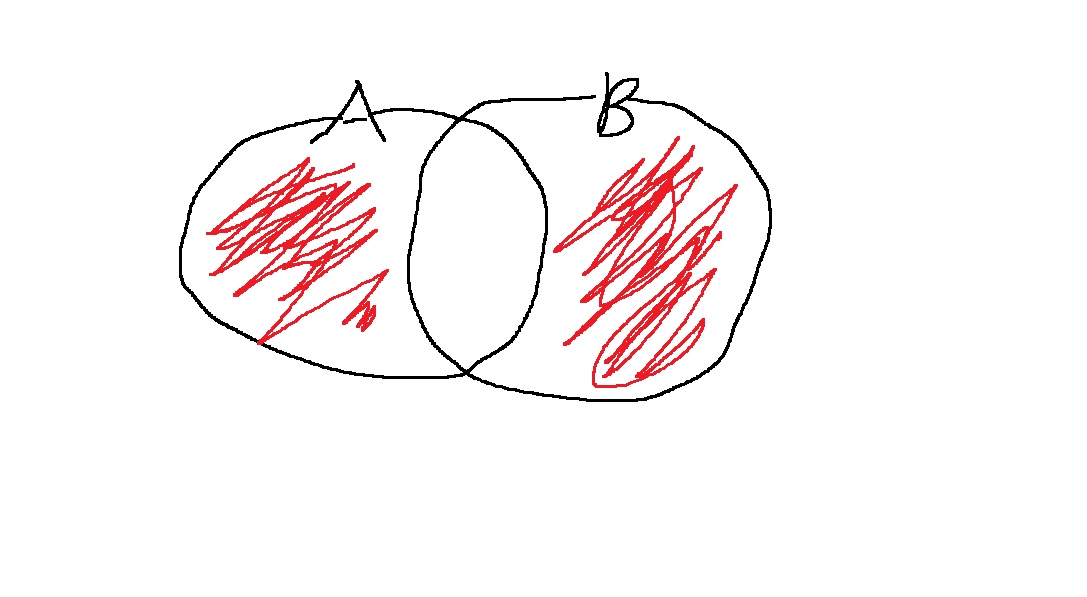
XOR 연산은 두 비트가 다르다면 1이고 비트가 같다면 0이다
따라서 A ^ B를 이용하면 대칭차집합이 나올 것이다
print(bin(0b1100011 ^ 0b0110101)) #대칭차집합
"""
0b1010110
"""
A = 1100011이고 B=0110101이면.. A와 B모두에 포함되는 원소는 제거해야한다
그러면 1010110이 나올 것이다. 실제로 위 결과도 일치한다
5-8) 모든 원소를 포함하는 집합과 공집합
모든 원소를 포함하는 집합은 n개의 비트가 모두 1일것이다.
위에서 n개의 비트를 모두 켤려면 (1<<n)-1이면 된다는 것을 보였다
공집합은 당연히 모든 비트가 0일때이다.
그러므로 공집합은 0으로 표현할 수 있고 모든 원소를 포함하는 집합은 (1<<n)-1이면 된다
5-9) 최하위 비트를 찾는 방법
음수가 보수를 이용하기 때문에 이를 이용하면 된다고 하는데
무슨말인지 모르겠으니까 그냥 외워
a & (-a)를 하면 최하위 비트를 찾을 수 있다
b = int('0110100',2)
print(bin(b & -b))
"""
0b100
"""
5-10) 최하위 비트를 제거하는 방법
어떤 수에 1을 빼면, 최하위 비트에서 내림이 되어서.. 그 나머지는 모두 1로 바꿔준다
그러니까 100000에서 1을 빼면 011111가 되듯이..
혹은 100100에서 1을 빼면 100011이 된다는 소리
그러면 100100과 100011을 &연산을 수행하면? 최하위 비트가 0이 된다

5-11) 모든 부분집합을 순회하는 방법?
널리 알려져있는 방법은..
근데 무슨 말인지 모르겠엌ㅋㅋㅋㅋㅋㅋㅋㅋ
(n-1) & n이 0이면 2의 지수승으로 나타낼 수 있고.. 그걸 이용한건가?
아니면 (n-1) & n이 최하위 비트 원소를 제거한거니까
원래 11은 1011이거든... 1011을 출력하고
먼저 1011에서 1을 빼면 1010인데 얘랑 원래 집합 1011의 교집합을 다음 subset으로 넘기고 출력하고
1010에서 다시 1을 빼면 1001인데.. 1011의 교집합을 구해서 subset으로 넘기고
다시 1001에서 1을 빼면 1000인데 교집합을 구해서 subset으로 넘기고
# 모든 부분집합 순회하기
sets = 11
subsets = 11
while True:
print(bin(subsets))
subsets = (subsets - 1) & sets
if subsets == 0:
print(bin(subsets))
break
"""
0b1011
0b1010
0b1001
0b1000
0b11
0b10
0b1
0b0
"""
여기까지 오면.. 그냥 subsets-1을 넘기면 되는거 아니야? 그럴수도 있는데
1000에서 1을 빼면 0111인데.. 0100은 실제 집합 1011에는 존재하지 않거든..
그래서 교집합을 구하는거네?
아무튼 1씩 빼서 원래 집합과 교집합을 구해서.. 0이되면 공집합이니까 공집합까지 출력하고 끝내면 된다
근데 내가 잘 아는 코드는
sets = [1,2,3]
n = len(sets)
for i in range(1<<n):
partial = []
for j in range(n):
if i & (1<<j):
partial.append(sets[j])
print(partial)
"""
[]
[1]
[2]
[1, 2]
[3]
[1, 3]
[2, 3]
[1, 2, 3]
"""
이게 더 직관적이긴해..
[알고리즘] 비트마스킹(bitmasking) 이란 :: 굳건하게 (tistory.com)
[알고리즘] 비트마스킹(bitmasking) 이란
안녕하세요, 여행벌입니다. 오늘은 2진수 표기법의 특징을 활용한 비트마스킹 알고리즘에 대해서 포스팅해보겠습니다. [ 비트마스킹 ] 컴퓨터는 내부적으로 모든 자료를 이진수로 표현합니다.
travelbeeee.tistory.com
현실에서 유용한 Bitwise 연산 및 활용 모음 - Parkito's on the way (shoark7.github.io)
현실에서 유용한 Bitwise 연산 및 활용 모음
개인적으로 알고리즘 문제와 실제 개발에서 유용하게 사용했던 몇몇 비트 연산 및 활용법을 소개합니다.
shoark7.github.io
비트마스크 (BitMask) 알고리즘 (rebro.kr)
비트마스크 (BitMask) 알고리즘
[목차] 1. 비트마스크(BitMask)란? 2. 비트마스크의 장점 3. 비트 연산자 4. 비트마스크를 이용한 집합 구현 * 종만북에 잘 설명되어 있어 기본적으로 종만북의 설명을 따릅니다. 1. 비트마스크(BitMask)
rebro.kr
16. 비트마스크 이용 팁
예시) 1 ~ 19까지 19개의 추가 서비스 목록 있다고 할 때 이를 간단하게 구현하는 방법 by 비트 마스크 20개의 모든 서비스를 받는다고 할 때 fullSerive = (1 << 20) - 1 원소 추가 # 2 번째 서비스를 받을것
goodsosbva.tistory.com
'알고리즘 > 비트마스킹' 카테고리의 다른 글
| 합과 bitwise or연산이 같게되는 조건 (0) | 2025.01.09 |
|---|---|
| 이진수의 마지막 n개의 비트가 모두 켜져있는지 확인하는 방법 (0) | 2024.05.03 |
| 비트마스크를 이용한 에라토스테네스의 체 배우기 (0) | 2023.05.04 |
| 정수 n을 2의 거듭제곱으로 나눈 나머지를 효율적으로 구하는 방법 (0) | 2023.05.03 |
| 비트마스킹 연습하기1(백준 25166,12833) (0) | 2022.10.30 |

