x+y = x | y를 만족하는 k번째로 작은 자연수 y를 구하는 문제
합과 or 연산이 서로 같게되는 조건을 먼저 생각해본다
or연산은 두 bit가 1이면 1이고 두 bit가 0이면 0이고 두 bit가 1,0으로 서로 다르면 1인 연산
두 수를 합하는 것은 어떤 의미인지 생각해본다
x,y를 2진수로 바꿔서 예를 들어 5 = 101이고 12 = 1100인데 이진수끼리 서로 덧셈은 어떻게 하는가?
$101 = 0 * 2^{3} + 1 * 2^{2} + 0 * 2^{1} + 1 * 2^{0}$
$1100 = 1*2^{3} + 1 * 2^{2} + 0 * 2^{1} + 0 * 2^{0}$
우측에 2의 거듭제곱으로 바꾼 것끼리 더한다고 생각해보면,
$(0 + 1)*2^{3} + (1+1)*2^{2} + (0+0)*2^{1} + (1+0)*2^{0}$
서로 같은 위치의 비트를 비교해서 0과 0이 만나면 0인데, 1과 0이 만나면 1이 되고
근데 1과 1이 만나면 그 다음 비트로 올림을 주는 거에서 bitwise or과 차이가 있음
일반적인 식 $a_{n}*2^{n} + a_{n-1}*2^{n-1} + .... + a_{0}*2^{0}$으로 해서 생각해봐도 위 관찰이 성립한다는 것을 알 수 있다
그러므로 x+y = x | y일려면 x,y를 2진수로 바꿨을때 같은 위치에 있는 비트들은 0,0이거나 1,0, 이거나 0,1이어야한다
예를 들어 2 = 10이고 5 = 101인데 7 = 111이고 10 | 101 = 111임을 알 수 있다
그러면 k번째로 작은 자연수를 어떻게 찾느냐가 문제인데 내가 처음에 풀었던건 뭔가 별로라서 버리고
다른 사람들이 어떻게 풀었는지 살펴보면 5 = 101을 예로 들어 생각해보자
101의 0번째 자리가 1인데 1과 만나면 안되니까 무조건 0이 와야하고
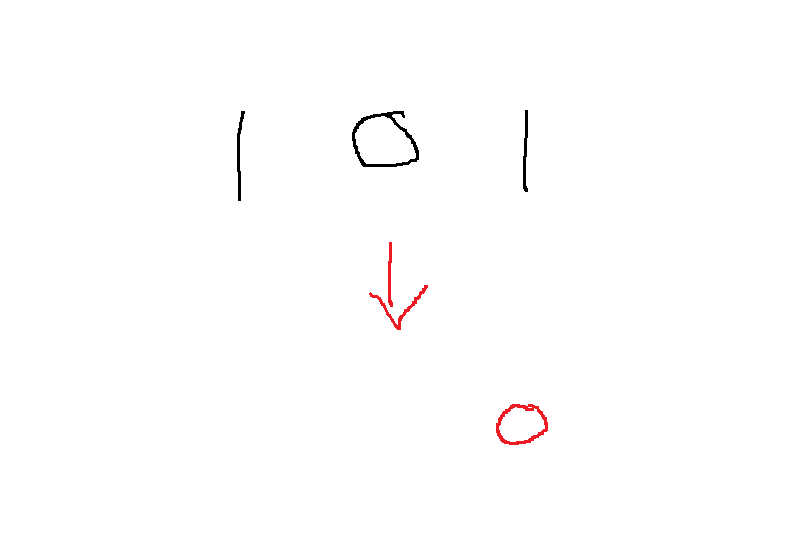
그 다음 첫번째 자리는 0인데, 0과 만날 수 있는 비트는 0과 1 모두 가능하다
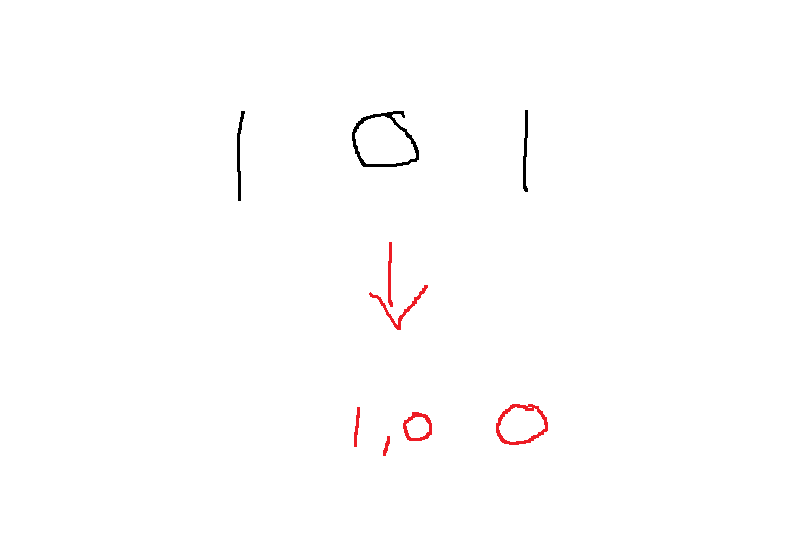
그 다음에 두번째 자리에는 1인데 1과 만날 수 있는 비트는 0이므로
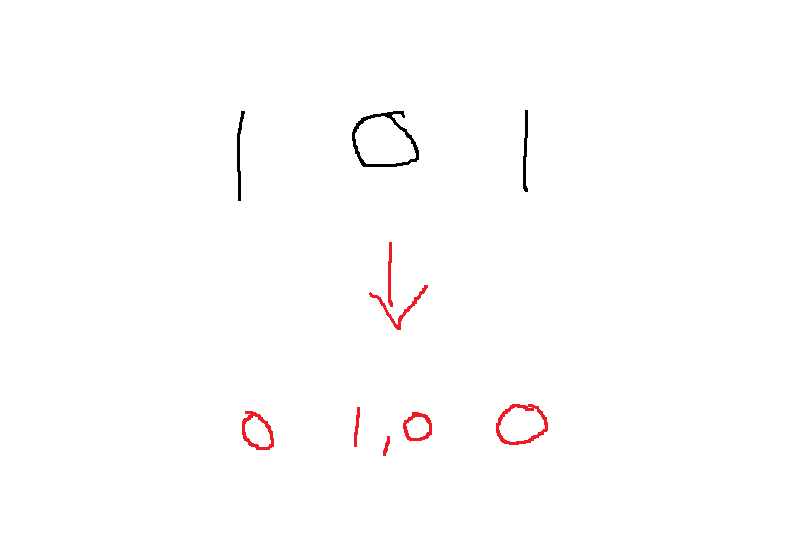
그 뒤로는 없는데 사실 101은 그 앞은 모두 0으로 채울 수 있다 000000....00000...000101 이렇게
그러니까 두번째 자리 이후로는 모두 0이다
따라서 두번째 자리 이후로는 그 다음 숫자는 1이나 0 모두 올 수 있다
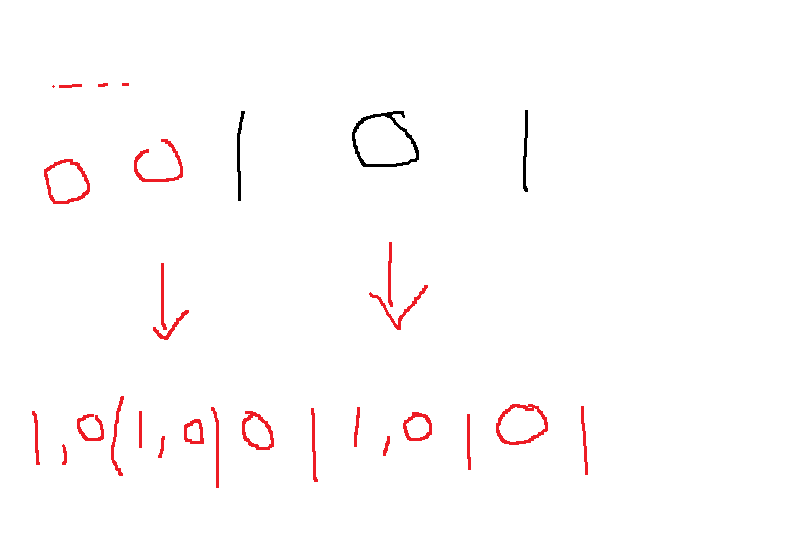
그러면 첫번째로 작은 수는 000으로 0인데 y는 자연수니까 이거는 불가능하고 1이 와야하니까 010
두번째로 작은 자연수는? 1000이다
세번째로 작은 자연수는? 1010
4번째로 작은 자연수는? 10000
...
특징이 1번째로 작은 자연수는 1은 2진수로 1이라서 010으로 1을 넣었고
2번째로 작은 자연수는 2는 2진수로 10이라서 1000으로 10을 넣었다
마찬가지로 3번째로 작은 자연수는 3이 2진수로 11이라서 11을 집어넣어서 1010이 된다
4번째로 작은 자연수 4는 2진수로 100이라서 10000이 된다
그래서 x를 먼저 2진수로 바꾸고 순회해서 bit가 1인 부분은 모두 0으로 바꾼다
bit가 0인 부분은 k를 집어넣을 수 있는 부분으로 표시해둔다
다음 k를 2진수로 바꾼 다음 x의 bit가 0이었던 부분에 k를 그대로 집어넣으면 된다
#x+y = x|y를 만족하는 k번째 작은 자연수 y를 찾는 문제
#x,y의 같은 위치의 비트가 서로 0,0이거나 0,1이거나 1,0이어야한다
x,k = map(int,input().split())
k = bin(k)[2:]
x = list(bin(x)[2:][::-1])
j = len(k)-1
#x를 2진수로 바꾸고 1인 부분은 모두 0으로 바꾼다
#0인 부분에는 k를 그대로 집어넣는다
for i in range(len(x)):
if x[i] == '0':
if j >= 0:
x[i] = k[j]
j -= 1
else:
x[i] = '0'
#k를 아직 다 집어넣지 못했다면 x의 뒷부분에 넣어야하므로...
while j >= 0:
x.append(k[j])
j -= 1
x = ''.join(x[::-1])
print(int(x,2))
'알고리즘 > 비트마스킹' 카테고리의 다른 글
| Kernighan’s Algorithm (0) | 2025.02.02 |
|---|---|
| 이진수의 마지막 n개의 비트가 모두 켜져있는지 확인하는 방법 (0) | 2024.05.03 |
| 비트마스크를 이용한 에라토스테네스의 체 배우기 (0) | 2023.05.04 |
| 정수 n을 2의 거듭제곱으로 나눈 나머지를 효율적으로 구하는 방법 (0) | 2023.05.03 |
| 비트마스킹 연습하기1(백준 25166,12833) (0) | 2022.10.30 |

