1. 문제
0과 1로 구성된 이진 비트열에서 1의 개수를 구한다면?
'1101'이면 1이 3개
2. 방법1
간단하게 비트열을 돌아서 1의 개수를 세기
시간복잡도는 비트열의 길이를 S라 하면 O(S)
s = '1101'
count = 0
for i in range(len(s)):
if s[i] == '1':
count += 1
print(count)
비트열이 주어지지 않고 단순히 정수로 주어질 수 있다
예를 들어 '1101' = 13인데 이진 비트열로 바꾸지 않고 구할 수 있나?
n의 마지막 비트와 1을 and연산하여 1이면 counting하고 n의 마지막 비트를 삭제해나간다
비트를 삭제하는 방법은 n >> 1
n의 비트를 오른쪽으로 1칸 이동시키고 최하위비트는 소멸된다
1101 >>> 0110
n = 13
count = 0
while n > 0:
count += n & 1
n >>= 1
print(count)
시간복잡도는 비트열의 길이가 S라하면 O(S)
정수 N에 대하여 O(logN)
3. Brian Kernighan’s Algorithm
십진수에서 1을 빼면, 가장 오른쪽에 있는 1인 비트부터 그 이후가 모두 반전된다
예를 들어 10 = '1010'인데 가장 오른쪽에 있는 1인 비트는 2번 위치
9 = '1001'인데 2번,3번 위치 비트가 원래 1,0이었다가 0,1로 바뀌었다
8 = '1000'인데 9에서 가장 오른쪽 1인 비트는 3번 위치인데, 이 비트가 0으로 바뀜
7 = '0111'인데 8에서 가장 오른쪽 1인 비트는 0번 위치인데 이후 비트가 모두 반전됨
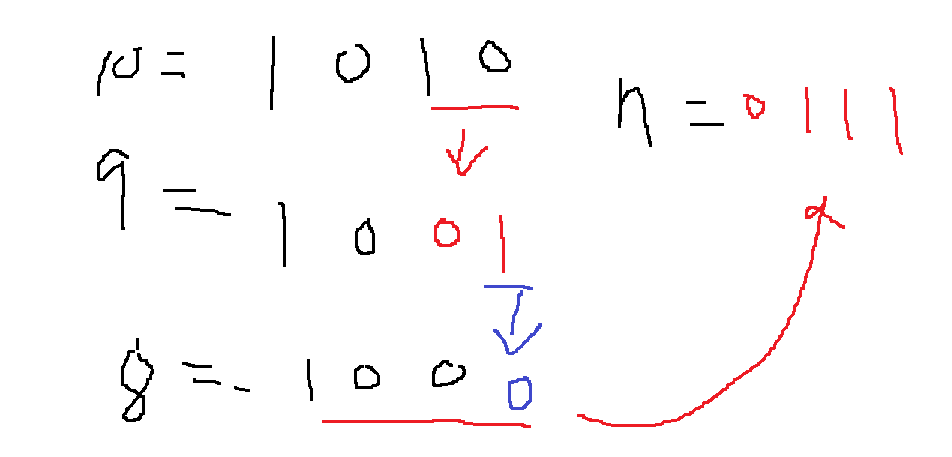
정수 n에서 1을 빼면 가장 오른쪽에 있는 1인 비트부터 그 이후가 모두 반전된다
그러므로 n과 n-1을 &연산을 한다면?
n의 가장 오른쪽에 있는 1인 비트를 기준으로 그 이후는 n-1과는 서로 다른 비트이고
그 이전은 n-1과는 서로 같은 비트이며 &연산은 서로 같으면 그대로 나오고, 서로 다르면 0으로 나오므로
n의 가장 오른쪽에 있는 1인 비트가 삭제된다는것
따라서 n & (n-1)을 반복적으로 연산하면 1인 비트가 모두 지워지므로, 이 반복 횟수가 1인 비트의 개수가 된다
즉 1인 비트의 개수만큼 반복하면 답을 찾을 수 있다는 뜻
n = 13
count = 0
while n > 0:
n &= (n-1)
count += 1
print(count)
이게 뭐가 필요하냐? 그럴 수 있는데
극단적으로 다음과 같이 실험해보면 10^7자리 이진비트열을 가지고 해보면 이 알고리즘은 바로 답이 나오는데

그냥 단순히 세는 알고리즘은 40분 걸리네

'알고리즘 > 비트마스킹' 카테고리의 다른 글
| 합과 bitwise or연산이 같게되는 조건 (0) | 2025.01.09 |
|---|---|
| 이진수의 마지막 n개의 비트가 모두 켜져있는지 확인하는 방법 (0) | 2024.05.03 |
| 비트마스크를 이용한 에라토스테네스의 체 배우기 (0) | 2023.05.04 |
| 정수 n을 2의 거듭제곱으로 나눈 나머지를 효율적으로 구하는 방법 (0) | 2023.05.03 |
| 비트마스킹 연습하기1(백준 25166,12833) (0) | 2022.10.30 |

