1. 신장트리(spanning tree)
n개의 정점으로 이루어진 "무방향 그래프"에서 n개의 정점과 n-1개의 간선으로 이루어진 트리
하나의 그래프가 있을때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프
이때, 모든 노드가 포함되어 서로 연결되면서 사이클이 존재하지 않는다는 조건은 트리의 성립 조건이다.
그래서 이러한 그래프를 신장 트리라고 부른다.

위와 같은 그래프에서 신장 트리는 여러개 찾을 수 있다.
예를 들어 아래와 같은 그래프는 하나의 신장 트리이다.

하지만 다음 그림과 같은 그래프들은 신장 트리가 아니다.
구체적으로 다음은 노드 1을 포함하고 있지 않다
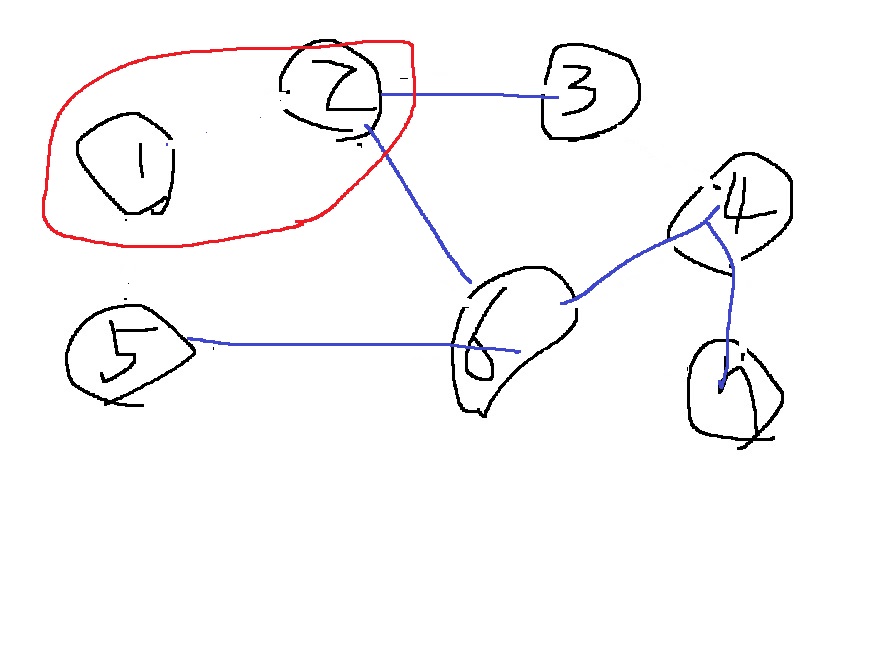
다음은 노드 4-6-7에서 사이클이 발생하므로 신장트리가 아니다.

2. 최소 신장 트리(Minimum spanning tree)
무방향 가중치 그래프에서 신장 트리를 구성하는 간선들의 가중치 합이 최소인 신장 트리
우리는 다양한 문제 상황에서 가능한 한 최소한의 비용으로 신장 트리를 찾아야 할 때가 있다.
예를 들어 3개의 도시 A,B,C가 있고 두 도시 사이에 도로를 놓아 전체 도시가 서로 연결될 수 있도록 도로를 설치하고 싶다.
여기서 최소한의 비용으로 전체 도시가 서로 연결될 수 있도록 도로를 놓고자 한다면, 어떻게 할 수 있을까?
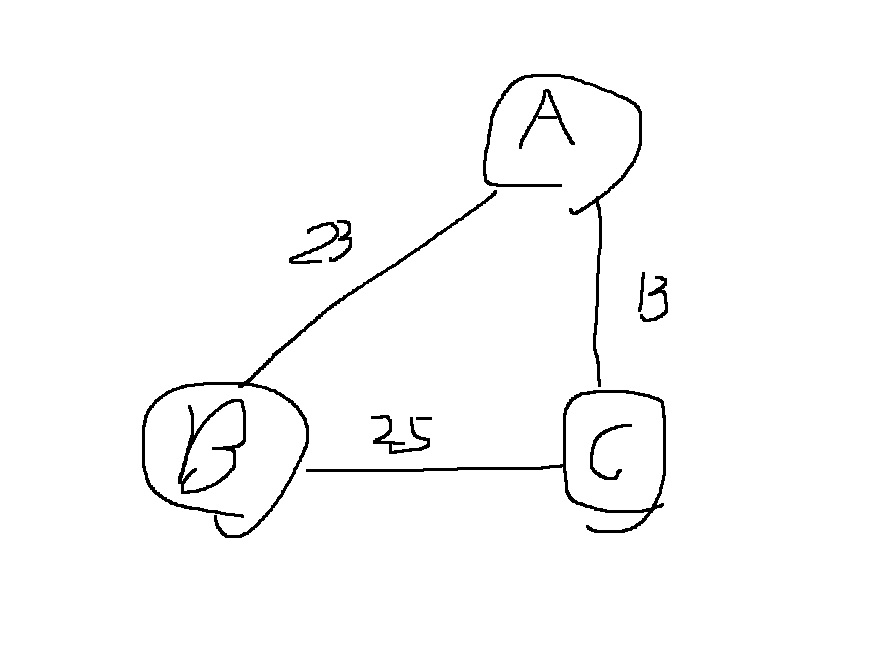
위와 같이 A-B를 연결하는 비용이 23, B-C를 연결하는 비용이 25, A-C를 연결하는 비용이 13이라면..
여기서 노드 A,B,C가 모두 연결되는 최소한의 비용은 다음과 같은 36이다.

3. 크루스칼 알고리즘(Kruskal algorithm)
대표적인 최소 신장 트리를 찾는 알고리즘
가장 적은 비용으로 모든 노드를 연결할 수 있는데, 그리디 알고리즘으로 분류된다.
간선을 하나씩 선택하여 MST를 찾는 알고리즘이다.
먼저 모든 간선에 대하여 정렬을 수행한 뒤에 가장 거리가 짧은 간선부터 집합에 포함시키면 된다.
이때 사이클을 발생시킬 수 있는 간선의 경우에는 집합에 포함시키지 않는다.
3-1) 알고리즘
1) 모든 간선 데이터를 비용(가중치)에 따라 오름차순으로 정렬
2) 가중치(비용)가 적은 간선부터 하나씩 선택하는데.. 사이클이 발생하는지 확인한다
2-1) 사이클이 발생하지 않으면 최소 신장 트리에 포함
2-2) 사이클이 발생하면 최소 신장 트리에 포함시키지 않는다
3) 모든 간선에 대하여 2)를 반복하여, n-1개의 간선을 선택하면 종료
4. 예시를 통해 이해하는 크루스칼 알고리즘
다음 그래프에서 크루스칼 알고리즘에 따라 최소 신장 트리를 구해보자.
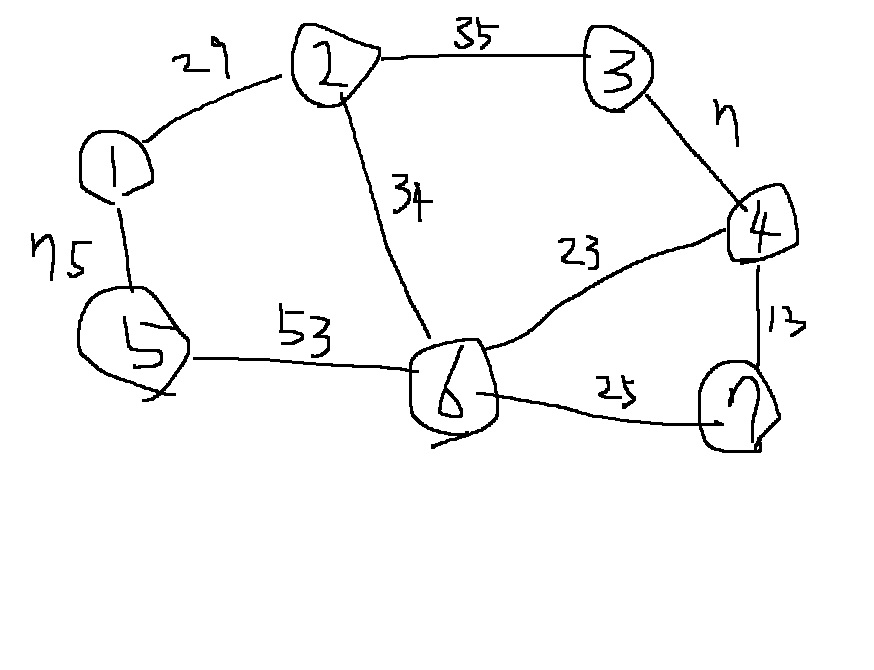
최소 신장 트리는 다음 그래프와 같이 하늘색으로 칠한 간선들을 포함시키면 만들 수 있다.
최소 신장 트리는 일종의 트리 자료구조이므로 최종적으로 신장 트리에 포함되는 간선의 개수는 반드시 "노드의 개수-1"이다.

핵심 원리는 거리가 가장 짧은 간선부터 차례대로 집합에 추가시키는 것이다.
단 사이클이 발생하는 간선은 제외하고 연결한다.
이렇게 하면 항상 최적의 해를 보장할 수 있다.
어떻게 하면 찾을 수 있을까?? 구체적으로 따라가보자.
4-1) 초기 단계에서는 그래프의 모든 간선 정보만 따로 빼내어 정렬을 수행한다. 현재 전체 그래프에서 존재하는 간선은 9개이다. 여기서 간선의 가중치를 기준으로 오름차순으로 정렬한다

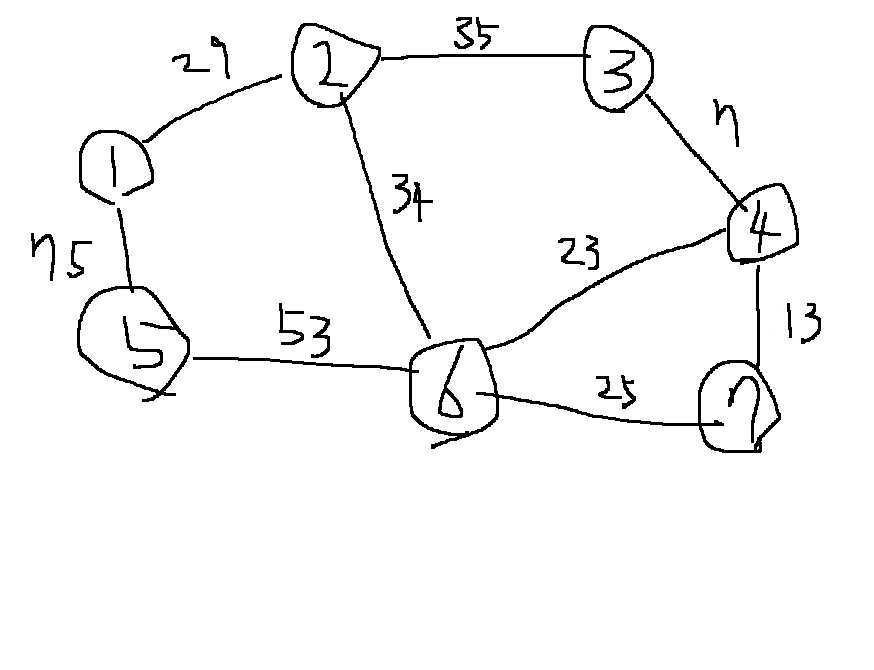
4-2) 첫번째 단계에 가장 짧은 간선인 (3,4)를 선택한다. 따라서 (3,4)가 선택되고 이것을 집합에 포함하면 된다.
다시 말해 노드 3과 노드 4에 대하여 union 함수를 수행한다. 그러면 노드 3과 노드 4를 동일한 집합으로 만든다.

4-3) 다음 단계에는 비용이 가장 작은 간선인 (4,7)을 선택한다. 현재 노드 4와 노드 7은 같은 집합에 속해있지 않으므로 노드 4와 7에 대한 union 함수를 수행한다.
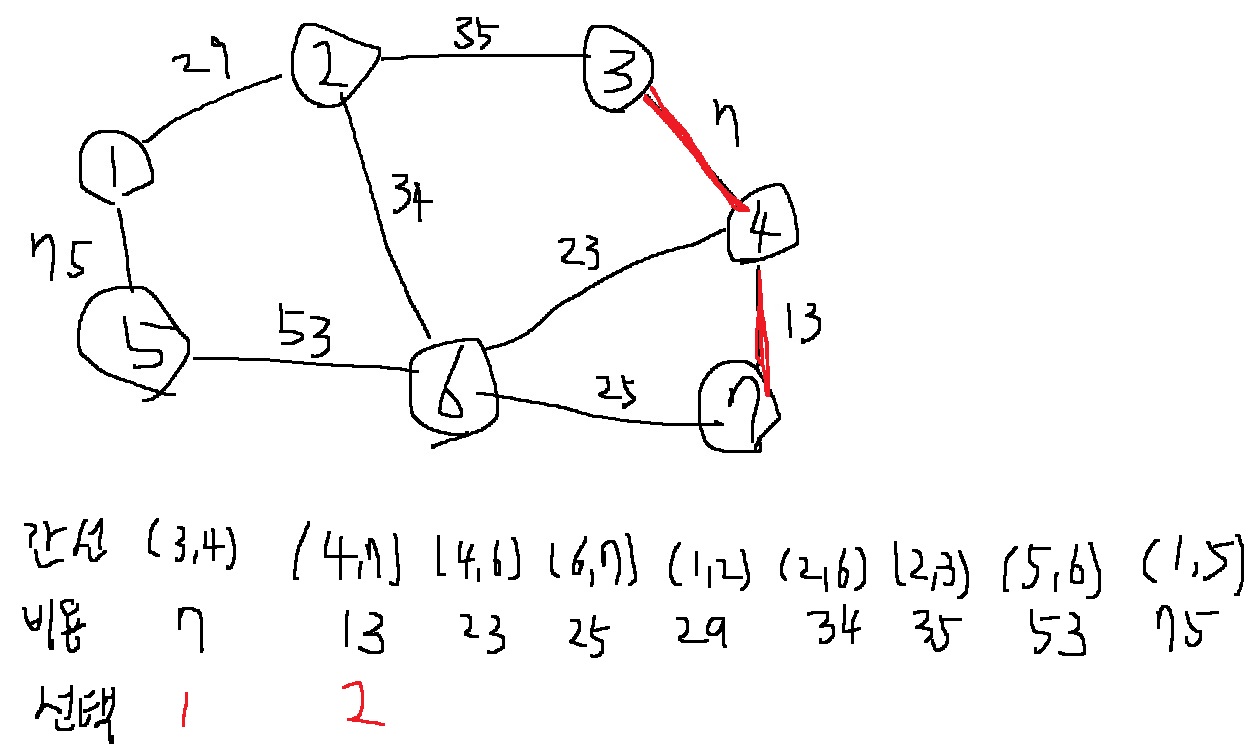
4-3) 그 다음으로 비용이 가장 작은 간선인 (4,6)을 선택한다. 현재 노드 4와 노드 6은 같은 집합에 속해 있지 않으므로, 노드 4와 노드 6에 대해 union 함수를 수행한다.

4-4) 그 다음으로는 비용이 가장 작은 간선인 (6,7)을 선택한다. 선택된 노드 6과 노드 7의 루트 노드를 확인하자.
그런데 6과 7은 이미 동일한 집합에 포함되어 있으므로, 신장 트리에 포함하지 않아야한다.
즉 (6,7)을 포함하면 사이클이 발생하므로 최소신장트리에 포함하지 않는다.
그러므로 union 함수를 호출하지 않는다.
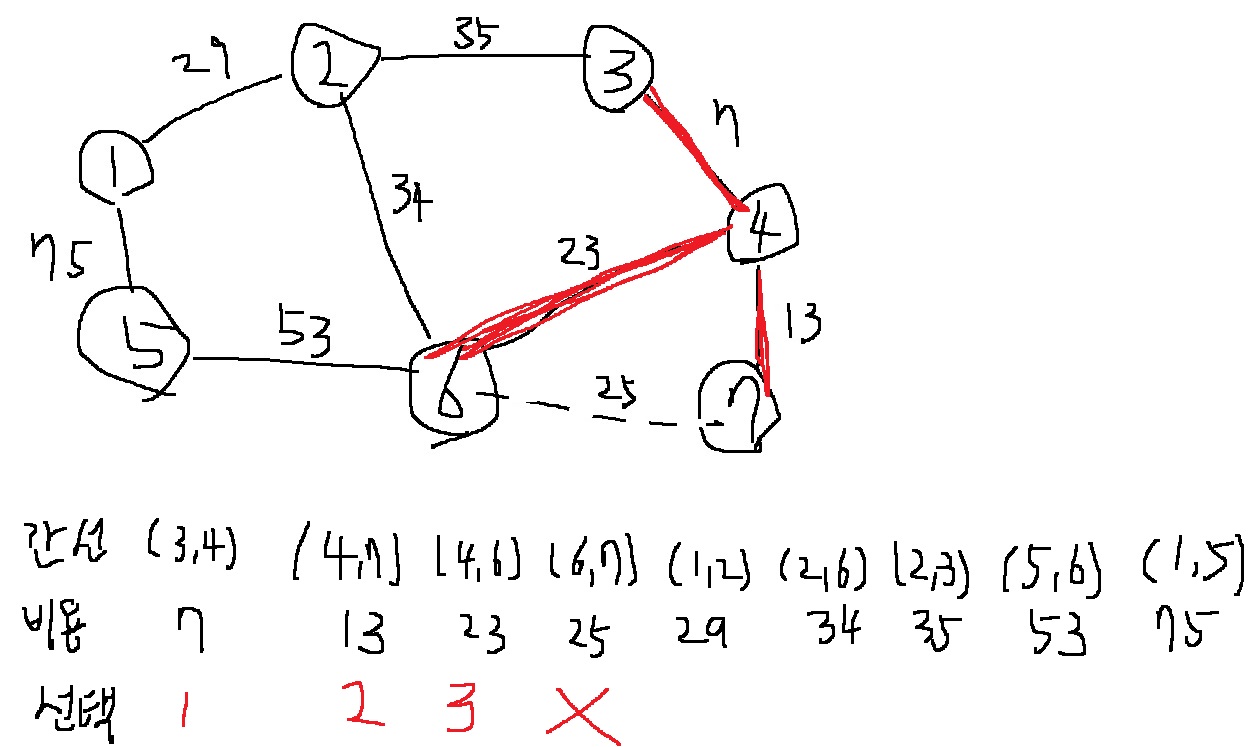
4-5) 그 다음으로 비용이 가장 작은 간선인 (1,2)를 선택한다. 노드 1과 노드 2는 같은 집합에 속해 있지 않으므로 노드 1과 노드 2에 대해 union 함수를 호출한다.

4-6) 그 다음으로 비용이 가장 작은 간선인 (2,6)을 선택한다. 현재 노드 2와 6은 같은 집합에 속해있지 않으므로 역시 union 함수를 호출한다.
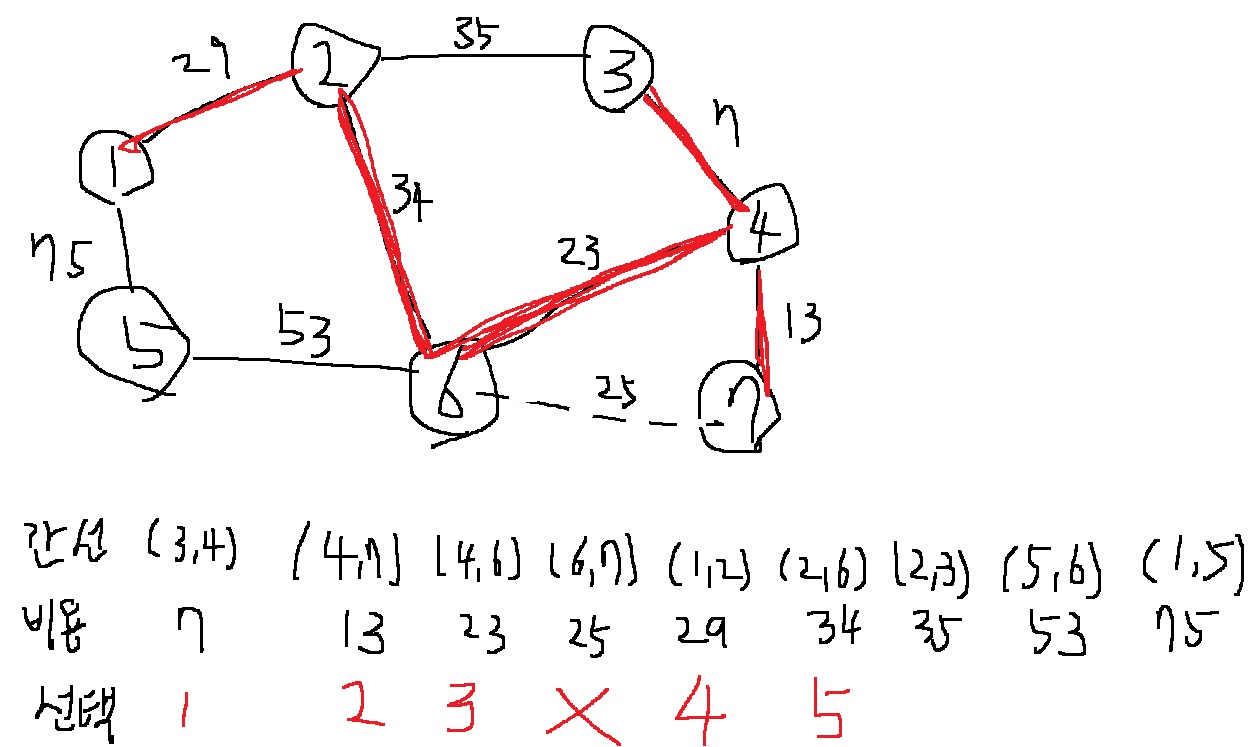
4-7) 그 다음으로 비용이 가장 작은 간선인 (2,3)을 선택한다. 그런데 2와 3은 같은 집합에 속해있으므로, (2,3)을 포함하면 사이클이 발생한다. 그러므로 (2,3)은 포함하지 않는다.
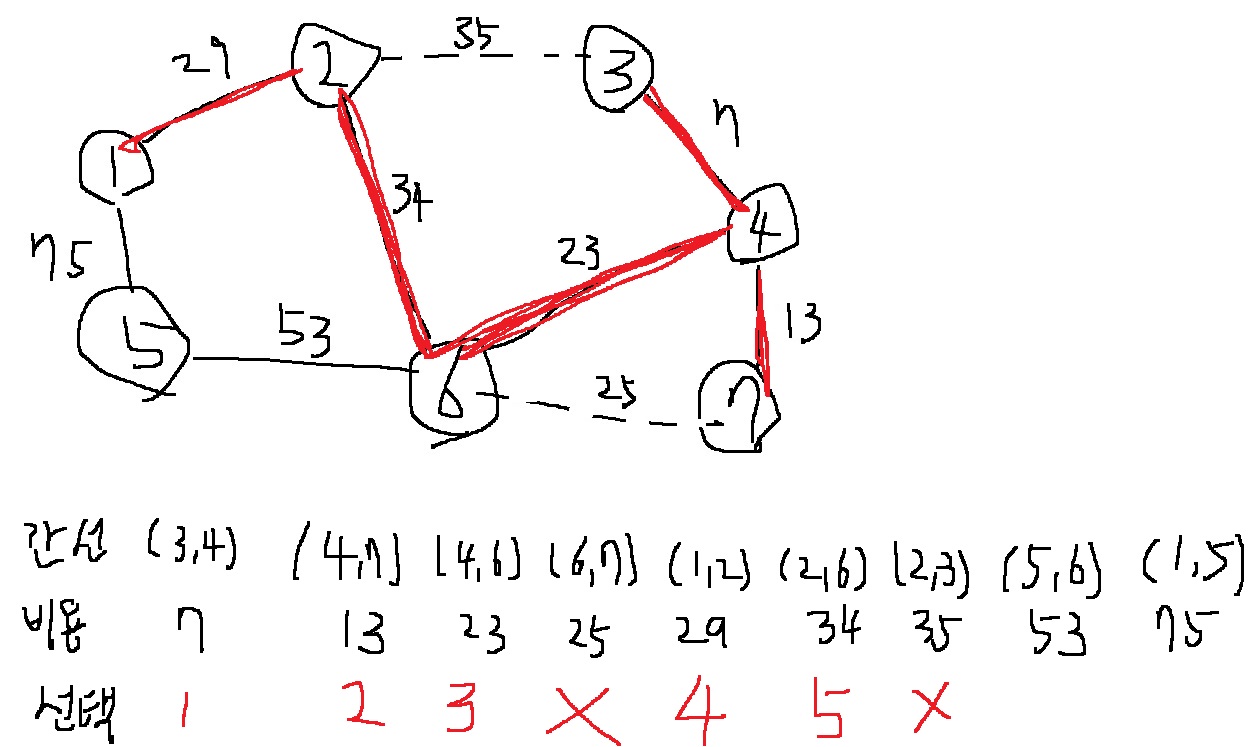
4-8) 그 다음으로 비용이 가장 작은 간선인 (5,6)을 선택한다. 노드 5와 6은 같은 집합에 속해 있지 않으므로 노드 5와 6에 대하여 union 함수를 호출한다
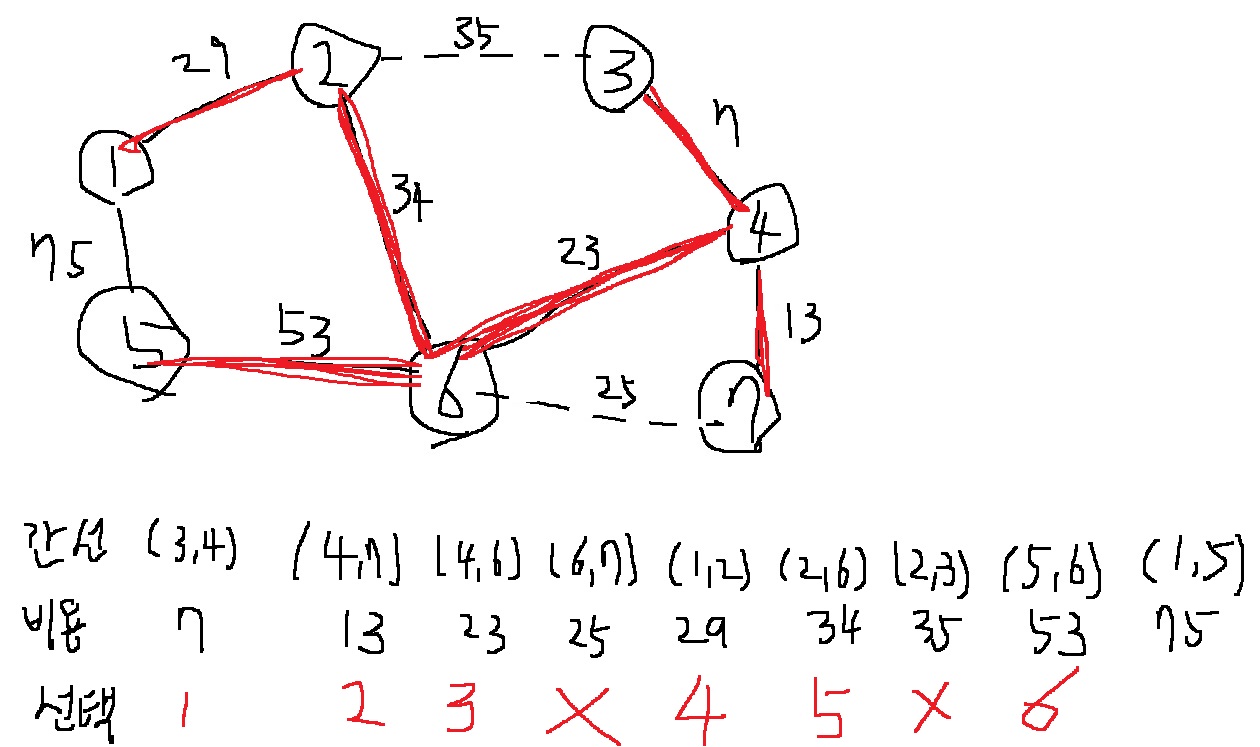
4-9) 다음으로 비용이 가장 작은 간선인 (1,5)를 선택한다. 선택된 노드 1,5는 같은 집합에 속해있으므로 union 함수를 호출하지 않는다.
포함하면 사이클이 발생하게 되므로 포함시키지 않는다.

결과적으로 위와 같은 최소 신장 트리를 얻는다.
최소 신장 트리에 포함되어 있는 간선의 가중치를 모두 더하면 최종 최소 비용 159를 얻는다.
5. 크루스칼 알고리즘 구현 예시
union, find함수를 만들고
parent, rank 배열을 초기화한다.
여기서 parent를 최초 자기 자신을 부모로 설정하는 것을 자주 깜빡하는데 주의한다
다음 그래프의 모든 간선을 따로 받아 edges로 만든다
여기서 정렬하기 편하게 (cost,a,b) 순서로.. cost를 먼저 나오게 만들자
다음 비용으로 오름차순 정렬된 edges의 모든 간선을 하나씩 확인하여 사이클이 발생하는지 확인하자
사이클 발생여부는 find_parent 함수 값이 서로 같다면 발생한 것이다.
즉 find_parent함수 값이 서로 다르다면 사이클이 발생하지 않아서, union 함수를 수행하고
해당하는 비용을 누적시킨다.
선택한 간선의 수에도 1을 더해주고, 선택한 간선의 수가 정점의 수-1이 되면 반복문을 멈춰준다.
## 특정 원소가 속한 집합을 찾는 함수
##path compression 적용
def find_parent(parent,x):
##루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if x != parent[x]:
parent[x] = find_parent(parent,parent[x])
return parent[x]
"""
def find_parent(parent,x):
while parent[x] != parent[parent[x]]:
parent[x] = parent[parent[x]]
return parent[x]
"""
##두 원소가 속한 집합을 합치는 함수
##union by rank 적용
def union_parent(parent,a,b):
##a,b의 대표자를 찾고
a = find_parent(parent,a)
b = find_parent(parent,b)
##rank가 낮은 부모를 높은 노드 번호로
if rank[a] > rank[b]:
parent[b] = a
else:
parent[a] = b
if rank[a] == rank[b]: ##rank가 동일하면
rank[b] += 1 ##한쪽 rank를 1 증가
"""
def union_parent(parent,a,b):
a = find_parent(parent,a)
b = find_parent(parent,b)
if parent[a] > parent[b]:
parent[parent[b]] = parent[a]
else:
parent[parent[a]] = parent[b]
"""
##노드와 간선의 개수 입력받는다
v,e = map(int,input().split())
##부모 테이블 초기화
parent = [0]*(v+1)
rank = [0]*(v+1) ##union by rank를 위한 rank배열
##최초 부모를 자기 자신으로 초기화함
#parent = [i for i in range(v+1)]
for i in range(1,v+1):
parent[i] = i
##모든 간선을 담을 리스트와 최종 비용
edges = []
result = 0
##모든 간선에 대한 정보 받기
for _ in range(e):
a,b,cost = map(int,input().split())
edges.append((cost,a,b)) ##cost가 작은 순으로 오름차순 정렬을 위해 cost를 앞에 두기
##간선을 가중치 비용 순서대로 오름차순 정렬
edges.sort()
##크루스칼 알고리즘
cnt = 0 ##최소신장트리를 위해 선택한 간선의 개수
for edge in edges:
cost,a,b = edge ##비용이 적은 간선을 하나씩 확인하여
##노드 a와 노드 b가 동일한 집합에 속하지 않는다면..
##즉 사이클이 발생하지 않는다면..
##즉 find_parent()값이 서로 다르다면..
if find_parent(parent,a) != find_parent(parent,b): ##동일한 집합에 속하지 않는 경우
union_parent(parent,a,b) ##union 수행
result += cost ##union을 수행한 간선의 가중치를 더해준다
cnt += 1 ##해당 간선 선택
if cnt == v-1: ##정점의 수 -1만큼의 간선을 선택하면
break ##더 이상 선택할 필요가 없다
print(result) ##최소신장트리의 최소비용
6. 시간복잡도
간선의 개수가 e개 일때 시간이 가장 오래 걸리는 부분은 간선을 정렬하는 작업으로 가장 빠르게 정렬하면 O(eloge)가 된다.
내부에서 사용되는 union find 알고리즘의 시간 복잡도는 정렬 알고리즘보다 작아 무시한다.
7. 연습문제
1197번: 최소 스패닝 트리 (acmicpc.net)
1197번: 최소 스패닝 트리
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이
www.acmicpc.net
풀이 코드가 위에 있는거랑 완전히 동일해서 굳이.. 써야하나?
'알고리즘 > 최소 스패닝 트리' 카테고리의 다른 글
| 최소 스패닝 트리를 이용해서 그래프를 두 집합으로 분리하기(크루스칼 알고리즘 미세팁) (0) | 2023.07.27 |
|---|---|
| 최대 비용을 가지는 신장 트리를 만드는 방법? (0) | 2023.04.20 |
| 최소 신장 트리를 구하는 프림 알고리즘, 크루스칼 알고리즘 재활하기1 (0) | 2023.04.18 |
| 최소 신장 트리를 찾는 두번째 알고리즘 - 프림 알고리즘 파헤치기 - (0) | 2022.10.03 |

