1. 힙(heap)
프로그램 실행중에 내가 사용할 수 있는 메모리 양이 변할 수 있는 경우, 그 때 사용하는 메모리 공간을 힙이라고도 하는데..
여기서는 자료구조를 말한다.
기본적으로 "완전 이진 트리"를 이용한 자료구조이다.
특히 "완전 이진 트리"에 있는 노드 중에서 키값이 가장 큰 노드나 가장 작은 노드를 찾기 위해 특별히 만든 자료구조
완전 이진 트리니까, n개의 노드가 주어진다면 길이 n+1의 단순 배열로 저장할 수 있다
처음에 만들때, 키값이 가장 큰 노드를 찾는 자료구조를 만들 것이냐, 키값이 가장 작은 노드를 찾는 자료구조를 만들 것이냐,를 정하고 들어간다.
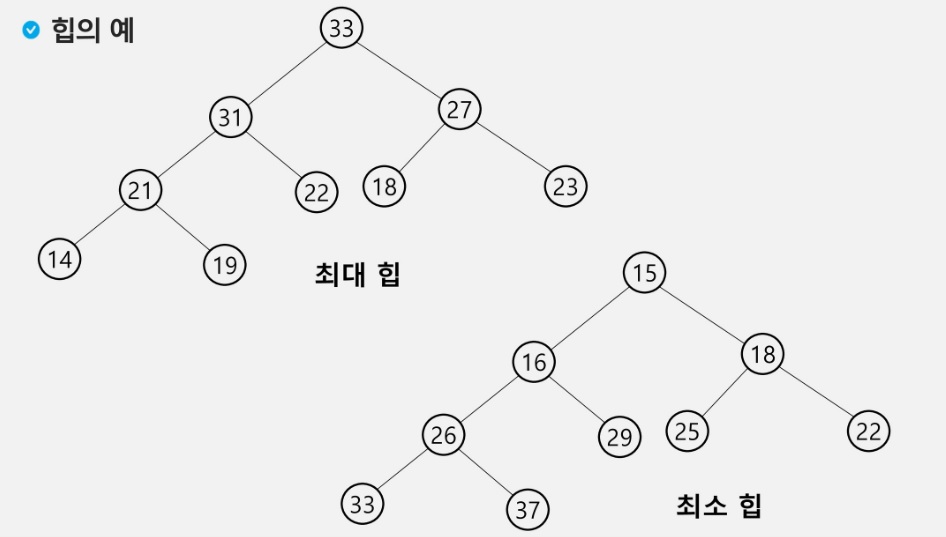
2. 최대힙(max heap)과 최소힙(min heap)
2-1) 최대힙(max heap)
키값이 가장 큰 노드를 찾기 위한 완전 이진 트리
모든 노드에 대해, 항상 "부모 노드의 키 값 > 자식 노드의 키 값"
그러므로 루트 노드에는 항상 모든 노드중에서 키 값이 가장 큰 노드가 된다
2-2) 최소힙(min heap)
키 값이 가장 작은 노드를 찾기 위한 완전 이진 트리
모든 노드에 대해, 항상 "부모 노드의 키 값 < 자식 노드의 키 값"
그러므로 루트 노드에는 항상 모든 노드중에서 키 값이 가장 작은 노드가 된다.
3. 예시로 이해하는 최대힙의 삽입연산 알고리즘
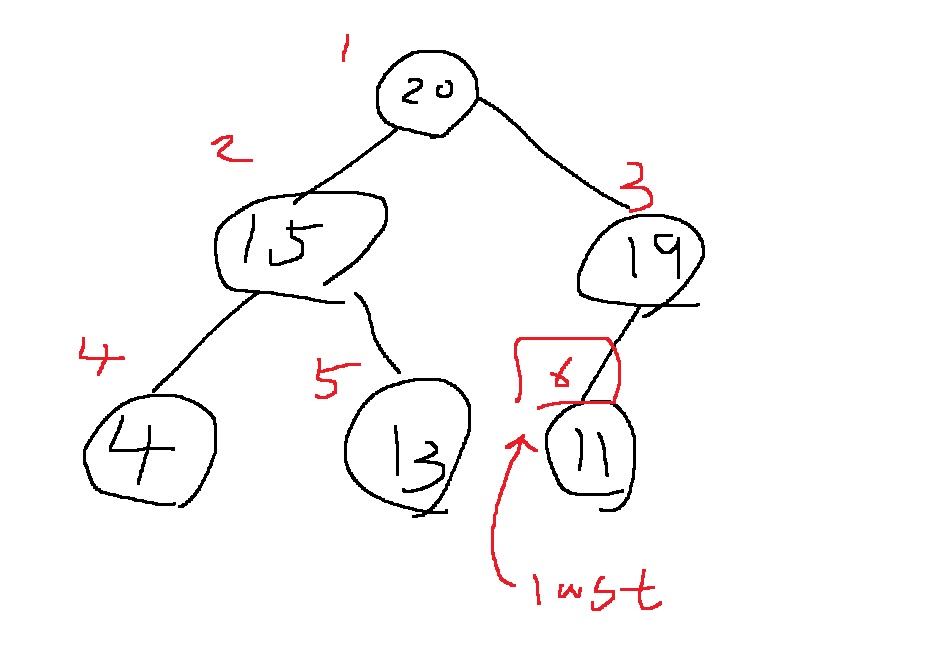
다음과 같은 힙에서 17을 삽입한다고 생각해보자.
삽입하기 전에 마지막 인덱스에 대한 정보를 파악해야한다
현재 최대 n개짜리의 힙을 만든다고 생각할 때, 위 그림은 다음과 같은 단순 배열로 저장되어 있을 것임

기본적으로 완전이진트리를 항상 유지해야하고, 현재 마지막 정점의 번호는 last = 6
append로 넣는거 가능하지만, 느려져서 크기를 정하고 구현한다고는 하는데..
아무튼 일단 크기를 정하고 구현을 해보자고
완전이진트리를 유지해야하므로 어떤 값을 넣고자 할때, 마지막 정점의 번호+1을 해준다
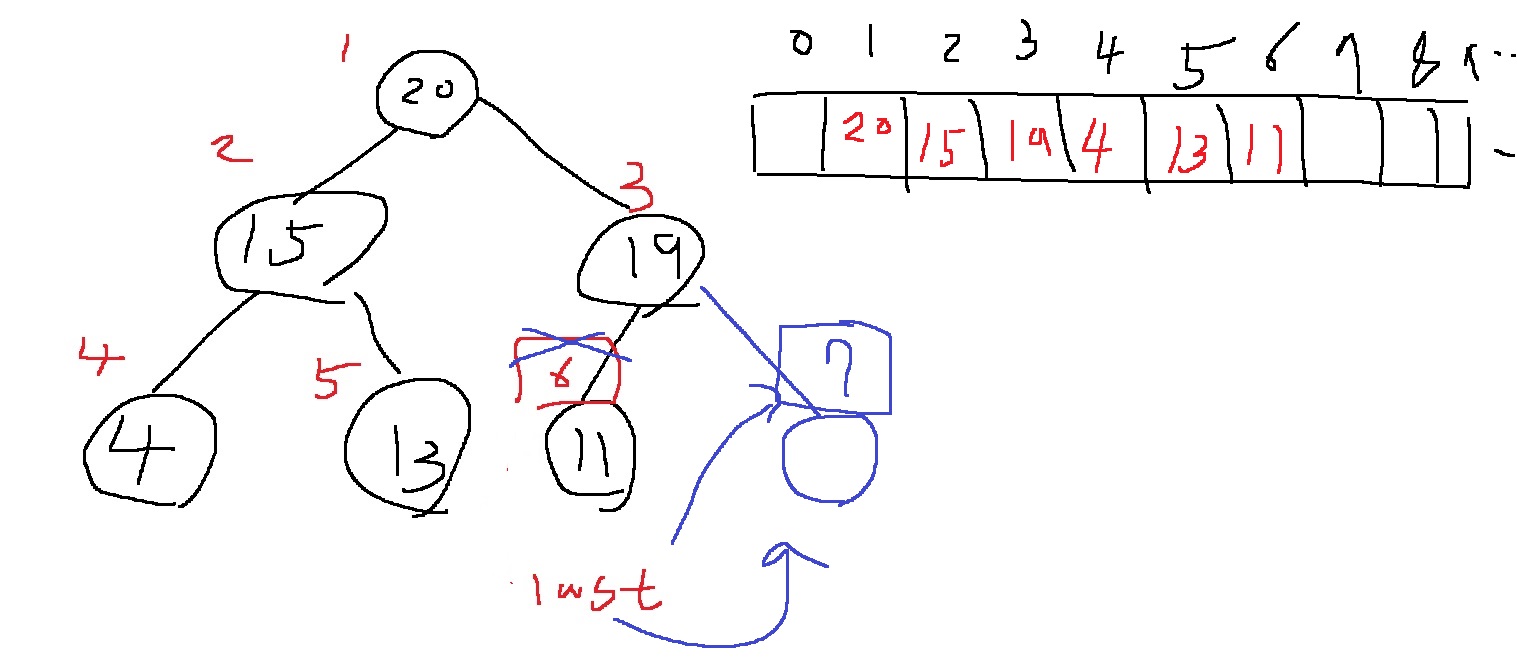
그리고 마지막 자리에 원하는 데이터를 삽입한다

다음으로, 최대힙(max heap) 조건을 만족시키게 만들어야한다.
"부모 노드의 키 값이 항상 자식 노드의 키 값보다 크다"
현재 넣어준 자리(7번)를 자식으로 하고 부모의 자리를 구한다. 완전이진트리이므로 7//2 = 3이니까 19와 비교하면..
부모 노드 19가 더 크니까 끝
---------------------------------------------------------------------------
이번엔 23을 삽입하는 상황을 생각해보자.
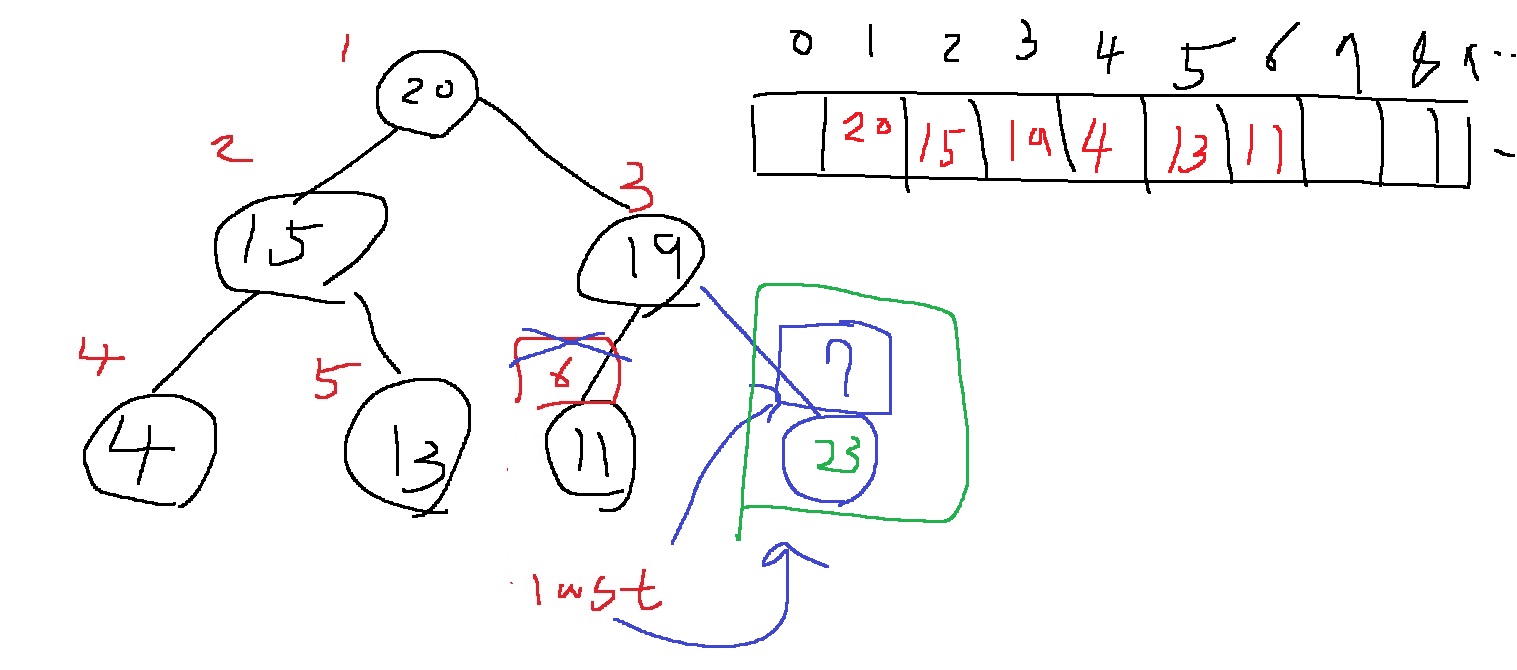
이번엔 현재 넣은 마지막 자리 23이 부모인 19보다 더 크므로, 최대힙의 조건 "부모 노드의 키 값이 자식 노드의 키 값보다 항상 크다"을 만족하지 않는다
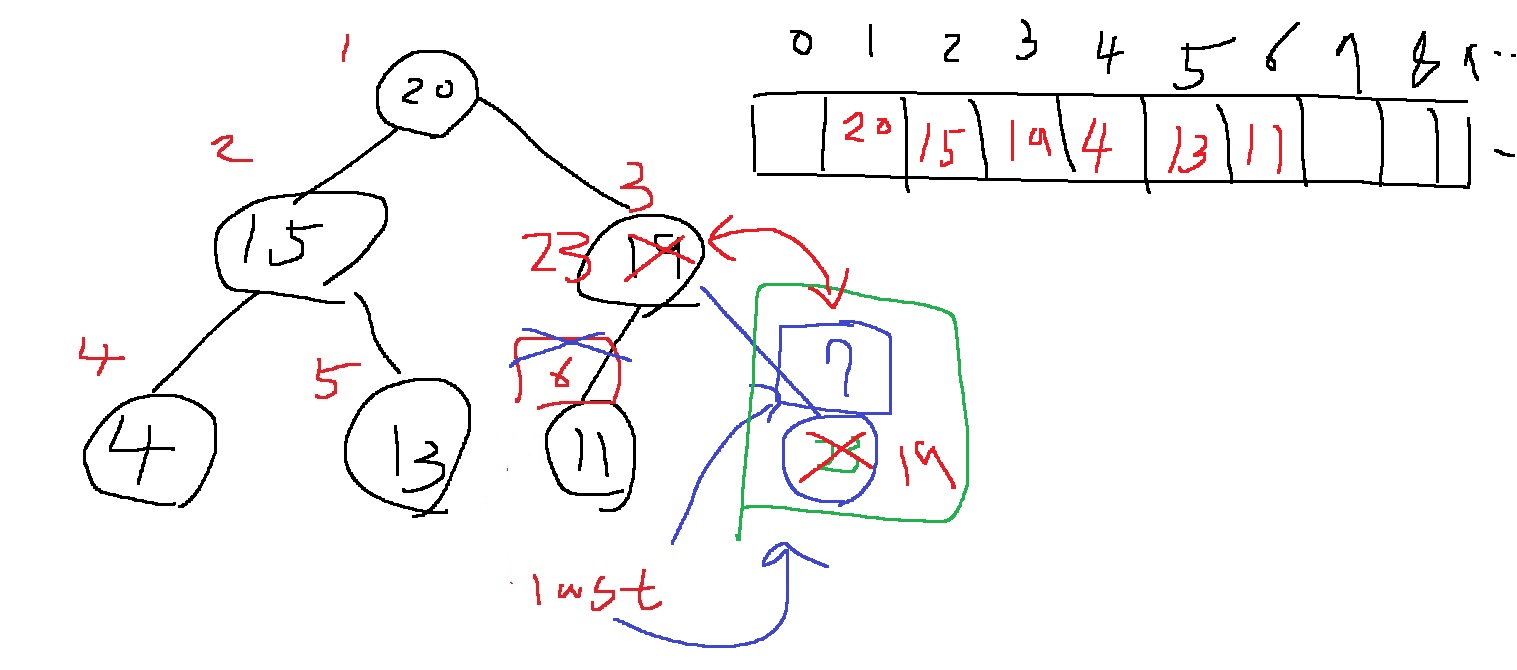
그러면 부모 노드의 키 값과 자식 노드의 키 값의 자리를 바꿔주면 된다.
그런데 바꾸고 끝이냐? 그렇진 않다
모든 노드에 대하여, "부모 노드의 키 값이 자식 노드의 키 값보다 크다"를 만족할때까지 계속해서 자리 교환을 수행함
현재 바뀐 23의 자리 3번을 자식으로 하여, 이것의 부모인 3//2 = 1번의 키 값과 비교한다
여전히 자식 노드의 값이 더 크다면 또 자리를 바꿔준다
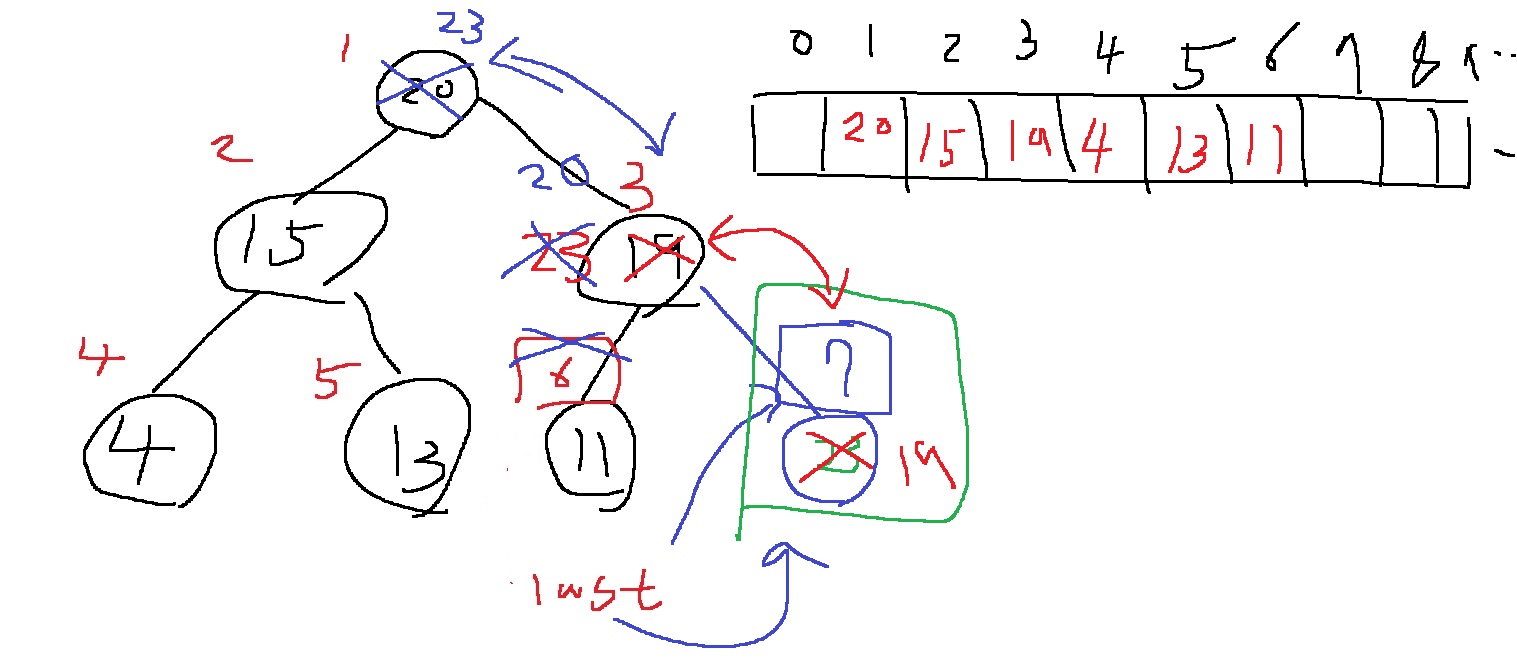
그러면 이제 1번자리로 올라온 23번도 역시 부모와 크기를 비교한다.
하지만 1번의 부모는 존재하지 않는다 끝
최종적으로 요약하자면 다음과 같다.
1) 마지막 정점 번호 + 1을 하여 그곳에 원하는 데이터를 삽입한다
2) 삽입한 자리의 번호를 자식으로 하여 부모를 찾고, 부모의 키 값과 자식의 키값을 비교한다
3) 최대힙이라면, 부모 노드의 키 값이 항상 더 커야하므로 그러한 조건을 만족할때까지 2)를 반복한다.
4) 조건을 모두 만족하여 자리를 바꿀 수 없거나, 더 이상 부모가 존재하지 않는다면 종료
-------------------------------------------------------------------------------------------------------
그러면 최소힙은 어떻게 함??
똑같이 하는데
3) 최대힙이라면, 부모 노드의 키 값이 항상 더 커야하므로 그러한 조건을 만족할때까지 2)를 반복한다.에서
"부모 노드의 키 값이 항상 더 작아야하므로, "로 바꿔주면 되겠지
하지만 최대힙이든 최소힙이든 완전이진트리를 항상 유지한다는 것은 변함 없다
4. 최대힙 삽입연산 구현 예시
위의 알고리즘 그대로 구현하면 된다
1)삽입할때마다 마지막 정점 + 1
2) 삽입한 자리의 번호를 자식으로, 그것의 부모를 구하고 둘을 비교해서 부모가 작으면 자리 교환
3) 더 이상 부모가 없거나, 부모 > 자식을 만족할때까지 2)를 반복
#최대크기는 10개짜리로
#최대힙 예시
#2,5,7,3,4,6,...
def enq(n):
global last
last += 1 ##마지막 정점을 추가시키는 작업
#빈 틀만 만들어진 상태
heap[last] = n #마지막 정점에 key값을 추가함
#부모 노드가 없거나,
#부모 노드의 크기 > 자식 노드의 크기일때까지
#반복적으로 자리를 교환함
#부모노드 크기 < 자식노드 크기이면 자리를 바꿔줌
##더 이상 부모가 없거나, 부모 > 자식 조건을 만족할때까지
c = last #삽입된 자식
p = c//2 #완전이진트리이므로, 부모 노드는 c//2
while p and heap[p] < heap[c]: #부모가 있고, 부모노드<자식노드이면 반복문을 계속 수행
heap[p],heap[c] = heap[c],heap[p] ##교환
#노드 값을 바꿨으면
#실제 노드 번호도 바꿔주고
c = p #이전 부모를 새로운 자식으로 하고
p = c//2 #그 자식의 부모를 구하는
heap = [0] * 10
last = 0
enq(2)
enq(5)
enq(7)
enq(3)
enq(4)
enq(6)
print(heap)
"""
[0, 7, 4, 6, 2, 3, 5, 0, 0, 0]
"""
5. 예시로 이해하는 최대힙의 삭제연산
힙에서는 루트 노드만 삭제할 수 있다
1번 원소가 루트 노드
배열 딱 불러서 아무데나 접근할 수는 있지만, 아무곳이나 삭제하면 까다로워지거든
최대힙이면 모든 원소중 최댓값을 얻고, 최소힙이면 모든 원소중 최솟값을 얻게된다
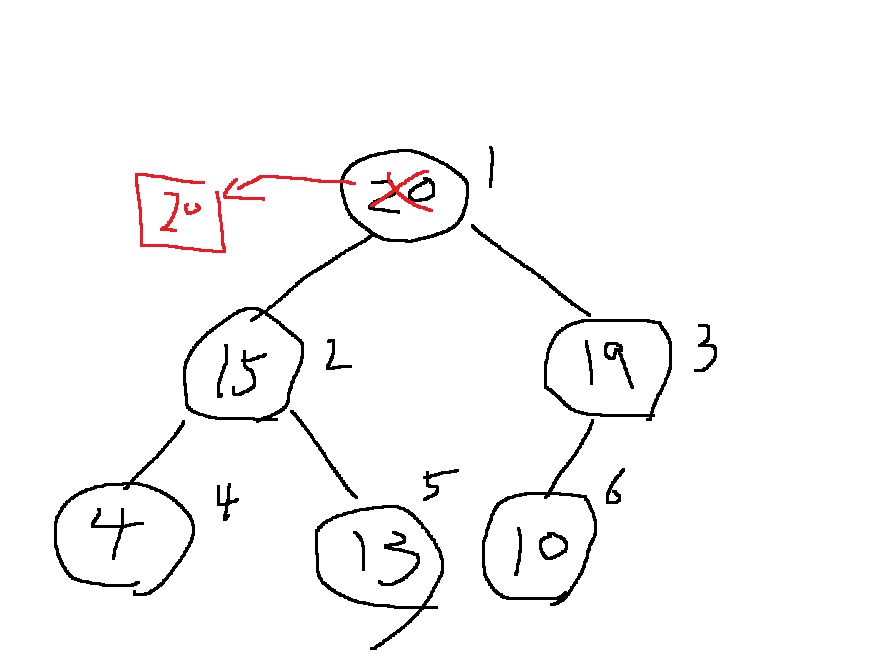
루트노드의 20을 삭제하여 어딘가에 저장해서 사용할것
그러면 이제 루트 자리가 비어있는데 일단 "완전이진트리"를 유지해야하므로 마지막 정점 6번에서 1을 빼서 완전이진트리를 유지시킨다
그런데 마지막 노드의 값은 당연히 존재해야하므로, 일단 루트로 옮긴다

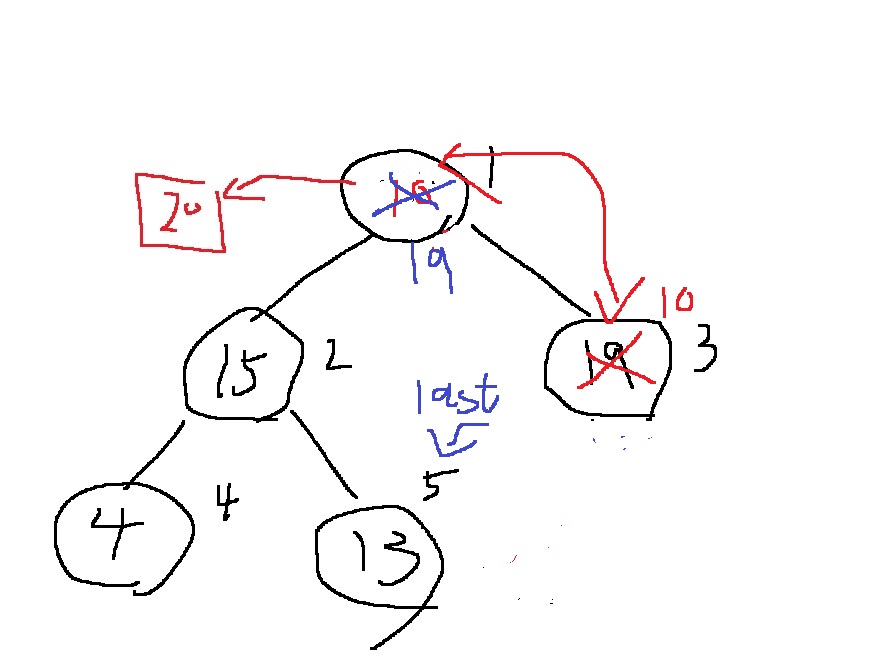
다음 최대힙 조건 "부모 노드 > 자식 노드"를 모든 노드에 대해 만족해야한다.
변화된 곳은 루트 노드 1번이므로, 1번을 부모로 하고 자식들의 크기를 비교한다
완전이진트리이므로, i번의 자식은 2i번이거나 2i+1번
당연히 자식이 둘이 존재한다면, 둘중 더 큰 값을 가지는 자식과 크기를 비교함
자식이 하나만 존재한다면 그 자식과 크기를 비교함
위 과정을 계속 반복함
언제까지?? 당연히 "자식이 존재하고, 부모 < 자식이면 자리를 교환"
그런데 삽입과는 다르게 두개의 자식이 존재하면, 어떤 자식과 교환을 해야할지 고려하는 작업이 필요
6. 최대힙의 삭제연산 구현 예시
위의 알고리즘을 그대로 구현하면 된다
1) 루트노드 값을 가져오고
2) 마지막 노드의 값을 루트 노드에 넣은 뒤, 마지막 노드 번호 - 1
3) 부모를 1번으로 하고 자식과 크기를 비교함, 자식이 둘 존재하면 더 큰 자식과 비교하고 하나만 존재하면 하나의 자식과 비교
4) 더 이상 자식이 없거나, 부모 > 자식이 된다면 교환 중단
##최대힙 삭제연산 에시
def deq():
global last
##루트 값을 백업해둔다
tmp = heap[1] ##완전이진트리이므로 1번이 루트
##마지막 노드의 키값을 루트에 복사
heap[1] = heap[last]
##마지막 노드 삭제
last -= 1
##루트에 옮긴 값을 자식과 비교하여 교환하기
p = 1 ##현재 부모는 1번
c = p*2 ##일단 왼쪽 자식 먼저
while c <= last: ##자식이 하나라도 존재한다면..
##혹시 오른쪽 자식도 있고, 오른쪽 자식이 더 크면..?
if c + 1 <= last and heap[c] < heap[c+1]: ##오른쪽 자식도 존재하고, 그것이 왼쪽 자식보다도 더 크다면
c += 1 ##실제 비교 대상을 오른쪽 자식으로
##부모보다 자식이 더 크다면 최대힙 규칙에 어긋나서 교환을 수행
if heap[p] < heap[c]:
heap[p],heap[c] = heap[c],heap[p]
##앞으로도 자식과 부모를 교환해야할 수도 있으므로
##새롭게 초기화작업
p = c #현재 바뀐 자식을 새로운 부모로
c = p*2 ##바뀐 부모에 대해 새로운 왼쪽 자식
else: ##부모가 더 크다면, 교환작업을 중단
break
return tmp ##삭제한 루트값 반환
7. 힙정렬(heap sort)
실제로 잘 동작하는지를 보면
heap = [0]*10
last = 0
enq(2)
enq(5)
enq(7)
enq(3)
enq(4)
enq(6)
while last:
print(deq())
"""
7
6
5
4
3
2
"""
값을 다 넣고, 삭제를 전부 해봤더니 내림차순 정렬된 결과를 얻는다
이것을 heap sort라고 부름
값이 중간중간 추가되거나 삭제되더라도 계속해서 정렬된 결과를 얻고싶다면.. 유용할 수 있다
최대힙을 사용하면 최댓값이 빠져나올테니까 내림차순 정렬이 될거고
최소힙을 사용하면 최솟값이 빠져나올테니까 오름차순 정렬이 된다
8. 최소힙의 삽입, 삭제연산
최대힙의 삽입, 삭제연산을 이해했다면 최소힙의 삽입, 삭제연산을 구현하는건 식은죽 먹기
최소힙의 규칙 "부모 노드 < 자식 노드"만 만족시키도록 바꿔주면 된다
8-1) 최소힙의 삽입연산
##최소힙의 삽입연산
def enq(n):
##마지막 정점번호 + 1
global last
last += 1
#마지막 노드에 값을 넣고
heap[last] = n
##현재 자식은 마지막 노드, 완전 이진트리이므로 부모는 c//2
c = last
p = c//2
##부모 노드가 존재하면서, 부모 > 자식이면 자리를 교환
while p and heap[p] > heap[c]:
heap[p],heap[c] = heap[c], heap[p]
##바꾸고 난 다음에 초기화작업
c = p
p = c//2
8-2) 최소힙의 삭제연산
부모와 자식을 비교할때, 최대힙에서는 두 자식이 존재한다면 더 큰 자식과 비교했는데
최소힙에서는 두 자식중에 더 작은 자식과 비교해야 의미가 있다
##최소힙의 삭제연산
def deq():
global last
##루트원소를 가져온다
tmp = heap[1]
##마지막 원소를 루트 자리에 두고
heap[1] = heap[last]
last -= 1 ##마지막 노드를 삭제하고
##교환을 위해 초기화
p = 1 ##루트부터 시작해서 자리를 찾아가기 시작해야함
c = 2*p ##왼쪽 자식부터 일단 비교를 시작
while c <= last: #자식이 하나라도 존재하면..
##오른쪽 자식도 존재하고, 오른쪽 자식이 왼쪽자식보다 더 작으면
##비교 대상을 오른쪽 자식으로 바꿔준다.
if c+1 <= last and heap[c] > heap[c+1]:
c += 1 ##더 작은 오른쪽 자식으로 비교 대상 바꾸기
if heap[p] > heap[c]: ##부모가 자식보다 크다면
#최소힙 규칙에 어긋나므로 교환
heap[p],heap[c] = heap[c],heap[p]
##계속 바꿔줘야할 수 있으니 부모,자식 초기화
p = c
c = 2*p
else:
break
##반복문을 탈출하면 모든 위치 조정이 완료되었고
return tmp ##루트값 반환
8-3) 힙정렬
최소힙을 사용한 힙정렬 결과는 어떨까?
heap = [0]*10
last = 0
enq(2)
enq(5)
enq(7)
enq(3)
enq(4)
enq(6)
while last:
print(deq())
"""
2
3
4
5
6
7
"""
실제로 내림차순 정렬이 이루어지고 있다
'알고리즘 > 그래프 이론 정복기' 카테고리의 다른 글
| 최소 공통 조상(Lowest Common Ancestor,LCA)문제 기본 해법 배우기1 (0) | 2023.08.07 |
|---|---|
| 컴퓨터로 한붓그리기 하는 방법 - 오일러 경로를 찾는 알고리즘 (0) | 2023.02.19 |
| 트리 응용 알고리즘 몇가지 - 자손, 루트, 조상찾기, 서브트리 부분순회 - (0) | 2022.09.30 |
| 그래프 이론 - 서로소집합(disjoint set) 기본개념1 - (0) | 2022.09.29 |
| 트리 이론 기본편 -중위 순회의 특징 응용하기- (0) | 2022.09.15 |

