1. 완전이진트리 기본 순회 3가지
다음과 같은 완전이진트리에서 전위순회, 중위순회, 후위순회를 구해본다면..?

##노드 번호로 순회함수 정의
##완전이진트리의 왼쪽 자식은 2*v
##오른쪽 자식은 2*v+1
##전위순회
def preorder(v):
if v <= size: ## 노드 번호가 tree의 크기를 벗어나지 않는다면...
print(tree[v],end= ' ')
preorder(2*v)
preorder(2*v+1)
##중위순회
def inorder(v):
if v <= size:
inorder(2*v)
print(tree[v],end = ' ')
inorder(2*v+1)
##후위순회
def postorder(v):
if v <= size:
postorder(2*v)
postorder(2*v+1)
print(tree[v], end = ' ')
##완전이진트리 정의
tree = [0, 'A', 'B', 'C', 'D',' E','F']
size = len(tree)-1
##루트가 1번이라면..
##전위순회
print("전위순회")
preorder(1)
##중위순회
print("중위순회")
inorder(1)
##후위순회
print("후위순회")
postorder(1)
"""
전위순회
A B D E C F 중위순회
D B E A F C 후위순회
D E B F C A
"""
2. 3가지 순회를 한번에 하기
3가지 순회가 전부 필요하다면, 하나의 함수에 한번에 가능하다
당연히 응용하면 2가지만 할수도 있겠지??
##3가지 순회 한번에 하기
def traverse(v):
if v <= size: ##노드 번호가 size를 넘어서지 않는다면
preorder_list.append(tree[v]) ##방문처리
traverse(2*v) ##왼쪽이동
inorder_list.append(tree[v]) ##방문처리
traverse(2*v+1) ##오른쪽이동
postorder_list.append(tree[v])
##완전이진트리 정의
tree = [0,'A','B','C','D','E','F']
size = len(tree) - 1
##순회
preorder_list = []
inorder_list = []
postorder_list = []
##루트가 1번이라면..
traverse(1)
print('전위순회 ',*preorder_list)
print()
print('중위순회 ', *inorder_list)
print()
print('후위순회 ', *postorder_list)
"""
전위순회 A B D E C F
중위순회 D B E A F C
후위순회 D E B F C A
"""
3. 부분순회
항상 1번이 루트라고 생각하고 1번에서만 순회하긴 했는데, 사실 부분 서브트리에서 부분순회만 할수도 있다
그거는 당연히 1번이 루트라면, preorder(2) 이런식으로 하면 되겠지
##부분순회
def traverse(v):
if v <= size:
preorder_list.append(tree[v])
traverse(2*v)
inorder_list.append(tree[v])
traverse(2*v+1)
postorder_list.append(tree[v])
##완전이진트리 정의
tree = [0,'A','B','C','D','E','F']
size = len(tree)-1
##순회
preorder_list = []
inorder_list = []
postorder_list = []
##2번에서 순회
traverse(2)
print('전위순회 ',*preorder_list)
print()
print('중위순회 ', *inorder_list)
print()
print('후위순회 ', *postorder_list)
"""
전위순회 B D E
중위순회 D B E
후위순회 D E B
"""
그림으로 그려보면 다음과 같다
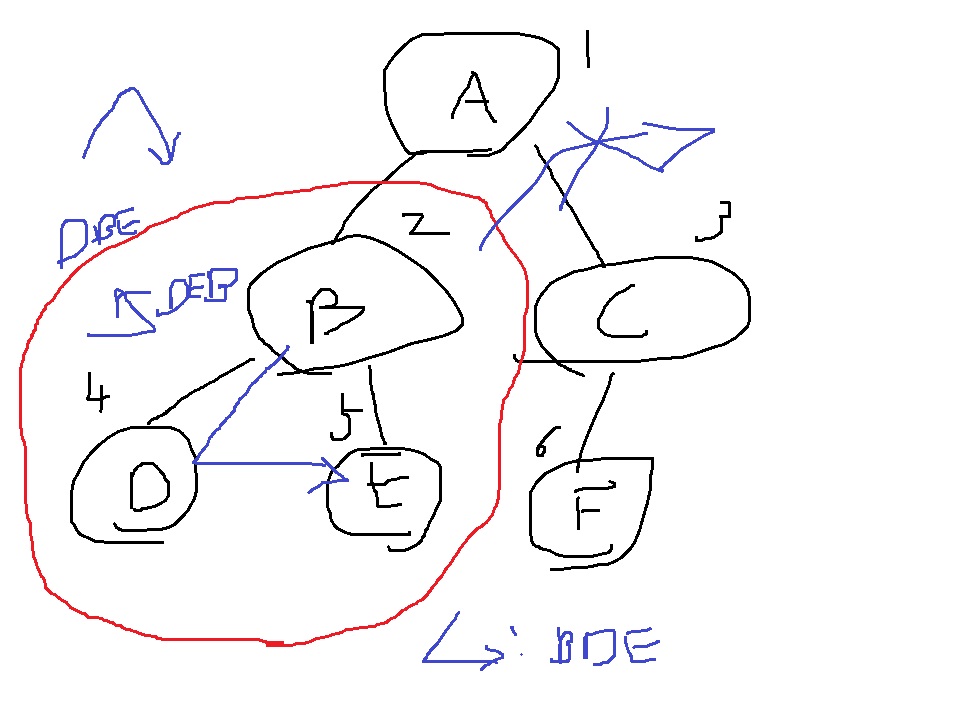
전위순회를 예로 들어 생각해보면,
B에서 시작한다고 해서 B - D - E하고, B로 올라오면, B 밖으로 빠져나갈거라고 생각하는데, 그렇지 않다
부분순회는 그러한 부분트리에서만 순회하게 된다
4. 자손의 개수(후위 부분순회)
어떤 노드의 자손의 개수
혹은 어떤 노드를 루트로 하는 서브트리에 속한 노드의 개수는 어떻게 구할까
위에서 제시한 부분순회를 하면 될 것이다
특정 노드를 기준으로 전위순회하면 모든 자식을 알 수 있으니까, 자기 자신만 빼면 모두 자손이겠지
시간절약을 위해 후위순회해서 마지막 원소인 루트를 빼버리면 모두 자손만 남을듯
##자손의 개수?
def traverse(v):
if v <= size:
traverse(2*v)
traverse(2*v+1)
postorder_list.append(tree[v])
##완전이진트리 정의
tree = [0,'A','B','C','D','E','F','G','H','I','J','K']
size = len(tree)-1
##순회
preorder_list = []
inorder_list = []
postorder_list = []
##2번에서 순회
traverse(2)
print(postorder_list)
print(f'{postorder_list.pop()}의 자손 ', *postorder_list)
"""
['H', 'I', 'D', 'J', 'K', 'E', 'B']
B의 자손 H I D J K E
"""
5. 마지막 방문 노드 출력
이미 위에서 한것이나 마찬가지
순회하면서 방문한 노드를 리스트에 담아서, 리스트의 마지막 원소를 출력하면 되겠지
혹은 리스트에 담기가 싫다면, 하나의 방문 변수에 계속 방문한 값을 갱신해나가면, 마지막에 남은 값이 마지막 방문 노드일것
###마지막 노드
##순회함수 정의
def traverse(v):
global pre,inor,post
if v <= size:
pre = tree[v]
traverse(2*v)
inor = tree[v]
traverse(2*v+1)
post = tree[v]
##완전이진트리 정의
tree = [0,'A','B','C','D','E','F','G','H','I','J','K']
size = len(tree) - 1
##마지막 방문노드
pre = 0
inor = 0
post = 0
##순회시작
traverse(1)
print('전위',pre)
print()
print('중위', inor)
print()
print('후위', post)
"""
전위 G
중위 G
후위 A
"""
6. 루트와 조상 찾기
자식을 인덱스로 하고 부모 번호를 배열에 저장한 트리에서 모든 정점이 1개의 트리에 속한다고 가정하면

루트의 부모는 0번으로 존재하지 않는다
따라서 부모를 저장한 리스트를 순회하여 최초로 0이 나온 index를 찾는다
#입력
#4
#2 1 2 3 1 4 1 5 ##부모-자식
E = int(input())
arr = list(map(int,input().split()))
##간선의 수 + 1 = 정점의 수
V = E + 1
#######
##자식 번호를 인덱스로, 부모 번호를 저장
par = [0] * (V+1)
for i in range(E):
##i = 0이면, 0,1
##i = 1이면, 2,3
##i = 2이면, 4,5,..
p,c = arr[i*2], arr[i*2+1]
par[c] = p
##모든 정점이 1개의 트리에 속한다고하면,
##이 트리의 루트는..?
root = 0
for i in range(1,V+1):
##1번부터 V번 노드까지에서 최초로 부모 노드가 0인 노드가 루트 노드
if par[i] == 0:
root = i
break
print(root)
"""
4
2 1 2 3 1 4 1 5
2
"""
어떤 노드의 조상은 어떻게 찾을 수 있을까..?
특정 i번의 par[i]가 0번이 아니라면, par[i]의 par[par[i]]를 찾고, 이것도 0이 아니라면, 계속 들어가
0이 될때까지 멈추면 만난 노드들이 전부 조상이 된다

###조상을 찾는법
i = 4 ##4번 노드의 조상?
target_list = []
while par[i] != 0:
i = par[i]
target_list.append(i)
print(target_list)
"""
[1,2]
"""'알고리즘 > 그래프 이론 정복기' 카테고리의 다른 글
| 컴퓨터로 한붓그리기 하는 방법 - 오일러 경로를 찾는 알고리즘 (0) | 2023.02.19 |
|---|---|
| 최대힙, 최소힙 직접 구현하기 (0) | 2022.10.02 |
| 그래프 이론 - 서로소집합(disjoint set) 기본개념1 - (0) | 2022.09.29 |
| 트리 이론 기본편 -중위 순회의 특징 응용하기- (0) | 2022.09.15 |
| 트리 이론 기본편4 -이진 탐색 트리 + heap(힙) 간단하게- (0) | 2022.09.13 |

