1. 병합정렬(merge sort)
여러개의 정렬된 자료의 집합을 병합하여 한 개의 정렬된 집합으로 만드는 방식
분할 정복 알고리즘을 활용함
주어진 자료를 최소 단위의 문제까지 나눈 다음에 차례대로 정렬해가면서 최종 결과를 얻어내는 방식
시간복잡도는 O(nlogn)
2. 개요 - 간단한 과정 -
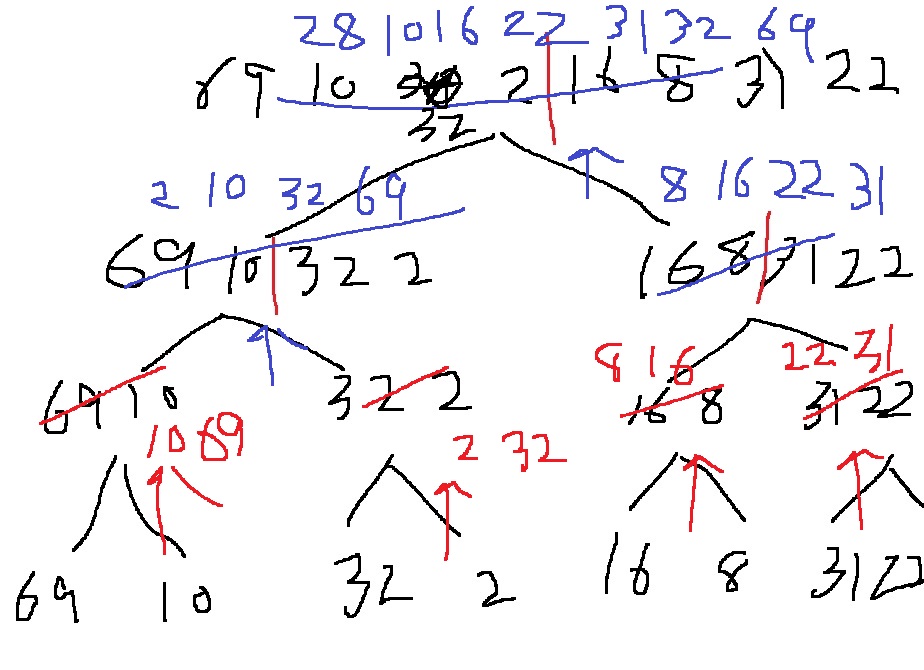
[69,10,30,2,16,8,31,22]를 병합정렬한다면??
2-1) 분할과정
절반씩 자료를 왼쪽, 오른쪽으로 나눠가고 더 이상 쪼갤 수 없을때까지 반복해서 나눈다

2-2) 병합과정
가장 밑단의 왼쪽 부분집합과 오른쪽 부분집합의 원소 크기를 서로 비교하여 정렬하여 병합시키고, 최종 1개로 병합될때까지 반복함
3. 구현
길이가 1이면 정렬하지말고, 바로 return
길이가 1보다 크다면, 왼쪽과 오른쪽을 나눠준다.
mid 공식은 mid = len(list)//2
재귀적으로 left,right를 계속 나눠준다.
left = merge_sort(left)
right = merge_sort(right)
재귀함수가 종료되면, 가장 밑단부터 병합과정을 거친다
##분할과정
def merge_sort(m):
if len(m) == 1: ##길이가 1인 리스트는 정렬할게 없다
return m
##정렬할게 존재하면 왼쪽, 오른쪽으로 나눌 것
##중간의 위치를 구하고
middle = len(m)//2
#left = m[:middle]
#right = m[middle:]
left = []
right = []
##인덱싱 후에 왼쪽,오른쪽에 각각 원소를 넣는다
for x in m[:middle]:
left.append(x)
for x in m[middle:]:
right.append(x)
##재귀적으로, 더이상 나눌 수 없을때까지 나눈다
left = merge_sort(left)
right = merge_sort(right)
##재귀함수가 종료되면, 가장 최하단부터 병합과정을 거친다
return merge(left,right)
다음 병합과정은 왼쪽과 오른쪽의 길이가 남아있다면...?
0번째 원소가 작은 곳의 원소를 pop하여 result에 계속 넣어준다.
그러다보면 어느 한쪽은 없어지는데, 남아있는 쪽의 원소를 계속 0번째부터 pop해서 가져온다
##병합과정
def merge(left,right):
result = []
while len(left) > 0 or len(right) > 0:
if len(left) > 0 and len(right) > 0: ##왼쪽,오른쪽이 모두 남아있는 경우에
if left[0] <= right[0]: ##0번째 원소가 작은 쪽의 원소를 가져온다.
result.append(left.pop(0))
else:
result.append(right.pop(0))
##pop을 하다보니, 왼쪽이나 오른쪽 둘중 하나만 남아있다
##남아있는 쪽의 원소를 0번째부터 차례대로 가져온다
elif len(left) > 0:
result.append(left.pop(0))
elif len(right) > 0:
result.append(right.pop(0))
return result
전체 코드..
##병합과정
def merge(left,right):
result = []
while len(left) > 0 or len(right) > 0:
if len(left) > 0 and len(right) > 0: ##왼쪽,오른쪽이 모두 남아있는 경우에
if left[0] <= right[0]: ##0번째 원소가 작은 쪽의 원소를 가져온다.
result.append(left.pop(0))
else:
result.append(right.pop(0))
##pop을 하다보니, 왼쪽이나 오른쪽 둘중 하나만 남아있다
##남아있는 쪽의 원소를 0번째부터 차례대로 가져온다
elif len(left) > 0:
result.append(left.pop(0))
elif len(right) > 0:
result.append(right.pop(0))
return result
##분할과정
def merge_sort(m):
if len(m) == 1: ##길이가 1인 리스트는 정렬할게 없다
return m
##정렬할게 존재하면 왼쪽, 오른쪽으로 나눌 것
##중간의 위치를 구하고
middle = len(m)//2
#left = m[:middle]
#right = m[middle:]
left = []
right = []
##인덱싱 후에 왼쪽,오른쪽에 각각 원소를 넣는다
for x in m[:middle]:
left.append(x)
for x in m[middle:]:
right.append(x)
##재귀적으로, 더이상 나눌 수 없을때까지 나눈다
left = merge_sort(left)
right = merge_sort(right)
##재귀함수가 종료되면, 가장 최하단부터 병합과정을 거친다
return merge(left,right)
a = [8,5,4,9,1,3,0]
sort_a = merge_sort(a)
print(sort_a)
4. 실전적 구현
근데 위 구현은 딱 봐도 매우 느리다
리스트의 길이가 매우 커지면 list.pop(0)가 그 길이만큼 시간이 걸리니까
그래서 실제 구현에는 인덱스 이동으로 구현한다
구현 원리는 병합시킬려는 왼쪽, 오른쪽 리스트에 대하여
인덱스 포인터를 각각 준비하고
포인터가 가리키는 원소 크기를 비교하여, 작은쪽의 원소를 정렬하고자 하는 리스트의 해당 위치에 집어넣고
집어넣은 쪽의 포인터를 1칸 오른쪽으로 이동한다

10과 2를 비교해서 2가 더 작으니 2를 넣고, 오른쪽의 포인터를 1 증가
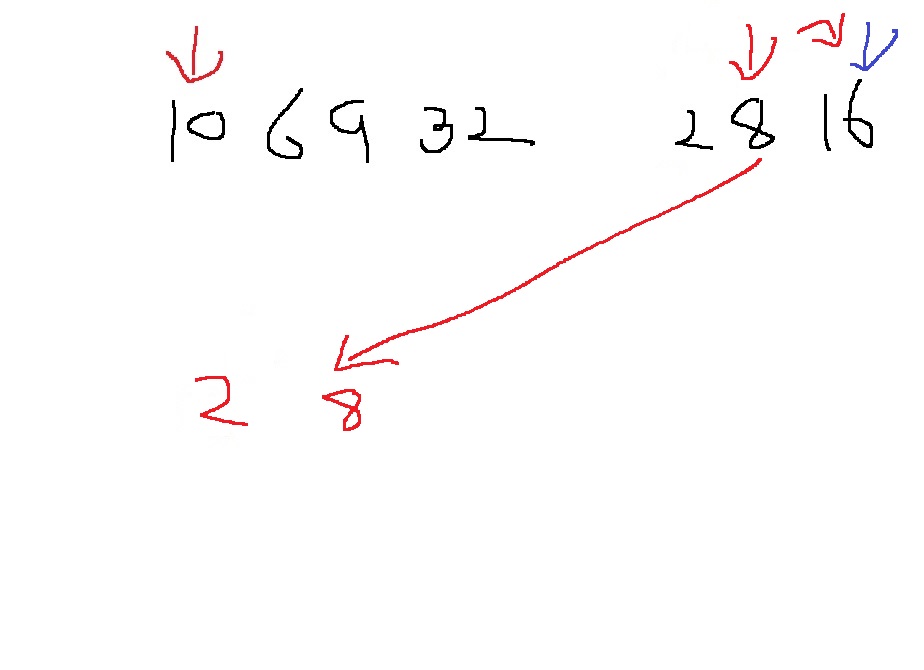
다시 10과 8을 비교하면, 8이 더 작아서, 8을 집어넣고, 오른쪽 포인터를 1 증가

위 과정을 반복하면, 오른쪽 리스트의 포인터는 길이 이상으로 넘어감
그러면 왼쪽 리스트의 원소를 차례대로 집어넣으면 된다

아니 그림이 좀 이상한데??? 아무튼 위와 같은 원리를 코드로 그대로 표현하면 된다
##실전적 구현
##인덱스 이동만으로 아주 빠르게 정렬
def merge_sort(numbers):
##분할과정
n = len(numbers) ##정렬 대상의 리스트 길이를 미리 구해놓는다
if n <= 1:
return ##더 이상 분할할 수 없다
##중간 위치
middle = n//2
##왼쪽, 오른쪽으로 나눈다
left = numbers[:middle]
right = numbers[middle:]
##더 이상 나눌 수 없을때까지 분할
merge_sort(left)
merge_sort(right)
##병합과정
left_ind = 0 ##왼쪽 리스트 포인터
right_ind = 0 ##오른쪽 리스트 포인터
now = 0 ##리스트에 넣을 위치
while left_ind < len(left) and right_ind < len(right): ##왼쪽과 오른쪽이 모두 남아있으면
##왼쪽과 오른쪽 포인터가 가리키는 원소를 비교하여
##작은쪽의 원소를 리스트에 넣고
##작은쪽의 포인터를 오른쪽으로 1칸 이동
##왼쪽이 더 작다
if left[left_ind] <= right[right_ind]:
numbers[now] = left[left_ind]
left_ind += 1
now += 1
else: ##오른쪽이 더 작다
numbers[now] = right[right_ind]
right_ind += 1
now += 1
##포인터가 이동하다보면, 어느 한쪽은 해당 리스트 길이이상으로 포인터가 넘어갈 수 있다
##그래서 한쪽만 리스트 내부에 포인터가 존재한다면..
##그 리스트의 원소를 차례대로 채워넣는다
while left_ind < len(left):
numbers[now] = left[left_ind]
left_ind += 1
now += 1
while right_ind < len(right):
numbers[now] = right[right_ind]
right_ind += 1
now += 1
a = [5,1,2,8,3,4,9]
merge_sort(a)
print(a)
[1, 2, 3, 4, 5, 8, 9]
근데 이게 어떻게 분할되고, 정렬되는지 재귀라서 머리로 파악하기는 힘들 수 있어
그렇다면 중간에 분할된 리스트와 병합되는 리스트를 출력해서 비교해보면 된다

5,1,2와 8,3,4,9로 먼저 분할되었던 리스트가 아래에서 정렬하고 병합시켰더니
마지막에 왼,오 부분을 보면 [1,2,5], [3,4,8,9] 상태로 비교하는 것을 볼 수 있다
전부 분할하고 마지막부터 병합과정에서, 분할되었던 리스트들이 정렬상태로 바뀌어서 진행되고 있다는 것을 볼 수 있다
5. 연습문제
2751번: 수 정렬하기 2
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 절댓값이 1,000,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.
www.acmicpc.net
수의 개수가 100만개라서 O(nlogn)의 정렬 알고리즘을 사용해야 풀 수 있는 문제
병합정렬과 퀵정렬이 있는데
퀵정렬은 이미 정렬된 수열은 잘 정렬시키지 못한다는 특징이 있다.
최악의 경우 $O(n^{2})$이라는 소리
그래서 병합정렬로 정렬하면 된다
6. 풀이
from sys import stdin
def merge_sort(numbers):
n = len(numbers)
if n <= 1:
return
mid = n//2
left = numbers[:mid]
right = numbers[mid:]
merge_sort(left)
merge_sort(right)
left_ind = 0
right_ind = 0
now = 0
while left_ind < len(left) and right_ind < len(right):
if left[left_ind] <= right[right_ind]:
numbers[now] = left[left_ind]
left_ind += 1
now += 1
else:
numbers[now] = right[right_ind]
right_ind += 1
now += 1
while left_ind < len(left):
numbers[now] = left[left_ind]
left_ind += 1
now += 1
while right_ind < len(right):
numbers[now] = right[right_ind]
right_ind += 1
now += 1
n = int(stdin.readline())
n_list = []
for _ in range(n):
a = int(stdin.readline())
n_list.append(a)
merge_sort(n_list)
for i in n_list:
print(i)
-------------------------------------------------------------------------------------------------------------------------------------------------------------
7. 최신판
속도는 위와 사실 비슷한데..
조금 더 직관적이고 깔끔하게 구현했다
이걸로 기억해두면 좋을듯
from sys import stdin
def merge(A,start,mid,end):
merged_list = [0]*(end-start+1) #병합된 배열
#분할된 배열은 A[start,....,mid], A[mid+1,....,end]
i = start #분할된 첫번째 배열의 시작 index
j = mid+1 #분할된 두번째 배열의 시작 index
k = 0 #병합된 배열의 시작 index
#분할된 두 배열이 각각 가리키는 index에서 원소 크기를 비교함
#더 작은 원소를 병합된 배열에 집어넣고, 집어넣은 배열의 index를 1칸 오른쪽으로 이동
#집어넣었을경우, 다음 위치로 집어넣기 위해 집어넣어야할 위치 k도 1칸 오른쪽 이동
while i <= mid and j <= end:
if A[i] > A[j]:
merged_list[k] = A[j]
k += 1
j += 1
else:
merged_list[k] = A[i]
k += 1
i += 1
#반복문이 끝나면 둘 중 하나의 분할된 배열의 모든 원소는 병합된 배열에 들어감
#들어가지 않은 둘 중 하나의 배열의 나머지 원소를 모두 집어넣는 과정
while i <= mid:
merged_list[k] = A[i]
i += 1
k += 1
while j <= end:
merged_list[k] = A[j]
j += 1
k += 1
#마지막으로 정렬된 상태를 원래 배열에 넣어주는 과정
for s in range(start,end+1):
A[s] = merged_list[s-start]
def merge_sort(A,start,end):
if start == end:
return
mid = start + (end - start)//2
merge_sort(A,start,mid)
merge_sort(A,mid+1,end)
merge(A,start,mid,end)
n = int(stdin.readline())
A = [int(stdin.readline()) for _ in range(n)]
merge_sort(A,0,n-1)
print('\n'.join(map(str,A)))'알고리즘 > 정렬 알고리즘' 카테고리의 다른 글
| 거품이 올라오는 것처럼 정렬하는 bubble sort(버블 정렬) (0) | 2022.10.09 |
|---|---|
| 가장 원시적인 정렬 알고리즘인 selection sort(선택 정렬) (0) | 2022.10.09 |
| 조건을 만족할때 매우 빠른 정렬 - counting sort (0) | 2022.08.11 |
| 다중 정렬을 단일 정렬로 바꿔보자 (0) | 2022.01.25 |
| dictionary를 정렬하는 방법? (0) | 2021.11.23 |

