1. 정렬(sorting)
데이터를 특정한 기준에 따라서 순서대로 나열하는 것
프로그램에서 데이터를 가공할 때 오름차순이나 내림차순 등 대부분 어떤 식으로든 정렬해서 사용하는 경우가 많기에, 정렬 알고리즘은 프로그램을 작성할 때 가장 많이 사용되는 알고리즘 중 하나
정렬 알고리즘으로 데이터를 정렬하면, 이진 탐색(binary search)이 가능해진다. 즉, 이진 탐색의 전처리 과정이기도 하다.
정렬을 공부하다보면 알고리즘의 효율성을 쉽게 이해할 수 있어
상황에 적절하지 못한 정렬 알고리즘을 이용하면, 당연히 프로그램은 비효율적으로 동작하면서, 필요 이상으로 시간을 많이 소요
여기 숫자 카드 10장이 있다.
7, 5, 9, 0, 3, 1, 6, 2, 4, 8
어떻게 이 카드를 정렬할 수 있을까? 보통은 카드를 빠르게 훑고 숫자가 0부터 9까지로 구성된 걸 눈치챈 다음에 카드를 0부터 9까지 순차적으로 나열할 것
이러한 과정에서 우리의 뇌는 우리도 모르게 데이터의 규칙성을 파악한다.
하지만 우리에게 쉽다고, 컴퓨터에게도 쉬운 일은 아니다.
컴퓨터는 인간과 다르게 데이터의 규칙성을 직관적으로 알 수 없으며, 어떻게 정렬을 수행할지에 대한 과정을 소스코드로 구체적으로 명시해야한다.
2. 선택 정렬(selection sort)
데이터가 무작위로 여러 개 있을때, 이 중에서 가장 작은 데이터를 선택해 맨 앞에 있는 데이터와 바꾸고, 그 다음 작은 데이터를 선택해 앞에서 두번째 데이터와 바꾸는 과정을 반복하면 어떨까?
이러한 방법을 "매번 가장 작은 것을 선택한다"는 의미에서 선택 정렬(selection sort)이라고 부른다.
가장 작은 것을 선택해서 앞으로 보내는 과정을 반복해서 수행하다 보면, 전체 데이터의 정렬이 이루어진다.
3. 예시를 통해 이해하는 선택 정렬
다음과 같은 데이터를 정렬한다고 생각해보자.
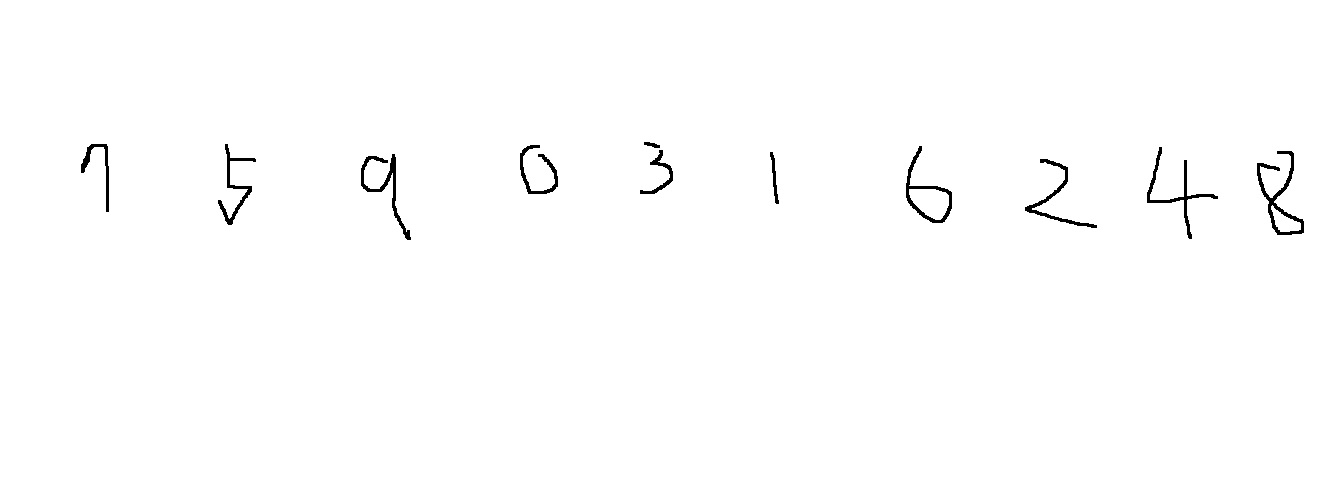
초기 단계에서는 모든 데이터가 정렬되어 있지 않으므로, 전체 데이터 중에서 가장 작은 데이터를 선택한다.
따라서 0을 선택해 맨 앞에 있는 데이터 7과 바꾼다

이제 정렬된 첫번째 0은 제외하고, 나머지 데이터 중에서 가장 작은 데이터인 1을 선택해서 처리되지 않은 데이터 중 가장 앞에 있는 5와 바꾼다

마찬가지로 계속해서 과정을 반복한다.
정렬된 데이터를 제외하고 9~8까지에서 가장 작은 데이터인 2를 선택한다.
이것을 정렬되지 않은 데이터에서 가장 앞에 있는 9와 바꾼다
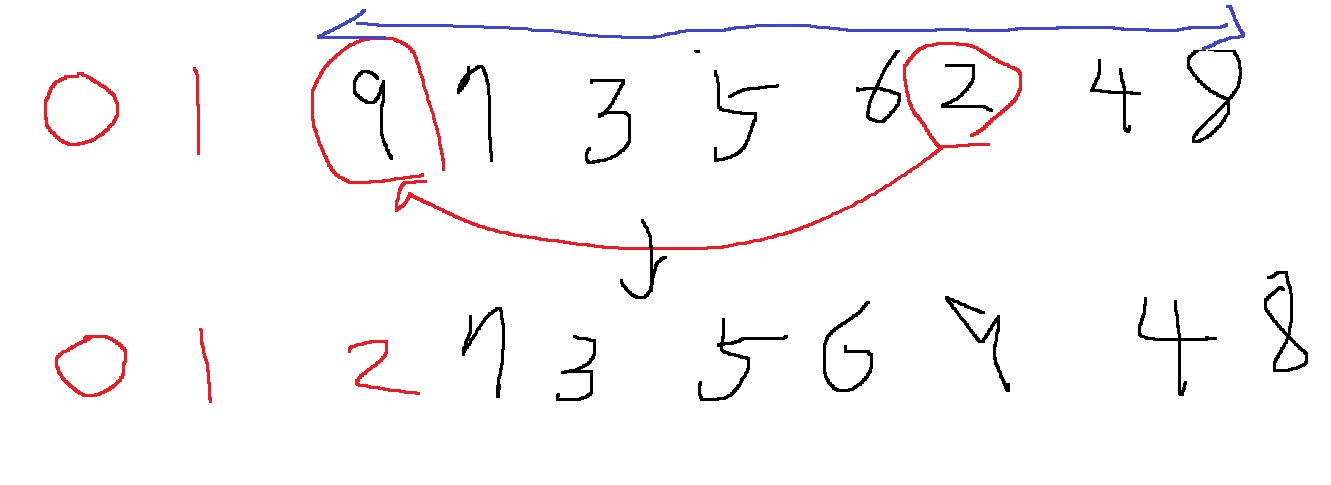
위 과정을 계속 반복하면, 7~8중에서 가장 작은 3을 정렬되지 않은 데이터 중에서 가장 앞에 있는 7과 바꾸고,
다시 7~8에서 가장 작은 4를 정렬되지 않은 데이터 중에서 가장 앞에 있는 7과 바꾸고
다시 5~8에서 가장 작은 5를 정렬되지 않은 데이터 중에서 가장 앞에 있는 5와 바꾸고,
다시 6~8에서 가장 작은 6을 정렬되지 않은 데이터 중에서 가장 앞에 있는 6과 바꾸고,
다시 9~8에서 가장 작은 7을 정렬되지 않은 데이터 중에서 가장 앞에 있는 9와 바꾸면..

마지막으로 남은 9와 8중에서 가장 작은 8을, 정렬되지 않은 데이터에서 가장 앞에 있는 9와 바꾸면 최종적으로 정렬이 완료된다.
데이터의 개수가 n=10일때, 0~8까지 n-1=9개의 데이터를 선택하여 맨 앞으로 보내는 과정을 반복했다
이처럼 선택정렬은 가장 작은 데이터를 앞으로 보내는 과정은 n-1번 반복하면 정렬이 완료된다는 것을 알 수 있다.
3. 구현 예시
##선택정렬
array = [7,5,9,0,3,1,6,2,4,8]
n = len(array) ##배열의 길이
for i in range(n):
min_index = i ##현재 단계에서 가장 작은 원소의 인덱스
for j in range(i+1,n): ##i번 말고 나머지 중에서 가장 작은 원소를 찾는 과정
if array[min_index] > array[j]: ##i번 원소보다 더 적은 j번 원소를 찾으면..
min_index = j ##최솟값을 j번이라고 갱신
##현재 단계에서 최솟값과 i번 원소를 교체
array[i],array[min_index] = array[min_index],array[i]
print(array)
"""
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
"""
n-1번 반복한다면서 왜 n번 반복하냐??
어차피 코드를 보면 마지막 단계에서는 아무것도 수행되지 않는다
그리고 파이썬에서는 리스트 내에서 두 원소의 위치를 바꾸는 작업(swap)을 아주 간단하게 수행할 수 있다
#두 원소의 위치를 바꾸기
array = [3,5]
array[0],array[1] = array[1],array[0]
print(array)
"""
[5,3]
"""
4. 시간복잡도
선택정렬은 n-1번만큼 가장 작은 수를 찾아서 맨 앞으로 보내야한다.
또한 매번 가장 작은 수를 찾기 위해 비교 연산을 수행해야한다.
구현 방식에 따라 약간의 차이는 있을 수 있지만, 위와 같이 구현했을때 연산 횟수는 N+(N-1)+(N-2)+...+2이고,
근사적으로 N(N+1)/2번의 연산을 수행한다.
그러므로 빅오 표기법으로 $O(N^{2})$의 시간 복잡도가 소요된다.
직관적으로는 각각 n번을 반복하는 2중 for문이 사용되어서 $O(N^{2})$이라고 이해할 수 있다
만약 정렬해야할 데이터의 개수가 100배 늘어난다면, 이론적으로는 수행 시간이 10000배로 늘어난다.
선택 정렬을 이용하는 경우 데이터의 개수가 10000개 이상이면 정렬 속도가 급격히 느려져서 다른 정렬 알고리즘에 비해 매우 비효율적이다.
하지만 "특정한 리스트에서 가장 작은 데이터를 찾는 일"은 기본적인 테크닉이므로 선택 정렬의 소스코드에 익숙해질 필요가 있다
5. 연습문제
2750번: 수 정렬하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수 주어진다. 이 수는 절댓값이 1,000보다 작거나 같은 정수이다. 수는 중복되지 않는다.
www.acmicpc.net
$O(n^{2})$의 정렬 알고리즘으로 해결할 수 있는 정렬 문제
from sys import stdin
n = int(stdin.readline())
array = []
for _ in range(n):
i = int(stdin.readline())
array.append(i)
for i in range(n):
min_index = i
for j in range(i+1,n):
if array[min_index] > array[j]:
min_index = j
array[i],array[min_index] = array[min_index],array[i]
for num in array:
print(num)'알고리즘 > 정렬 알고리즘' 카테고리의 다른 글
| 필요한 위치에 삽입하면서 정렬하는 삽입정렬(insertion sort) (0) | 2022.10.09 |
|---|---|
| 거품이 올라오는 것처럼 정렬하는 bubble sort(버블 정렬) (0) | 2022.10.09 |
| 병합 정렬(merge sort) 알고리즘 파헤치기 (0) | 2022.09.28 |
| 조건을 만족할때 매우 빠른 정렬 - counting sort (0) | 2022.08.11 |
| 다중 정렬을 단일 정렬로 바꿔보자 (0) | 2022.01.25 |

