1. 이상치란?
데이터 중 일반적인 데이터와 크게 다른 데이터를 의미함
모델 성능에 큰 영향을 줄 수 있어 조심히 접근해야함

위의 왼쪽에는 상관관계가 0.95로 계산되는데 이상해보이는 3개 제거하고 나니 실제로는 랜덤하게 흩뿌려진 데이터 분포를 나타냄
아래의 그림에서 왼쪽을 보면 깔끔하게 상관관계를 보이는 데이터 분포
그런데 이상한 데이터가 추가되고나니 오른쪽처럼 상관관계가 약간 더러워짐?
2. Z score
Z score로 이상치를 탐지할 수 있는데 관측치 X에 대해 이들의 평균이 $\mu$, 표준편차가 $\sigma$이면
특정 $i$번째 관측치 $X_{i}$의 Z score란 $$Z_{i} = \frac{X_{i} - \mu}{\sigma}$$로 구해지고 이것은 N(0,1)을 따른다.
정규분포의 특징은 평균 $\mu$에서 1표준편차 이내에 68%가 몰려있고
2표준편차 이내에 95%가 몰려있고 3표준편차 이내에 99%가 몰려있다는 특징이 있다
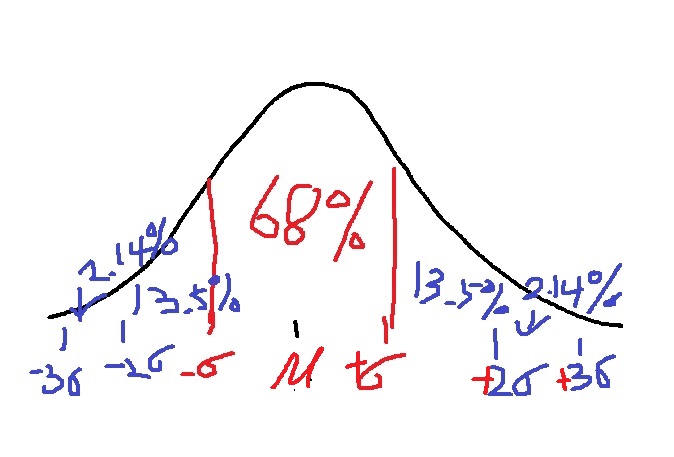
그러므로 Z score는 N(0,1)을 따르니까 관측치의 Z값이 3이상이면(평균=0,표준편차=1)
상당히 낮은 확률로 출현하는 이상치라고 생각할 수 있다
물론 어느정도를 기준으로 잡을지는 사람마다 다를 수 있다
3. IQR
IQR은 box plot을 이용해서 이상치를 판단하는 방법이다.
3사분위수와 1사분위수의 차이 IQR=Q3-Q1으로 구한다
(Q1-1.5IQR, Q3+1.5IQR) <안울타리> 밖에 있고 (Q1-3IQR,Q3+3IQR) <바깥울타리>안에 있는 값을 보통이상점(아래 그림에서 초록색 동그라미 점)
(Q1-3IQR,Q3+3IQR) 밖에 있는 값을 극단이상점(아래 그림에서 파란색 x표시 점)이라고 부름
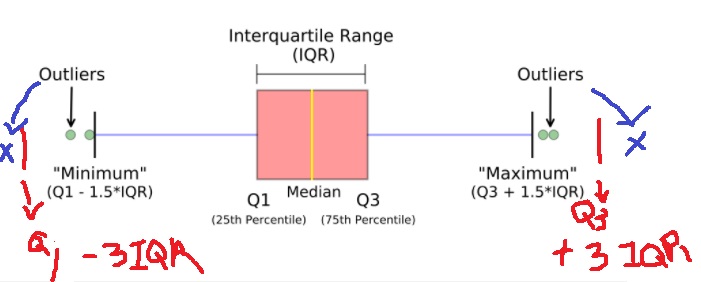
안울타리 (Q1-1.5IQR,Q3+1.5IQR)내에서 최솟값과 최댓값을 위에서 Minimum, Maximum으로 표시함
4. 이상치를 처리할 때 고려사항
정성적으로 이상치가 왜 발생했고 그것이 어떤 의미를 가지는 지 생각해보면 어떻게 처리할 지 감이 올 수 있음
모델의 성능 측면에서 train과 test set을 고려하여 이상치 분포가 동일하다면
train에서 이상치를 삭제할 경우 오히려 모델의 성능이 떨어질 수 있음

위 그림은 아파트 건축년도와 아파트 가격 사이의 관계를 나타낸 그림으로 최근에 건축된 아파트일수록 가격이 높은 경향을 보인다
그런데 특이하게 1970년도 쯤에 건축된 아파트 가격이 상당히 높다
재개발된 아파트거나 재건축된 아파트일 수 있으니 만약 feature에 재개발이나 재건축여부를 추가한다면 다른 경향을 보일 수 있다.

위 그림은 파란색은 train 분포이고 노란색은 test 분포이며 빨간색은 z score로 탐지한 이상치이다.
test에는 빨간색 이상치와 비슷하게 된 부분이 없으니 제거하고 예측 error를 계산해보면
제거하기 전에는 19.86이었다가 제거 후에는 18.42로 성능이 향상
'정형데이터' 카테고리의 다른 글
| cross validation out of fold prediction (0) | 2023.12.07 |
|---|---|
| time series data의 cross validation에 대한 여러가지 고찰 (0) | 2022.06.28 |
| 정형데이터에서 결측치를 처리하는 방법 (0) | 2022.06.24 |
| 연속형 변수를 전처리하는 방법은 무엇이 있고 왜 전처리를 해야하는가? (0) | 2022.06.19 |
| 범주형 변수를 전처리하는 방법의 모든 것 (0) | 2022.05.26 |

