1. 데이터 전처리란?
머신러닝 모델에 데이터를 입력할 수 있도록 적절하게 처리하는 과정
EDA를 위해 데이터 구조를 바꿔서 처리하는 것도 하나의 전처리 과정
EDA 목적이나 모델에 입력데이터를 어떻게 넣어줄 것인가에 따라 달라진다
EDA에서 어떤 부분을 찾고싶은가에 따라서도 달라짐
선형모델이냐 트리모델이냐 딥러닝모델이냐에 따라서도 달라짐
데이터 전처리도 정답이 없지만 어느정도 기본은 있다
머신러닝 모델에 데이터를 입력하기 위한 과정이라는 것을 염두에 두고
연속형, 범주형을 처리 & 결측치 처리 & 이상치 처리
2. 예시로 이해하는 연속형 변수 전처리
sklearn에 있는 boston data
506개의 데이터 포인트, 13개의 변수
CHAS만 범주형이고 나머지는 연속형
target은 집값의 중위수라는데?

3. scaling
데이터의 단위나 분포를 변경하는 것
선형기반 모델인 선형회귀나 딥러닝의 경우 변수들 간 스케일을 맞추는 것은 필수적인 작업
3-1) 값의 scale만 바꾸는 방법
min max scaling은 각 데이터 $X_{i}$에 전체 데이터의 min을 빼주고 max와 min의 차이로 나눠주는 방법
standard scaling은 데이터 x에 전체 데이터의 평균을 빼주고 표준편차로 나눠줌
robust scaling은 각 데이터 $X_{i}$에 중위수를 빼주고 IQR로 나눠줌
여기서 IQR은 3사분위수에서 1사분위수를 빼서 구함
Robust scaling이 이상치에 덜 영향을 받는다고 함
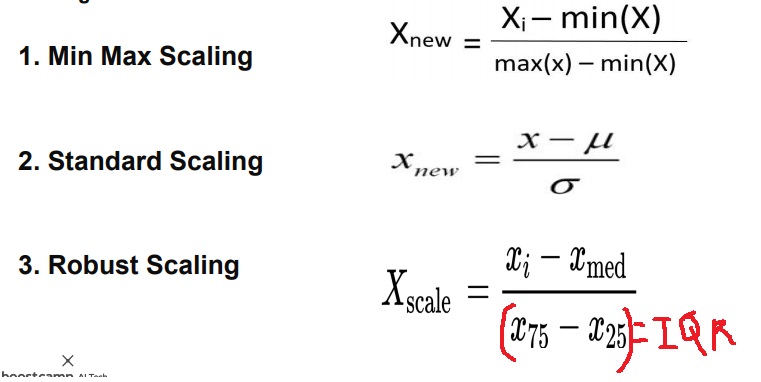
train 80%, test 20%로 임의로 나누고 선형모델을 적합시킴
아래 그림에서 x축은 선형모델의 feature이고 y축은 해당 feature에 대응하는 계수값

min max scaling하면 std error가 26.23이고 age의 계수가 매우 작음
age에 10^(-6)을 곱하면 상당히 커짐 std error는 26.23으로 거의 비슷(끝자리가 조금 다르긴함…)
age에 10^(10)을 곱하면 그냥 안보임. 심지어 error는 33.4로 상승
scaling에 따라서 계수에 의한 모델의 해석 차이가 생기며 그 성능도 영향이 있어 적절한 방법을 선택해야한다
3-2) scale과 분포를 전부 변경하는 방법
log transformation은 전부 양수인 값의 분포가 왼쪽으로 치우칠 때 로그를 취해주면 정규분포에 가깝게 변경시킬 수 있다는 방법
음수면 log를 취할 수 없거든
변환된 분포에서 exponential을 취하면 역변환시킬수도 있다고?

3-3) quantile transformation
https://deepdata.tistory.com/83
분위수 변환(quantile transformation)
1. quantile transformation의 이론적인 설명 주어진 데이터 $x _{1},x _{2} ,...,x _{n}$의 분포를 그려보니 다루기 힘들거나 마음에 안들어서 분포를 변환할 필요가 있다고 합시다. 주어진 데이터 $x _{1},x _{2..
deepdata.tistory.com
데이터 분포를 원하는 분포로 바꾸고자 할 때 사용하는 방법
보통은 uniform이나 normal distribution으로 바꾼다
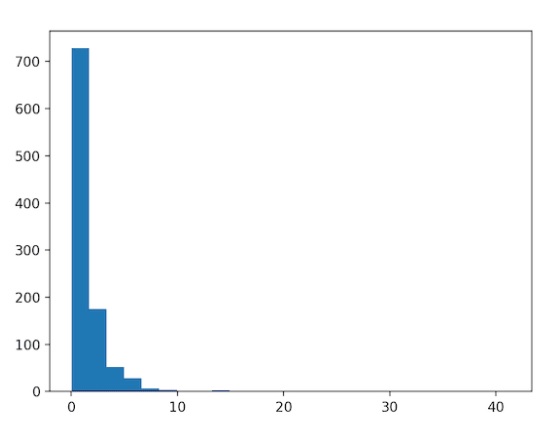
주어진 데이터 분포가 위와 같을 때 왼쪽으로 치우쳐진 분포는 다루기 까다롭다
다음과 같은 이론에 기반함
“연속형 확률변수 X가 a<x<b에서 단조증가함수인 F(x)를 cumulative distribution function으로 가질 때 확률변수 Y=F(X)는 U(0,1)을 따른다.”
“Y의 분포가 U(0,1)이고 a<x<b의 공간 위에서 단조증가함수 F(x)가 F(a)=0, F(b)=1을 갖는 연속형 cumulative distribution function이라고 하면, 연속형 확률변수 $X=F^{-1}(Y)$는 F(x)를 cumulative distribution function을 가진다.”
첫번째 정리에 기반하여 현재 데이터 값 x에 대해 분포함수의 추정량인 F(x)를 구함
그러면 F(x)는 uniform distribution U(0,1)을 따른다고 알려짐
그리고 이 값을 원하는 분포, 예를 들어 Normal distribution의 분포함수인 $\Phi(X)$의 역함수인 quantile function $\Phi^{-1}(X)$에 집어 넣은 $\Phi^{-1}(F(x))$를 구함
그러면 x를 $\Phi^{-1}(F(x))$에 mapping 시키면 normal distribution으로 변환한 것임

log transformation은 왼쪽으로 치우쳐진 분포에 주로 사용하는데
quantile transformation은 어떠한 분포가 들어와도 바꿀 수 있다는 점이 차이이다.
4. 분포를 바꿀 때 얻을 수 있는 효과
주어진 데이터 feature와 target과의 관계를 더욱 직접적으로 변환시켜줌

왼쪽은 LSTAT 분포 오른쪽은 quantile transformation 후 LSTAT 분포
아래 그림은 LSTAT과 target 변수와의 scatter plot
위 그림에서 LSTAT의 분포가 quantile transformation후에 정규분포 형태로 바뀜
target과의 scatter plot으로 원래 상관관계가 -0.74였던 것이 -0.79로 더욱 상관성이 있어짐
이렇게 transformation을 하면 feature와 target과의 상관성을 더욱 높여주어 모델의 성능 향상에 기여할 수 있다
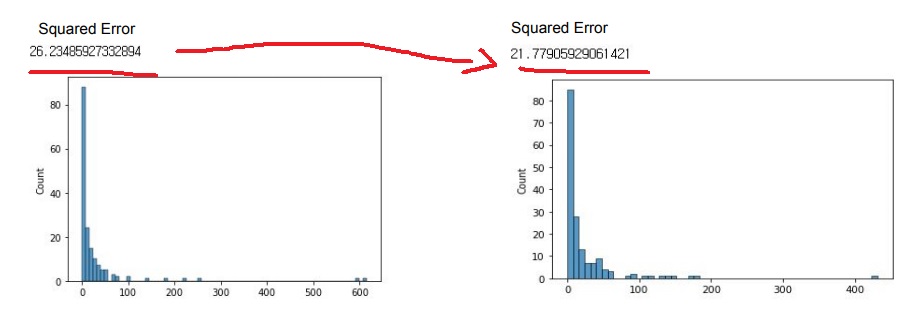
왼쪽은 target과 상관이 높은 feature를 뽑아 선형모델을 만들어 예측값의 분포를 구해본 것
오른쪽은 quantile transformation을 사용하여 모델 예측값의 분포를 구함
적절한 분포 변환이 성능 향상에 기여할 수 있다는 사실을 알 수 있다.
5. binning
연속형 데이터를 적절히 구간으로 나눠 범주형 데이터로 변경하는 방법
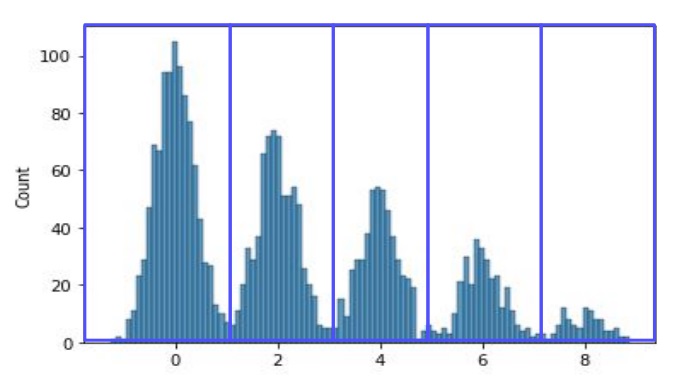
현재 데이터 분포가 위와 같이 눈으로 봐도 구분하기 쉬울 정도로 다봉우리형 분포
그런데 연속형으로 그냥 두면 봉우리 사이 사이에 의미 없는 정보들이 걸릴 수 있어
이것은 tree 모델을 사용하면 overfitting을 발생시킨다고 함
그래서 binning을 이용한 구간 구분으로 범주형으로 변환하여 overfitting을 조금 해소할 수 있음
심지어 선형모델의 경우 해석이 용이할 수 있음
'정형데이터' 카테고리의 다른 글
| 데이터 전처리 - 이상치를 처리하는 방법의 기초 (0) | 2022.06.26 |
|---|---|
| 정형데이터에서 결측치를 처리하는 방법 (0) | 2022.06.24 |
| 범주형 변수를 전처리하는 방법의 모든 것 (0) | 2022.05.26 |
| 회귀문제에서 사용하는 decision tree (0) | 2021.12.15 |
| 연속형 변수를 사용한 decision tree (0) | 2021.12.14 |

