1. 문제
https://programmers.co.kr/learn/courses/30/lessons/12914
코딩테스트 연습 - 멀리 뛰기
효진이는 멀리 뛰기를 연습하고 있습니다. 효진이는 한번에 1칸, 또는 2칸을 뛸 수 있습니다. 칸이 총 4개 있을 때, 효진이는 (1칸, 1칸, 1칸, 1칸) (1칸, 2칸, 1칸) (1칸, 1칸, 2칸) (2칸, 1칸, 1칸) (2칸, 2
programmers.co.kr
효진이는 멀리 뛰기를 연습하고 있습니다. 효진이는 한번에 1칸, 또는 2칸을 뛸 수 있습니다.
칸이 총 4개 있을 때, 효진이는
(1칸, 1칸, 1칸, 1칸)
(1칸, 2칸, 1칸)
(1칸, 1칸, 2칸)
(2칸, 1칸, 1칸)
(2칸, 2칸)
의 5가지 방법으로 맨 끝 칸에 도달할 수 있습니다. 멀리뛰기에 사용될 칸의 수 n이 주어질 때, 효진이가 끝에 도달하는 방법이 몇 가지인지 알아내, 여기에 1234567을 나눈 나머지를 리턴하는 함수, solution을 완성하세요.
예를 들어 4가 입력된다면, 5를 return하면 됩니다.
2. 제한사항
n은 1이상, 2000이하인 정수
3. 예시

4. 나의 풀이
이 문제의 핵심은 결국 n을 1또는 2의 합으로 분해하고 이들을 일렬로 배열하는 수만큼 구하는 것이다.
그러면 1또는 2의 합으로 어떻게 분해해야하냐?
----------------------------------------------------------------------------------
알고리즘적 사고로 생각을 하는 것이다.
2가 0개인 경우, 1은 n개가 있어야하고
2가 1개인 경우, 1은 n-2개가 있어야하고
2가 2개인 경우, 1은 n-4개가 있어야하고
...
----------------------------------------------------------------------------------그러면 for문으로 2가 0부터 순회하면 될 것인데
2의 최댓값은 몇개가 있어야할까?
조금만 생각해보면 2 * a = n이 되는 a가 2의 최댓값이니까.. 결국 n을 2로 나눈 몫이 2의 개수의 최댓값이 된다
def solution(n):
answer = 0
max_two = divmod(n,2)[0]
for two in range(max_two+1):
one = n - (2*two)
n을 2로 나눈 몫은 divmod(n,2)를 하면 (몫,나머지)로 나오니까 몫은 divmod(n,2)[0]으로 구할 수 있다
그러면 2의 개수의 최댓값을 max_two라 하고 0부터 순회를 한다
그럴때 1의 개수 one = n- (2*two)로 구할 수 있을 것이다
그러면 1의 개수와 2의 개수가 구해졌으니까 이제 이들을 일렬로 배열하는 수를 구하면 된다
여러 방법을 생각해보자
가장 먼저 1의 개수와 2의 개수만큼 리스트를 구성하고 collections의 permutations로 모든 permutation을 구하고 len으로 길이를 구하면 된다
for two in range(max_two+1):
one = n - (2*two)
answer += len(set(permutations([1]*one+[2]*two)))
return (answer % 1234567)
근데 이제 이렇게하면 당연하지만 너무 오래걸린다는게 문제다
n의 최댓값이 2000인데 2000을 넣으면 시간초과난다
다른 방법은 순열의 수를 구하면 되는데 '같은 것이 있는 순열'의 수를 이용하면 된다
"n개의 요소에서 a개의 같은 것과 b개의 같은 것이 있는 경우 이들의 순열의 수는 $$\frac{n!}{a!*b!}$$"
from math import factorial
for two in range(max_two+1):
one = n - (2*two)
answer += int(factorial(one+two)/(factorial(one)*factorial(two)))
return (answer % 1234567)
factorial을 구하는 가장 빠른 방법중 하나는 math에서 factorial 함수를 이용하는 것
int로 바꾼 이유는 /의 결과가 실수인데 방법의 수를 구하니까 정수로 변환하고 싶어서 그렇다
참고로 조합의 수, 순열의 수도 itertools의 combinations, permutations의 len으로 구하는게 아니라
math의 함수를 이용할 수 있다


아무튼 이렇게 하면 문제가 n=2000에서 overflow error가 뜬다
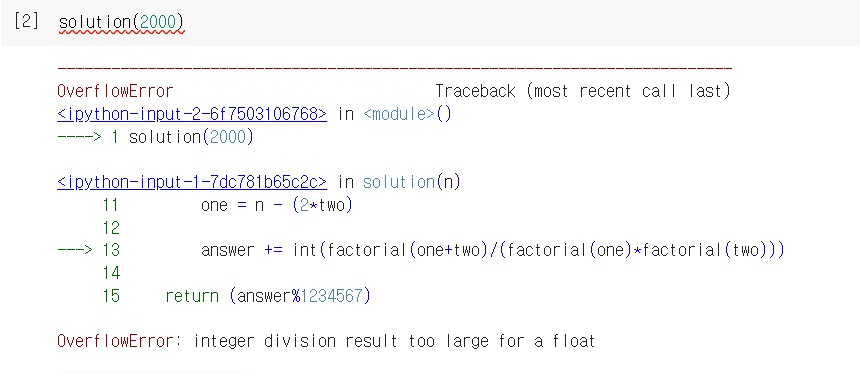
처음에는 꼼수?를 발휘해서 $\frac{n!}{a!*b!}$에서 a>b이면 $\frac{n*n-1*n-2*...*(a+1)}{b!}$,
a<b이면 $\frac{n*n-1*n-2*...*(b+1)}{a!}$ 이런 느낌으로 미리 계산한다음에 factoral을 구하면 달라질까? 이런 생각을 해봄
for two in range(max_two+1):
one = n - (2*two)
count = 1
if one >= two:
for a in range(one+1,one+two+1):
count = count * a
answer += count/factorial(two)
else:
for a in range(two+1,one+two+1):
count = count * a
answer += count/factorial(one)
return (answer % 1234567)하지만 이래도 overflow가 일어나는건 똑같다
왜 그런가 알아봤는데
파이썬이 int에서는 overflow가 발생하지 않도록 설계되어있는데 float에서는 그렇지 않다는 것이 문제였다
/의 결과는 float를 반환하는데 분자나 분모가 너무 커버리면 float 자리수가 너무 커버려서 overflow가 난다
그러면 이걸 어떻게 해결해야하냐?
어차피 '같은 것이 있는 복수순열의 수' $\frac{n!}{a!*b!}$는 결과가 정수라는 점이다
나누어 떨어지지 않을리가 없다는 점이다
그러니까 /으로 하나 //으로 하나 결과는 동일하다
그렇지만 파이썬이 big int는 지원하므로 //으로 하면 overflow가 발생하지 않는다
def solution(n):
from math import factorial
answer = 0
max_two = divmod(n,2)[0]
for two in range(max_two+1):
one = n - (2*two)
answer += factorial(one+two)//(factorial(one)*factorial(two))
return (answer % 1234567)
혹은 위에서 썼던 방법으로 일부를 미리 계산하고 나서 계산하면 조금 더 빠르다
def solution(n):
from math import factorial
answer = 0
max_two = divmod(n,2)[0]
for two in range(max_two+1):
one = n - (2*two)
count = 1
if one >= two:
for a in range(one+1,one+two+1):
count = count * a
answer += count//factorial(two)
else:
for a in range(two+1,one+two+1):
count = count * a
answer += count//factorial(one)
return (answer % 1234567)
5. 되돌아보기
핵심을 잘 파악했다
n을 1과 2의 합으로 분해하고.. 이들의 순열의 수 구하기
1과 2의 합으로 어떻게 분해할까? 알고리즘적으로 생각하자
'2가 0일때 1은 n개, 2가 1일때 1은 n-2개... 이렇게 순회한다' 생각 상당히 잘했다
그런데 복수순열의 수 공식이 생각이 안나더라.. 고등학교때 배운 순열 조합중에 중요한거 복습 다시 한번 해야겠지?
big int는 지원하지만 big float는 지원하지 않는다
어차피 복수순열의 수는 정수니까 /으로 계산하나 //으로 계산하나 결과는 같은데 타입만 다르다
상당히 생각 잘했다
참고
https://www.acmicpc.net/board/view/21217
글 읽기 - 파이썬 코드 런타임 에러 이유가 뭘까요?
댓글을 작성하려면 로그인해야 합니다.
www.acmicpc.net
https://ahracho.github.io/posts/python/2017-05-09-python-integer-overflow/
[기초 파이썬] 파이썬 3에는 오버플로우가 없다?
오버플로우(Overflow)란? 지난 포스팅에서도 설명하였듯이 C언어에서 변수 혹은 상수의 값은 메모리에 직접 저장이 된다. 예를 들어, 아래와 같이 int 변수 a에 5라는 값을 대입하면, 컴퓨터는 알아
ahracho.github.io
'알고리즘 > 알고리즘 일반' 카테고리의 다른 글
| 문제의 핵심을 이해하고 정확히 구현하는 알고리즘 (0) | 2022.08.09 |
|---|---|
| 코딩테스트를 위한 스택과 큐 기본 이론 (0) | 2022.06.29 |
| 2진수 변환을 가장 빠르게 하는 방법 (0) | 2022.05.19 |
| 사각맵에서 가장 빨리 목적지로 도달하는 최단 경로 찾는 방법 (0) | 2022.05.03 |
| 이차원 배열 회전시키는 방법 (0) | 2022.04.28 |

