1. 문제
주어진 자연수 n을 이진수로 변환할 때 1의 개수와 정확히 같은 1의 개수를 가지는 n보다 작은 자연수의 이진수 변환은 몇개나 있는지 구하는 solution 함수를 작성하면?
2. 제한사항
n은 $2^{30}$이하의 자연수
3. 나의 풀이
처음에는 그냥 format을 이용해 n을 이진수로 변환하고 for문을 이용해 1부터 n보다 작은 자연수까지 모두 이진수로 변환해보면서 1의 개수가 같으면 answer에 1을 더하는 방식으로 구했다
def solution(n):
answer = 0
bin_n_one = format(n,'b').count('1')
for i in range(1,n):
if bin_n_one == format(i,'b').count('1'):
answer += 1
return answer
format(n,'b')를 하면 n을 이진수로 변환한 문자열을 반환하고 여기에 count('1')을 하면 문자열에서 '1'의 개수를 센다
그런데 이제 이렇게 하면 n은 $2^{30}$이하인데 $2^{30}$이면 시간안에 답을 못구한다는게 문제
언제끝날지도 모를정도로 오래걸림

위 그림을 보면 13분 예상할정도
당연하지만 10초안에는 해결해야하는 코딩테스트에서 당연히 오답이겠지
생각을 바꿔서 n이하의 자연수를 모두 검사해보는게 아니라 주어진 n의 이진수가 1이 몇개인지 구하는건 쉬운데
그러면 그 1의 개수만 가지고 이진수를 몇개 만들수있는지 계산해보면 된다
어떻게 할 수 있을까?
예를 들어 $2^{30}$을 2진수로 바꿔보면 1이 1개이고 0이 30개인 길이가 31인데 이것보다 1작은 $2^{30}-1$은 길이가 30인 이진수로 변환된다는 말이지
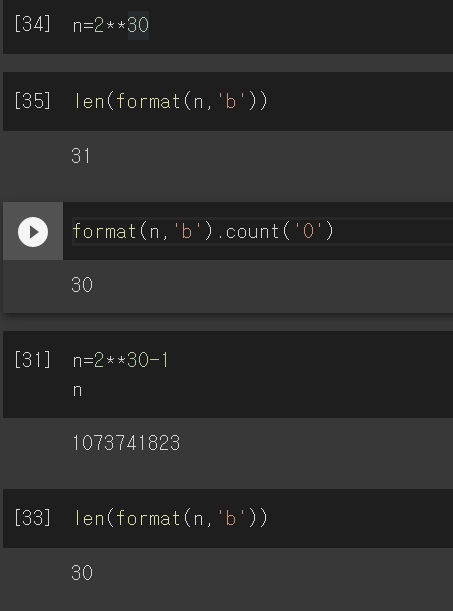
그래서 기본적으로 생각을 하기를 n을 2진수로 바꾸면 1의 개수가 a개이고 0의 개수가 b개이면
1의 개수가 a개이고 0의 개수가 0부터 b-1개까지 전부 검사해서 2진수가 몇개인지 생각을 해보자
그러면 어떻게 가능할까?
1의 개수가 a개이고 0의 개수가 b-3개인 2진수는 몇개일까?
permutations를 이용하면 가능하다고 생각을 했음
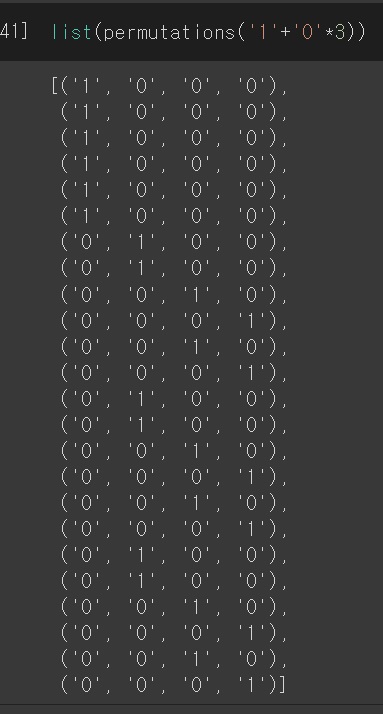
예를 들어 위 그림은 1 1개랑 0 3개를 일렬로 나열해서 만드는 경우의 수인데 보면 중복된게 보인단말이지
set()을 이용해서 중복을 없앨수있다
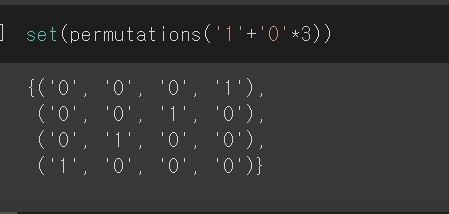
어차피 맨 앞에는 1로 고정을 시켜야하고 나머지를 일렬로 배열하면 된다
예를 들어 n을 2진수로 바꾸면 1이 a개이고 0이 b개라면
1을 맨 앞으로 고정시키고 1을 a-1개, 0을 0~b-1개를 일렬로 배열해서 경우의 수를 구하면 된다
def solution(n):
from itertools import permutations,combinations
answer = 0
bin_n = format(n,'b')
target_one = bin_n.count('1')-1
target_zero = bin_n.count('0')
for num_zero in tqdm(range(target_zero)):
answer += len(set(permutations('1'*target_one+'0'*num_zero)))
return answer
근데 이렇게 하면 역시 오히려 더 느려짐
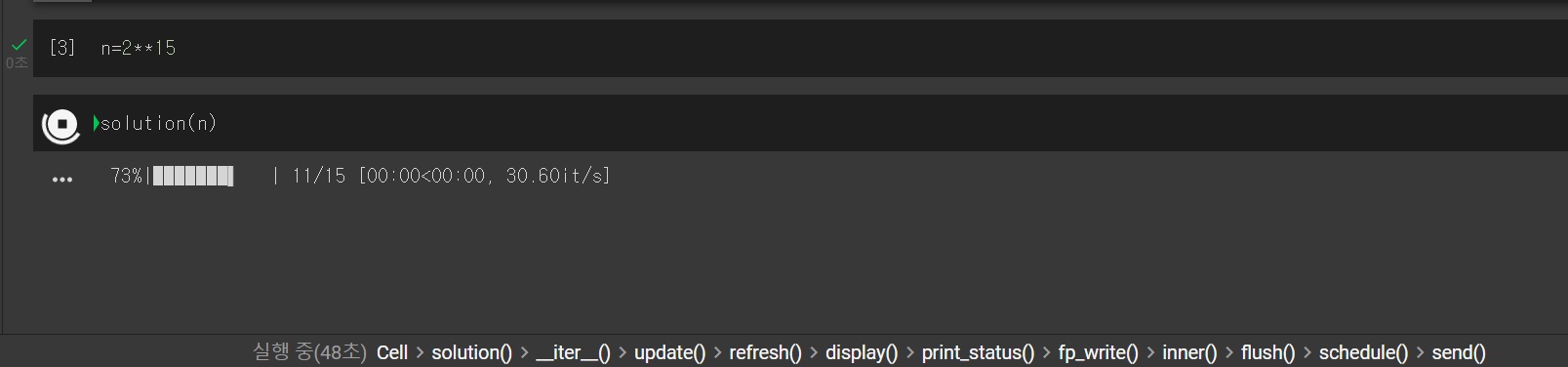
위와 같이 오히려 멈춰버리는
그래서 고민한 끝에 놀라운 방법을 생각했는데
예를 들어서 1이 2개이고 0이 5개인 경우를 생각을 해보면
0을 먼저 7개를 일렬로 나열하면 7개의 자리가 생기는데
그러면 7개의 자리에서 1을 넣을 2개의 자리만 뽑으면 되는거 아닌가?

근데 이러면 맨 앞이 1이 아닌 경우는 제외해야하는 까다로움이 생기니까 역시 1을 맨 앞에 고정을 시키면
결국 1이 1개, 0이 5개인 경우 2진수의 개수를 세면 되니까
0의 자리 6개를 일렬로 나열하고 거기서 1을 넣을 1개의 자리를 선택하면 된다

def solution(n):
from itertools import combinations
answer = 0
bin_n = format(n,'b')
target_one = bin_n.count('1')-1
target_zero = bin_n.count('0')
for num_zero in range(target_zero):
answer += len(list(combinations(range(target_one+num_zero),target_one)))
return answer
format(n,'b')를 이용해서 n을 이진수로 변환하고 여기서 '1'의 개수와 0의 개수를 센다
1은 맨 앞에 고정시킬거니까 target_one = bin_n.count('1') - 1로 할거고
그러면 0의 개수를 0부터 target_zero-1까지 for문을 순회해서
전체 자리 target_one+num_zero만큼 일렬로 나열하고(range(target_one+num_zero))
여기서 1의 개수를 넣을 자리 target_one만큼 뽑는 경우의 수는 combinations로 구할 수 있다
이러면 n이 $2^{30}$이어도 0초만에 계산해줌
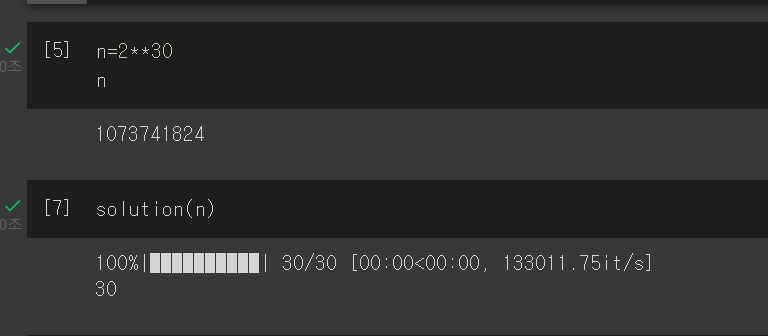
이게 정답인줄 알았는데 실수한 점은 n보다 작은 자연수라면 0의 개수가 무조건 1개이상 작아야한다고 생각한점
사실 n을 2진수로 바꿨을 때 예를 들어
'10000010'이라고 한다면... 이것보다 작은 자연수인데 1의 개수와 0의 개수가 모두 동일한 경우
'10000001'이 존재할 수가 있다는점
그래서 0이 target_zero만큼 존재할때 원래 n보다 작은 자연수가 몇개인지 answer에 더해줘야 정확한 정답일것
근데 그것은 별로 시간이 안걸릴것 같으니까 하나하나 구해보고 실제로 n보다 작은지 검사해볼라고..
그리고 combinations로 구하기엔 오히려 복잡할 것 같아
def solution(n):
from itertools import combinations
answer = 0
bin_n = format(n,'b')
target_one = bin_n.count('1')-1
target_zero = bin_n.count('0')
if target_one >= 1:
a = ['1']+['0']*(target_zero+target_one)
for ind_tuple in list(combinations(range(1,target_one+target_zero+1),target_one)):
b = a.copy()
for ind in ind_tuple:
b[ind] = '1'
if n > int(''.join(b),2):
answer += 1
for num_zero in range(target_zero):
answer += len(list(combinations(range(target_one+num_zero),target_one)))
return answer
target_one=0인 경우는 맨 앞에 1이 있는 '10000', '100000' 등등 이런 경우라서 무조건 이것보다 작은 자연수는
0의 개수가 1개이상 작아진다
그래서 target_one >=1인 경우...
맨 앞은 1로 고정시키고 나머지는 0을 배열하니까 a=['1']+['0']*(target_zero+target_one)으로 해서
a=['1','0','0','0','0','0']
그러면 '0'이 있는 첫번째 인덱스는 1이고 마지막 인덱스는 target_zero+target_one이니까
1번부터 target_zero+target_one까지의 range에서 1을 넣을 자리를 뽑는 combinations를 구하고..
그 combination이 ind_tuple에 들어간다
['1','0','0','0','0','0'] 여기서 1을 1개 넣고싶은데
그러면 ind_tuple은 (1,), (2,), (3,),.... 이렇게 있겠지
다음 a를 copy해서 b로 만들고... ind_tuple의 값들은 1이 들어갈 자리니까...
이제 ind_tuple을 순회해서 ind라 하고 하나씩 b[ind] = '1'로 바꿔준다
예를 들어 ['1','1','0','0','0','0'],.....,['1','0','1','0','0','0'],..... 이런식으로 나오겠지
다음 ''.join(b)로 합치면 '110000',........,'101000',...... 이런식으로 나오는데 int(''.join(b),2)를 하면
''.join(b)가 2진수임을 인식하고 10진수로 바꿔준다
그것을 n과 비교해서 실제로 n보다 작으면 answer에 1을 더해준다

예상한대로 개수차이가 생긴다
4. 되돌아보기
아깝게 실수하긴했는데 상당히 잘 풀었다
컴퓨터 사고방식으로 하나씩 다 세볼 생각에만 빠져가지고 사고가 정지했는데
(1부터 n-1까지 2진수로 바꿔서 1의 개수 비교해보기)
때로는 통계적 방식으로 경우의 수를 세는 방법을 코딩하는것도 효과적인것 같다
(1을 앞에 고정시키고 0을 전부 나열한다음에 1이 들어갈 자리를 뽑는 조합의 수 구하기)
'알고리즘 > 알고리즘 일반' 카테고리의 다른 글
| 코딩테스트를 위한 스택과 큐 기본 이론 (0) | 2022.06.29 |
|---|---|
| 파이썬은 big int는 지원하지만 big float를 지원하지 않는다 (0) | 2022.06.20 |
| 사각맵에서 가장 빨리 목적지로 도달하는 최단 경로 찾는 방법 (0) | 2022.05.03 |
| 이차원 배열 회전시키는 방법 (0) | 2022.04.28 |
| 중복을 허용하는 집합 다루기 (0) | 2022.04.17 |

