1. 결정계수에 대한 오해
결정계수(coefficient of determination) $R^2$은 많은 교재에서나 제곱이라는 그 모습 $R^2$때문에 0이상 1이하라고 오해하기 쉬운데 사실 결정계수는 음수일 수 있다

2. 제곱합
모든 독립변수 x에 대하여 종속변수 y를 가집니다.
가장 적합한 회귀직선을 그려 x의 값에 대하여 y의 값을 예측하고자 합니다.
2-1) 잔차제곱합
y의 예측값을 $\hat{y}$ 이라고 한다면 회귀직선이 예측한 값과 실제 y값의 차이를 이용해 error를 계산할 수 있습니다.
이러한 차이 error를 제곱하여 더한 것을 잔차제곱합이라 부르고 보통 SSE라고 표현합니다.
$$SSE = \sum (y-\hat{y})^2$$
2-2) 전체제곱합
다음으로 실제 y의 평균값을 계산할 수 있습니다. 이것을 $\bar{y}$라고 씁니다.
우리가 $\bar{y}$를 그린다면 상수이기 때문에 데이터를 통과하는 수평선으로 그려집니다.
실제 y값으로부터 수평선과의 차이를 제곱하고 더한다면 전체제곱합이라고 부르고 SST라고 보통 씁니다.
$$ SST=\sum _{} ^{} (y- \bar{y} ) ^{2}$$
2-3) 회귀제곱합
예측값 $\hat{y}$ 과 평균값 $\bar{y}$ 의 차이를 제곱하고 더할 수 있습니다. 이것을 회귀제곱합이라고 부르고 SSR이라고 씁니다.
$$SSR=\sum _{} ^{} ( \hat{y} - \bar{y} ) ^{2}$$
3. 결정계수의 정의
주어진 데이터를 설명하는 가장 단순한 선형 모형은 데이터의 mean value인 $\bar{y}$ 로 전체 데이터를 설명하는 것입니다.
그럴 경우 모든 데이터의 예측값은 $\hat{y} = \bar{y}$ 이므로
전체제곱합 $SST=\sum _{} ^{} (y- \bar{y} ) ^{2}$ 와 잔차제곱합 $SSE = \sum (y-\hat{y})^2$는 동일하여 SST = SSE가 됩니다.
따라서 기준이 되는 모형의 $\frac{SSE}{SST} = 1$이 됩니다.
결정계수란 내가 적합시킨 선형모형이 이런 mean value 모형보다 얼마나 데이터의 분산을 잘 설명하느냐로 계산됩니다.
이를 수학적으로 표현하면
$$R^2 = 1 - \frac{SSE}{SST}$$
로 구해집니다.
전항인 1은 mean value모형의 $\frac{SSE}{SST}$이고 후항은 적합시킨 선형모형의 $\frac{SSE}{SST}$가 됩니다.
그래서 기준모형인 $y=\bar{y}$와 적합시킨 선형모형 $y=\hat{\alpha}+\hat{\beta}x+\varepsilon$의 $\frac{SSE}{SST}$를 비교하여 얼마나 잘 설명하는지를 수학적으로 나타냅니다.
4. 제곱합의 분해
전체제곱합 $ SST=\sum _{} ^{} (y- \bar{y} ) ^{2}$에서 $(y- \bar{y} ) ^{2}$안에 $\hat{y}$을 더하고 빼면
$$ SST=\sum _{} ^{} (y- \hat{y}+ \hat{y}+ \bar{y} ) ^{2}$$
를 얻습니다.
이 식을 정리하면 다음과 같습니다.
$$SST=\sum _{} ^{} (y- \hat{y} ) ^{2} + \sum _{} ^{} ( \hat{y} - \bar{y} ) ^{2} +2 \sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )$$
그런데 여기서 많은 경우 오해하는 부분은
$$ \sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )=0 $$
이 항상 성립하여
$$SST=\sum _{} ^{} (y- \hat{y} ) ^{2} + \sum _{} ^{} ( \hat{y} - \bar{y} ) ^{2} =SSE+SSR$$
로 분해된다는 점이다.
그런데 사실
$$\sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )=0$$이 항상 성립하지는 않는다. 왜 그런지 생각해보자.
4-1) 절편이 있는 회귀분석
일반적으로 절편이 있는 회귀모형
$$y= \alpha + \beta x+ \epsilon $$에 대하여 최소제곱법에 의해 회귀계수를 추정하면 다음과 같다.
$$\hat{\alpha } = \bar{y} - \hat{\beta } \bar{x}$$
$$\hat{\beta } = \frac{\sum _{} ^{} (x- \bar{x} )(y- \bar{y} )}{\sum _{} ^{} (x- \bar{x} ) ^{2}}$$
잔차(residual) $y- \hat{y} =e$라고 표현하고, $\hat{y} = \hat{\alpha } + \hat{\beta } x$이므로 $\sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )$에 $\hat{\alpha } = \bar{y} - \hat{\beta } \bar{x}$을 대입하면 다음과 같다.
$$\sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )= \sum _{} ^{} e( \hat{\alpha } + \hat{\beta } x-( \hat{\alpha } + \hat{\beta } \bar{x} ))= \hat{\beta } \sum _{} ^{} e(x- \bar{x} )$$
정규방정식(normal equation) $\sum _{} ^{} e=0$ , $\sum _{} ^{} ex=0$을 이용하면
$$\hat{\beta } \sum _{} ^{} ex- \hat{\beta } \bar{x} \sum _{} ^{} e=0$$
그러므로 절편이 있는 선형회귀분석 $y= \alpha + \beta x+ \epsilon $에서는 $\sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )=0$이 성립하여
$$SST=\sum _{} ^{} (y- \hat{y} ) ^{2} + \sum _{} ^{} ( \hat{y} - \bar{y} ) ^{2} =SSE+SSR$$이 항상 성립한다
4-2) 절편이 없는 회귀분석
이번엔 절편이 없는 회귀분석 $y= \beta x+ \epsilon $을 가정하면
먼저 정규방정식(normal equation)은 오차제곱합 $\sum _{} ^{} (y- \beta x) ^{2} =0$을 $\beta$ 로 미분하여 $-2 \sum _{} ^{} (y- \beta x)x=0$으로부터
$$\sum _{} ^{} (y- \hat{\beta } x)x= \sum _{} ^{} ex=0$$을 얻는다.
그러므로
$$\sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )= \sum _{} ^{} e( \hat{\beta } x- \bar{y} )= \hat{\beta } \sum _{} ^{} ex- \bar{y} \sum _{} ^{} e=- \bar{y} \sum _{} ^{} e$$
이다.
4-3) 차이점
가장 중요한 차이점은 잔차의 합
$$\sum _{} ^{} e=0$$
이라는 보장이 없다
그래서 절편이 없는 회귀모형에서는
$$SST=\sum _{} ^{} (y- \hat{y} ) ^{2} + \sum _{} ^{} ( \hat{y} - \bar{y} ) ^{2} =SSE+SSR$$이 반드시 성립하지는 않는다.
물론 절편이 없더라도 잔차의 합 $\sum _{} ^{} e=0$이 된다면 성립할 수 있다.
5. 결정계수는 언제 음수가 될 수 있는가
따라서 결정계수의 정의
$$R ^{2} =1- \frac{SSE}{SST}$$로부터
절편이 있는 회귀모형이라면 반드시 $SST=SSE+SSR$이므로 많은 사람들이 알던 공식으로
$$R ^{2} =1- \frac{SSE}{SST} = \frac{SSR}{SST}$$ 바꿀 수 있다.
이 때 $$R ^{2} = \frac{SSR}{SST} = \frac{\sum _{} ^{} ( \hat{y} - \bar{y} ) ^{2}}{\sum _{} ^{} (y- \bar{y} ) ^{2}}$$
이므로 $$0 \leq R ^{2} \leq 1$$
이 성립한다.
그러나 절편이 없는 회귀모형이라면
$$SST=SSE+SSR+2 \sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )$$이므로 전체를 $SST$로 나눈다면
$$1=\frac{SSE}{SST} + \frac{SSR}{SST} + \frac{2 \sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )}{SST}$$에서
$$1-\frac{SSE}{SST}=\frac{SSR}{SST} + \frac{2 \sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )}{SST}$$이므로
$$R ^{2} = \frac{SSR}{SST} + \frac{2 \sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )}{SST}$$을 얻는다.
그러므로
$$2 \sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )<0$$이면 결정계수는 음수를 가질 수 있다.
6. 예를 들어서 생각해보기
결정계수는 앞에서 설명한 것처럼 mean value 모형 $y=\hat{y}$보다 적합시킨 회귀모형이 얼마나 데이터를 잘 설명하느냐를 나타낸다.
특히 $$2 \sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )<0$$이면 결정계수 $R^2$이 음수를 가질 수 있다.
그 말은
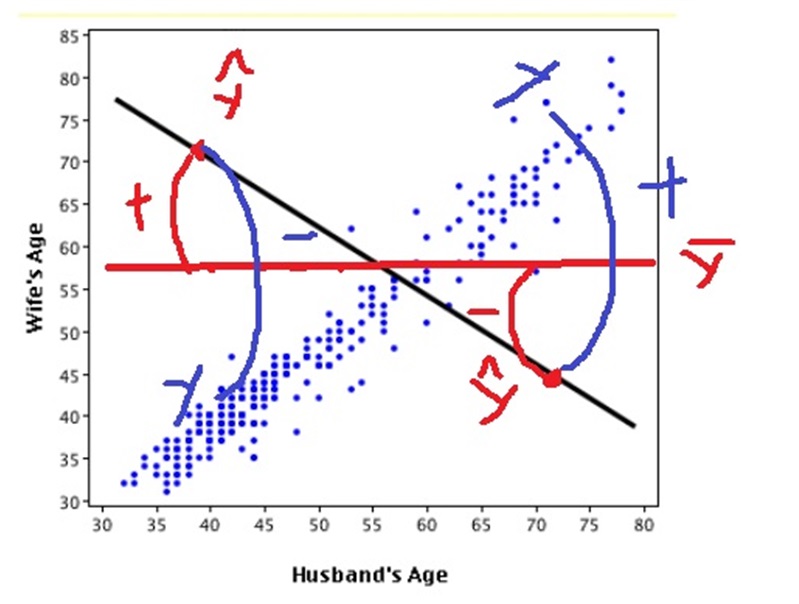
$$(y- \hat{y} )<0, ( \hat{y} - \bar{y} )>0$$이거나 $$(y- \hat{y} )>0,( \hat{y} - \bar{y} )<0$$
이면 결정계수 $R^2$이 음수를 가진다는 뜻이다.
7. 핵심요약
1) 결정계수는 $R ^{2} = \frac{SSR}{SST} =1- \frac{SSE}{SST}$가 아니라 $R ^{2} =1- \frac{SSE}{SST}$이다.
이 식은 가장 단순한 모형 mean value $y= \bar{y}$보다 적합시킨 모형 $y= \alpha + \beta x+ \epsilon$ 이 데이터를 얼마나 잘 설명하느냐를 나타낸다.
2) 제곱합을 분해하면 $SST=SSE+SSR$이 아니라 $SST=\sum _{} ^{} (y- \hat{y} ) ^{2} + \sum _{} ^{} ( \hat{y} - \bar{y} ) ^{2} +2 \sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )$이다.
SST로 나누면 $R ^{2} = \frac{SSR+2 \sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )}{SST}$이다.
3) 절편이 있는 회귀모형 $y= \alpha + \beta x+ \epsilon$을 가정한다면 $2 \sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )=0$이 성립하지만 절편이 없는 회귀모형 $y= \beta x+ \epsilon$을 가정한다면
$2 \sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )=0$이 반드시 성립하지 않는다
왜냐하면 절편이 없는 회귀모형의 경우 잔차의 합 $\sum _{} ^{} e=0$이 수학적으로 보장되지 않는다.
4) 그래서 결정계수 $R ^{2} = \frac{SSR+2 \sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )}{SST}$는 음수일 수 있다.
적합시킨 모형이 mean value보다 설명을 못해서 $2 \sum _{} ^{} (y- \hat{y} )( \hat{y} - \bar{y} )<0$이면 $R ^{2} <0$일 수 있다.
5) 일반적으로 단순선형회귀분석에서 설명변수와 종속변수의 상관계수의 제곱이 결정계수와 같다고 알려져있는데 역시 절편이 있어야만 성립한다.
8. 참조
https://stats.stackexchange.com/questions/183265/what-does-negative-r-squared-mean
What does negative R-squared mean?
Let's say I have some data, and then I fit the data with a model (a non-linear regression). Then I calculate the R-squared ($R^2$). When R-squared is negative, what does that mean? Does that mean my
stats.stackexchange.com
https://en.wikipedia.org/wiki/Coefficient_of_determination
Coefficient of determination - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Indicator for how well data points fit a line or curve Ordinary least squares regression of Okun's law. Since the regression line does not miss any of the points by very much, the R2 o
en.wikipedia.org
'다시보는 통계학' 카테고리의 다른 글
| 분포함수에 관한 중요한 정리(theorem) (0) | 2021.12.07 |
|---|---|
| 누적확률분포함수(cumulative probability distribution)에 대하여 (0) | 2021.12.06 |
| 확률(probability)과 가능도(likelihood)는 어떻게 다를까? (0) | 2021.11.18 |
| p-value에 대한 오해 (0) | 2021.10.06 |
| 머신러닝 모델에서의 bias와 variance에 대하여 (0) | 2021.10.06 |

