개요
- 현대 신경망에서 정규화(Normalization) 계층은 필수적인 요소로 여겨짐.
- 본 연구에서는 정규화 없이도 동일하거나 더 나은 성능을 내는 방법을 제시.
- Dynamic Tanh (DyT)라는 간단한 연산을 도입하여 정규화 계층을 대체함.
- DyT는 DyT(x) = tanh(αx)의 형태를 가지며, 입력값을 조정하고 극단값을 억제하는 역할 수행.
주요 기여
- 정규화 계층이 없어도 학습 가능
- Layer Normalization (LN) 없이도 Transformer 모델이 안정적으로 학습됨을 실험적으로 입증.
- DyT는 tanh 형태의 S-커브를 활용하여 정규화 계층의 효과를 모방.
- 다양한 영역에서 검증
- 시각 인식, 언어 모델링, 음성 인식 등 다양한 태스크에서 DyT 적용.
- ViT, ConvNeXt, LLaMA 등의 최신 모델에 적용하여 LN 대비 유사하거나 더 나은 성능 달성.
- 성능 및 속도 향상
- DyT 적용 시 학습 및 추론 속도가 향상됨.
- LLaMA 모델에서 DyT는 기존 RMSNorm보다 훈련 속도를 8% 개선.
실험 결과
- 이미지 분류 (ImageNet-1K): DyT를 적용한 ViT 및 ConvNeXt 모델이 LN 대비 동등 또는 향상된 성능을 보임.
- 자기 지도 학습 (Self-Supervised Learning): MAE, DINO 등의 자기 지도 학습에서도 LN과 동등한 성능을 유지.
- 대규모 언어 모델 (LLM): LLaMA 7B~70B 모델에서 RMSNorm을 대체하여 학습 가능하며, 성능 차이 없음.
- 추론 및 학습 속도: DyT 적용 시 LLaMA 모델의 학습 및 추론 속도가 8% 향상.
분석 및 한계점
- DyT는 LN과 RMSNorm을 대체하는 데 효과적이지만, BatchNorm(BN)을 대체하는 데는 어려움이 있음.
- LLM에서는 α 초기값 조정이 중요하며, 모델 크기에 따라 최적의 α값이 달라짐.
- 기존 LN과 RMSNorm 기반 네트워크를 변경 없이 적용 가능하지만, BN을 사용하는 네트워크에서는 추가 연구 필요.
결론
- DyT는 정규화 계층을 제거하면서도 성능을 유지하는 새로운 방법으로, 신경망의 효율성과 속도를 개선할 가능성이 있음.
- 향후 연구에서는 BN을 포함한 다른 정규화 방법을 대체할 가능성을 탐색할 필요가 있음.
----------------------------------------------------------------------------------------------------------------------------------------------------------
1. 개요
지난 10년 동안 정규화(Normalization) 계층은 현대 신경망에서 가장 기본적인 구성 요소 중 하나로 자리 잡았다.
이는 2015년 Ioffe와 Szegedy가 배치 정규화(Batch Normalization)를 발명한 것에서 시작되었으며, 이를 통해 시각적 인식 모델의 수렴 속도가 크게 향상되고 성능이 개선되면서 빠르게 확산되었다.
이후 다양한 네트워크 아키텍처와 도메인에 맞춰 여러 정규화 기법들이 제안되었으며(Ba et al., 2016; Ulyanov et al., 2016; Wu and He, 2018; Zhang and Sennrich, 2019), 현재 대부분의 현대 신경망은 정규화 계층을 사용하고 있다.
특히, Transformer 아키텍처에서 가장 널리 사용되는 정규화 방식은 레이어 정규화(Layer Normalization, LN)이다(Ba et al., 2016; Vaswani et al., 2017; Dosovitskiy et al., 2020).
정규화 계층이 널리 채택된 이유는 주로 최적화 과정에서의 경험적 이점 때문이다(Santurkar et al., 2018; Bjorck et al., 2018).
정규화 계층은 학습 속도를 높이고, 안정적인 수렴을 유도하며, 신경망이 점점 더 넓고 깊어질수록 이러한 필요성은 더욱 커진다(Brock et al., 2021a; Huang et al., 2023).
따라서, 정규화 계층은 딥러닝 모델을 효과적으로 학습하는 데 필수적인 요소로 여겨져 왔다.
최근 몇 년 동안 새로운 아키텍처들은 주로 어텐션(Attention)이나 합성곱(Convolution) 계층을 대체하는 방식으로 발전했지만(Tolstikhin et al., 2021; Gu and Dao, 2023; Sun et al., 2024; Feng et al., 2024), 정규화 계층은 거의 항상 유지되는 특징이 있다.
본 논문에서는 이러한 기존의 믿음에 도전하며, Transformer에서 정규화 계층을 대체할 수 있는 간단한 방법을 제안한다.
우리는 LN 계층이 입력을 tanh 형태의 S자 곡선으로 변환하여, 입력 활성값을 조정하고 극단적인 값을 억제한다는 점에 주목했다.
이를 바탕으로, **Dynamic Tanh (DyT)**라는 새로운 요소별(element-wise) 연산을 제안한다.
DyT는 다음과 같이 정의된다:
$$ DyT(x) = tanh(\alpha x) $$
여기서 α는 학습 가능한 파라미터로, LN과 유사한 역할을 수행하면서도 활성 통계를 계산할 필요 없이 동일한 효과를 제공한다.
DyT를 적용하는 방법은 매우 간단하다.
기존 정규화 계층을 DyT로 직접 대체하면 된다(그림 1 참고).
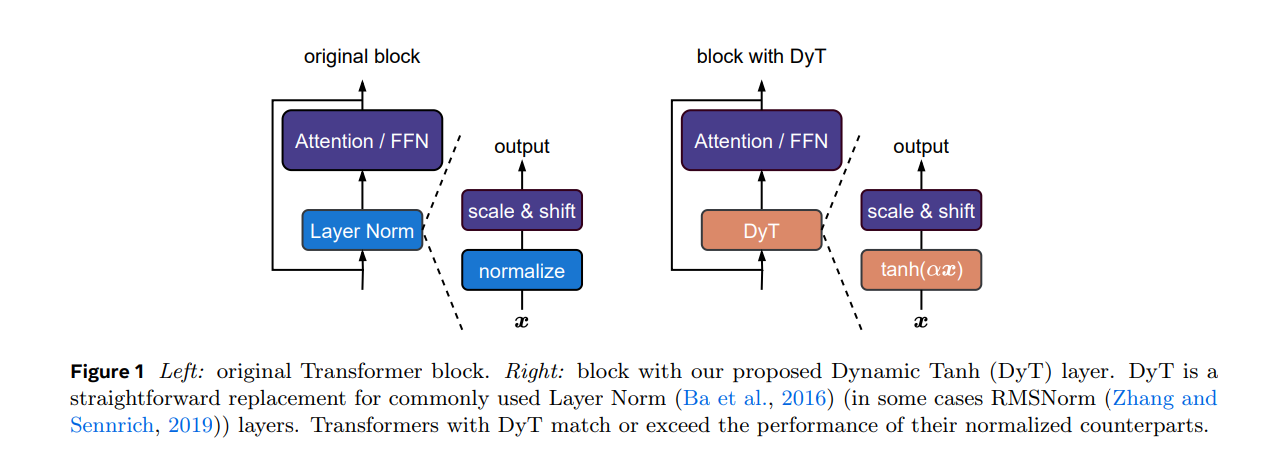
우리는 DyT를 시각 및 언어 Transformer 모델에 적용하여 학습이 안정적으로 진행되며, 최종 성능이 높은 수준으로 유지됨을 실험적으로 증명했다.
또한, DyT는 기존 아키텍처에서 학습 하이퍼파라미터를 거의 변경할 필요가 없으며, 정규화 계층이 필수적이라는 기존의 통념을 뒤집는다.
더욱이, 초기 실험 결과에 따르면 DyT는 학습 속도와 추론 속도를 개선할 가능성이 있어, 효율성을 중시하는 신경망 설계에서 유망한 대안이 될 수 있음을 시사한다.
2. 정규화 계층
우리는 먼저 정규화(Normalization) 계층에 대해 개괄적으로 살펴본다.
대부분의 정규화 계층은 공통적인 수식을 따른다.
입력 x가 (B, T, C) 형태일 때, 여기서 B는 배치 크기(Batch size), T는 토큰 개수(Number of tokens), C는 각 토큰의 임베딩 차원(Embedding dimension per token)을 의미한다.
일반적으로 정규화된 출력은 다음과 같이 계산된다:
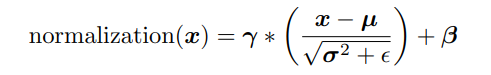
여기서 $\epsilon$는 매우 작은 상수이며, $\gamma$와 $\beta$는 (C,) 형태의 학습 가능한 벡터 파라미터이다.
이들은 각각 스케일링(Scaling) 및 **시프팅(Shifting)**을 담당하는 선형 변환 계수로, 정규화된 출력 값을 원하는 범위로 조정할 수 있도록 한다.
$\mu$와 $\sigma^2$는 각각 입력의 평균(Mean)과 분산(Variance)을 나타낸다.
정규화 방법들은 주로 이 두 통계값을 계산하는 방식에서 차이가 있다.
이로 인해 $\mu$와 $\sigma^2$의 차원이 달라지며, 계산 과정에서 브로드캐스팅(Broadcasting)이 적용된다.
배치 정규화(Batch Normalization, BN)
배치 정규화(BN)는 2015년 Ioffe와 Szegedy가 제안한 최초의 현대적인 정규화 계층이다.
주로 합성곱 신경망(ConvNet) 모델에서 널리 사용되었다(Szegedy et al., 2016; He et al., 2016; Xie et al., 2017).
BN의 도입은 딥러닝 아키텍처 설계에서 중요한 이정표로 간주된다.
BN은 배치 전체(Batch)와 토큰 차원(Tokens)에 걸쳐 평균과 분산을 계산하며, 다음과 같이 정의된다:
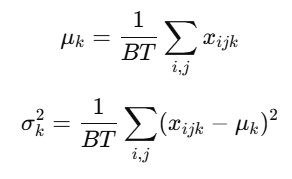
다른 정규화 기법
BN 외에도 그룹 정규화(Group Normalization, GN)(Wu and He, 2018) 및 인스턴스 정규화(Instance Normalization, IN)(Ulyanov et al., 2016)와 같은 정규화 방법들이 있다.
이들은 초기에는 객체 탐지(Object Detection) 및 **이미지 스타일 변환(Image Stylization)**과 같은 특정 작업을 위해 제안되었으며, 기본적인 계산 방식은 BN과 유사하지만 **통계를 계산하는 축(Axis)과 범위(Range)**에서 차이가 있다.
레이어 정규화(LN) 및 RMS 정규화(RMSNorm)
레이어 정규화(Layer Normalization, LN) (Ba et al., 2016)와 루트 평균 제곱 정규화(Root Mean Square Normalization, RMSNorm) (Zhang and Sennrich, 2019)은 Transformer 아키텍처에서 주로 사용되는 두 가지 정규화 기법이다.
LN은 각 샘플의 각 토큰별로 통계를 독립적으로 계산하며, 다음과 같이 정의된다:
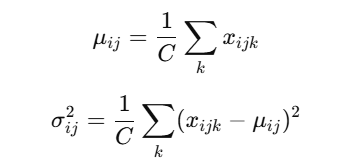
한편, RMSNorm (Zhang and Sennrich, 2019)은 LN에서 평균을 빼는(mean-centering) 단계를 제거하고, 다음과 같이 입력을 정규화하는 방식으로 단순화되었다:

오늘날 대부분의 최신 신경망에서는 LN이 간단하면서도 범용적으로 사용될 수 있기 때문에 LN이 주로 사용된다.
하지만 최근에는 RMSNorm이 특히 대규모 언어 모델(LLM)에서 인기를 얻고 있으며, 다음과 같은 모델에서 사용되고 있다:
- T5 (Raffel et al., 2020)
- LLaMA (Touvron et al., 2023a,b; Dubey et al., 2024)
- Mistral (Jiang et al., 2023)
- Qwen (Bai et al., 2023; Yang et al., 2024)
- InternLM (Zhang et al., 2024; Cai et al., 2024)
- DeepSeek (Liu et al., 2024; Guo et al., 2025)
본 연구에서 다루는 대부분의 Transformer 모델은 LN을 사용하지만, LLaMA 모델은 RMSNorm을 채택하고 있다.
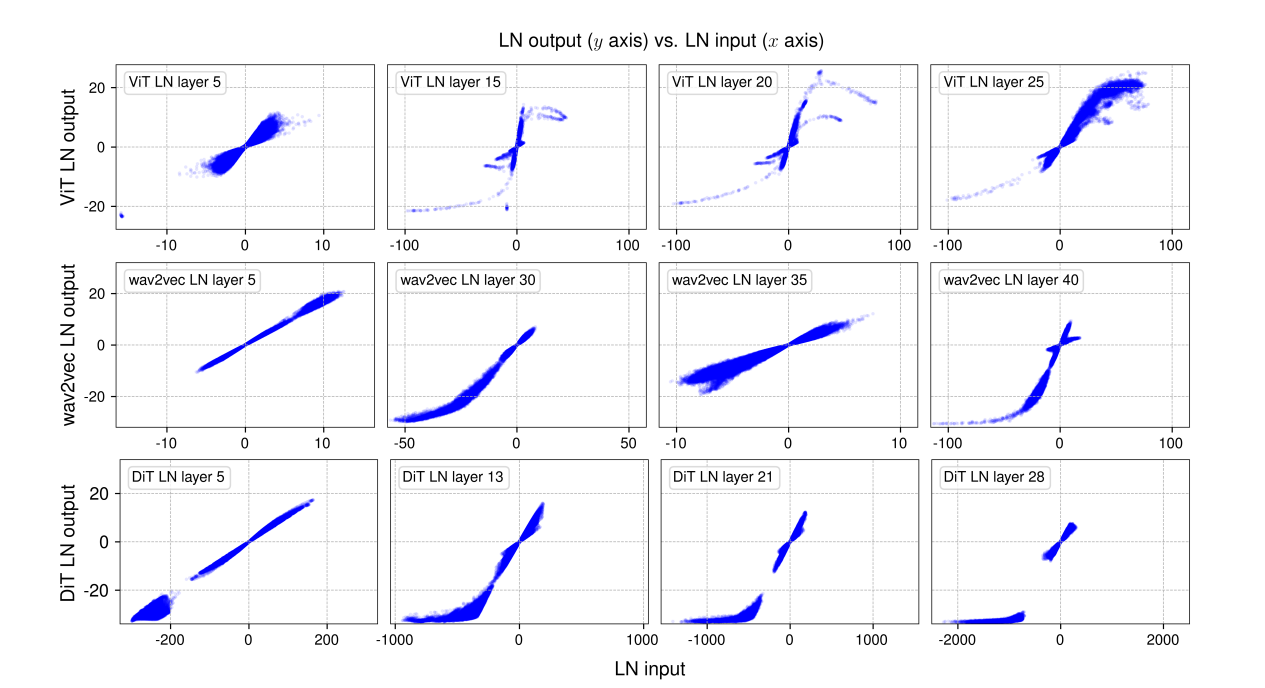
우리는 미니배치(mini-batch) 샘플을 추출하여 각 모델에서 네 개의 LN 계층의 입력/출력 값을 시각화하였다.
여기서 출력 값은 LN의 선형 변환(Affine Transformation) 이전의 값을 의미한다.
결과적으로, S자(S-shaped) 곡선이 tanh 함수와 매우 유사한 형태를 나타냄을 확인할 수 있었다(그림 3 참고).
또한, 초기 계층의 출력 값은 보다 선형적인 형태를 보이지만, 이는 tanh 함수의 중심 부분과 일치하는 특성을 가진다.
이러한 관찰을 바탕으로, 우리는 입력 스케일 차이를 조정할 수 있는 학습 가능한 스케일링 계수 α를 갖는 Dynamic Tanh (DyT) 연산을 제안하게 되었다.
DyT는 LN을 대체할 수 있는 새로운 방식으로 활용될 수 있다.
Normalization Layers는 무엇을 하나요?
우리는 훈련된 네트워크에서 정규화 계층의 동작을 경험적으로 연구합니다.
이 분석을 위해, 우리는 ImageNet-1K(2009)의 Vision Transformer 모델(ViT-B)(Dosovitskiy et al., 2020), LibriSpeech(Panayotov et al., 2015)에서 훈련된 wav2vec 2.0 Large Transformer 모델(Baevski et al., 2020), 그리고 ImageNet-1K에서 훈련된 Diffusion Transformer(DiT-XL)(Peebles and Xie, 2023)을 사용합니다.
모든 경우에서 LN(Layer Normalization)은 모든 Transformer 블록과 마지막 선형 프로젝션 전에 적용됩니다.
이 세 가지 훈련된 네트워크에 대해, 우리는 샘플 미니배치를 샘플링하고 네트워크를 통해 순방향 패스를 진행합니다.
그런 다음, 우리는 정규화 계층의 입력과 출력을 측정합니다.
즉, 정규화 작업 직전에 해당하는 텐서와 학습 가능한 어파인 변환 전에 해당하는 텐서를 측정합니다.
LN은 입력 텐서의 차원을 유지하기 때문에, 입력과 출력 텐서 요소 간에 일대일 대응 관계를 설정할 수 있어 이들의 관계를 직접 시각화할 수 있습니다.
세 모델 모두에서, 초기 LN 계층(그림 2의 첫 번째 열)에서는 입력과 출력 간의 관계가 대부분 선형적이며, x-y 플롯에서 직선처럼 나타납니다.
그러나 더 깊은 LN 계층에서는 더 흥미로운 관찰을 할 수 있습니다.
이 더 깊은 계층에서 두드러진 관찰은 대부분의 곡선 형태가 tanh 함수로 표현된 전체 또는 부분적인 S자 형태와 매우 유사하다는 것입니다(그림 3 참조).

LN 계층이 입력 텐서를 선형적으로 변환할 것이라고 예상할 수 있는데, 평균을 빼고 표준 편차로 나누는 것은 선형 연산이기 때문입니다.
LN은 토큰별로 정규화되어, 각 토큰의 활성화만 선형적으로 변환합니다.
그러나 토큰마다 평균과 표준 편차 값이 다르기 때문에, 모든 입력 텐서의 활성화에 대해 선형성이 모두 유지되지 않습니다.
그럼에도 불구하고 실제 비선형 변환이 스케일링된 tanh 함수와 매우 유사하다는 점은 여전히 놀라운 일입니다.
S자 곡선에 대해, 우리는 x 값이 0에 가까운 지점으로 표시되는 중앙 부분이 여전히 주로 선형적인 형태임을 주목합니다.
대부분의 점들(약 99%)은 이 선형 범위에 속합니다.
그러나 여전히 이 범위를 벗어나는 점들이 많으며, 이들은 "극단적" 값으로 간주됩니다.
예를 들어, ViT 모델에서는 x 값이 50보다 크거나 -50보다 작은 경우입니다.
정규화 계층이 이러한 값들에 대해 주는 주요 효과는 이를 덜 극단적인 값으로 압축하여 대부분의 점들과 더 일치시키는 것입니다.
이는 정규화 계층이 단순한 어파인 변환 계층으로 근사될 수 없는 부분입니다.
우리는 이러한 비선형적이고 불균형적인 압축 효과가 정규화 계층을 중요하고 필수적으로 만든다고 가설을 제시합니다.
Ni et al. (2024)의 최근 연구에서도 LN 계층이 도입하는 강력한 비선형성에 대해 강조하며, 이 비선형성이 모델의 표현 능력을 어떻게 향상시키는지를 보여줍니다.
더욱이, 이 압축 행동은 큰 입력에 대한 생물학적 뉴런의 포화 특성과 유사하며, 이는 약 1세기 전에 처음으로 관찰된 현상입니다(Adrian, 1926; Adrian and Zotterman, 1926a,b).
LN 계층이 각 토큰에 대해 선형 변환을 수행하면서도 극단적인 값을 비선형적으로 압축하는 방식은 어떻게 되는 것일까요?
이를 이해하기 위해, 우리는 토큰과 채널로 그룹화된 점들을 시각화합니다.
이는 그림 2에서 ViT에 대한 두 번째와 세 번째 서브플롯을 사용하여 시각화하며, 더 명확하게 하기 위해 샘플링된 점들의 하위 집합을 사용합니다.
우리가 플로팅할 채널을 선택할 때, 극단적인 값을 가진 채널도 포함시키는 것을 확인합니다.

그림 4의 왼쪽 두 패널에서는 각 토큰의 활성화를 같은 색으로 시각화합니다.
우리는 모든 토큰에서 나온 점들이 직선을 형성하는 것을 관찰합니다.
그러나 각 토큰은 다른 분산을 가지기 때문에 기울기가 다릅니다.
입력 x 범위가 작은 토큰은 분산이 작은 경향이 있으며, 정규화 계층은 그들의 활성화를 더 작은 표준 편차로 나누므로 직선에서 더 큰 기울기를 생성합니다.
이들이 모여 S자 형태를 이루며, 이는 tanh 함수와 유사합니다.
오른쪽 두 패널에서는 각 채널의 활성화를 같은 색으로 시각화합니다.
우리는 다른 채널들이 극단적인 값의 입력 범위를 크게 다르게 가지는 경향이 있음을 알게 되며, 몇몇 채널(예: 빨간색, 초록색, 분홍색)은 큰 극단적 값을 보입니다.
이 채널들이 정규화 계층에 의해 가장 많이 압축됩니다.
동적 Tanh (DyT)
정규화 계층의 형태와 스케일링된 tanh 함수의 유사성에서 영감을 받아, 우리는 정규화 계층을 대체할 수 있는 동적 Tanh(DyT)를 제안합니다.
입력 텐서 x가 주어지면, DyT 계층은 다음과 같이 정의됩니다:
$$ DyT(x) = γ ∗ tanh(αx) + β $$
여기서 α는 입력의 범위에 따라 다르게 스케일링할 수 있도록 하는 학습 가능한 스칼라 매개변수로, x의 스케일 차이를 반영합니다(그림 2 참조).
그래서 우리는 이 전체 연산을 "동적" Tanh라고 명명합니다.
γ와 β는 학습 가능한 채널별 벡터 매개변수로, 모든 정규화 계층에서 사용하는 것과 동일합니다.
이들은 출력이 원래의 스케일로 다시 스케일링되도록 합니다.
이는 때때로 별도의 어파인 계층으로 간주되기도 하지만, 우리의 목적에서는 이를 DyT 계층의 일부로 간주하며, 정규화 계층이 이를 포함하는 방식과 동일합니다.
DyT의 Pytorch와 유사한 의사코드 구현은 알고리즘 1을 참조하십시오.

DyT 계층을 기존 아키텍처에 통합하는 것은 간단합니다
하나의 DyT 계층이 하나의 정규화 계층을 대체합니다(그림 1 참조).
이는 어텐션 블록, FFN 블록, 최종 정규화 계층 내의 정규화 계층에 적용됩니다.
DyT는 활성화 함수처럼 보이거나 활성화 함수로 간주될 수 있지만, 본 연구에서는 DyT를 원래 아키텍처의 활성화 함수(GELU 또는 ReLU 등)를 변경하지 않고 정규화 계층만 대체하는 데 사용합니다.
네트워크의 다른 부분들도 그대로 유지됩니다.
또한 DyT가 잘 작동하기 위해 원래 아키텍처에서 사용된 하이퍼파라미터를 조정할 필요가 거의 없다는 점을 관찰합니다.
우리는 항상 γ를 모두 1로 초기화하고, β를 모두 0으로 초기화하여 정규화 계층을 따릅니다.
스케일러 파라미터 α의 경우, 기본 초기값인 0.5가 일반적으로 충분하며, LLM 훈련을 제외한 대부분의 경우에 적용됩니다.
α 초기화에 대한 자세한 분석은 7장에서 제공됩니다. 특별히 명시되지 않는 한, 우리의 후속 실험에서는 α를 0.5로 초기화합니다.
DyT는 새로운 유형의 정규화 계층이 아닙니다.
왜냐하면 그것은 통계나 다른 종류의 집계를 계산하지 않고, 포워드 패스 동안 텐서의 각 입력 요소에 대해 독립적으로 작동하기 때문입니다.
그러나 DyT는 정규화 계층의 효과를 보존하면서 극단적인 값을 비선형적으로 압축하고, 입력의 매우 중심 부분을 거의 선형적으로 변환하는 특성을 가집니다.
우리는 Vision Transformer (ViT) (Dosovitskiy et al., 2020)와 ConvNeXt (Liu et al., 2022)의 "Base"와 "Large" 크기를 ImageNet-1K 분류 작업(Deng et al., 2009)에서 훈련했습니다.
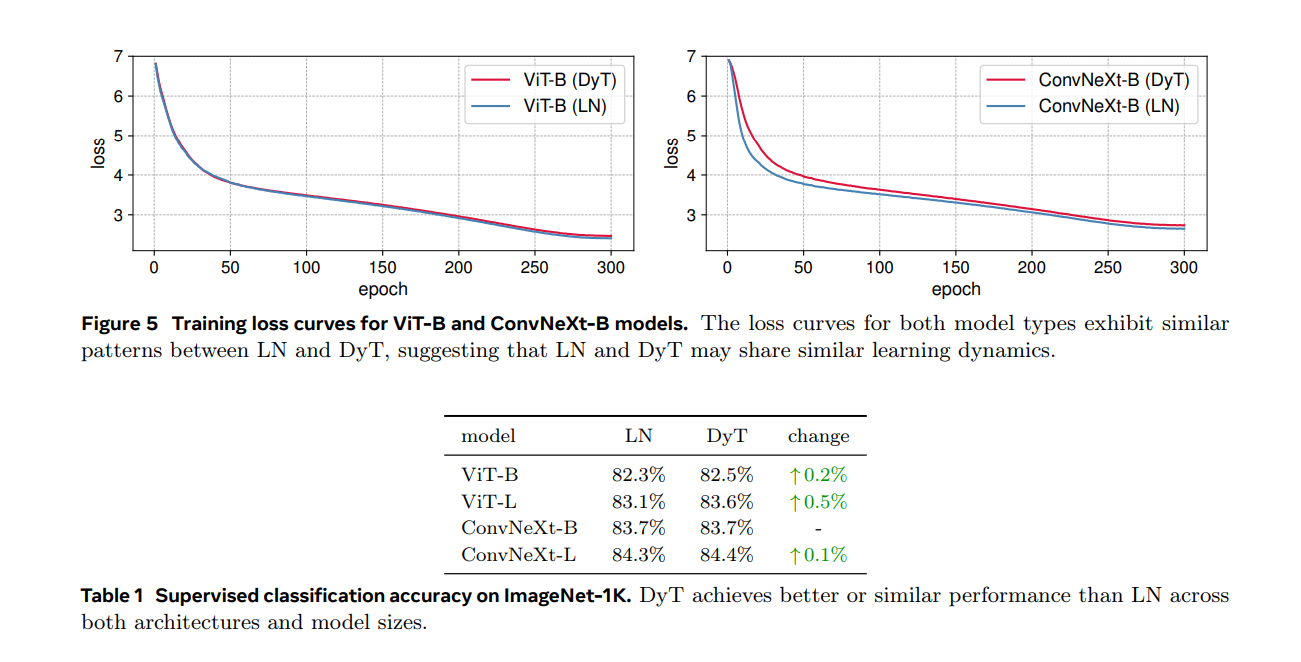
이 모델들은 인기 있고 distinct한 연산을 수행하기 때문에 선택되었습니다: ViT에서의 어텐션과 ConvNeXt에서의 합성곱. 표 1은 top-1 분류 정확도를 보고합니다.
DyT는 두 아키텍처와 모델 크기에서 LN보다 약간 더 우수한 성능을 보였습니다.
우리는 또한 ViT-B와 ConvNeXt-B의 훈련 손실을 그림 5에 나타냈습니다.
이 곡선은 DyT와 LN 기반 모델의 수렴 행동이 매우 일치함을 보여줍니다.
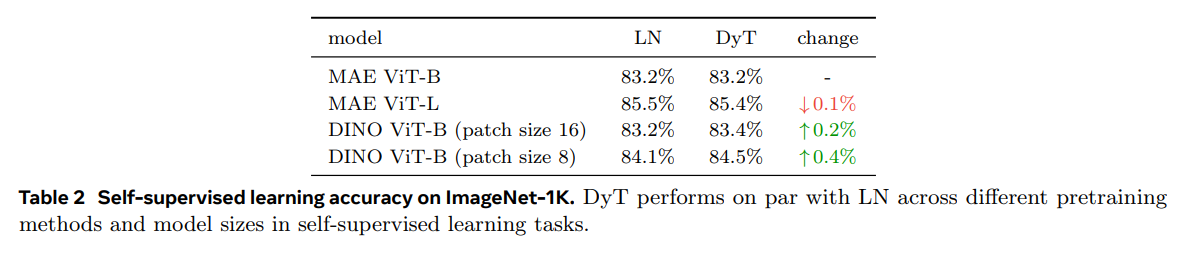
DyT는 자기 지도 학습 작업에서 LN과 동등한 성능을 지속적으로 발휘합니다.

DyT는 LN에 비해 동등하거나 향상된 FID를 달성합니다.
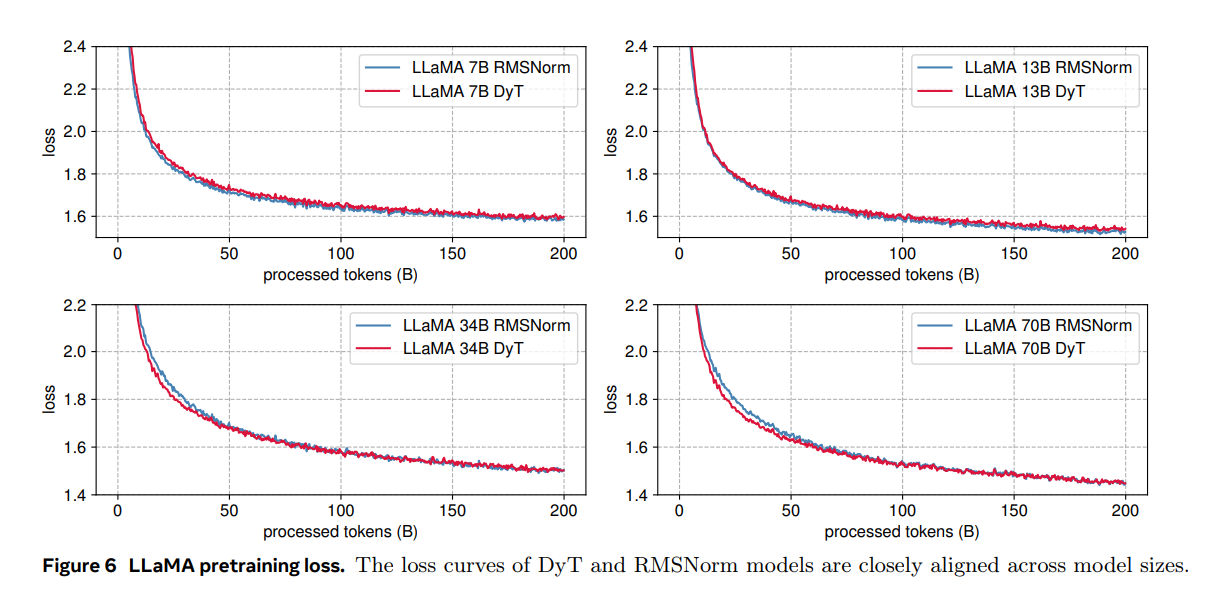

DyT는 모든 네 가지 모델 크기에서 RMSNorm과 동등한 성능을 보입니다.
그림 6은 손실 곡선을 나타내며, 모든 모델 크기에서 훈련 손실이 훈련 내내 밀접하게 일치하는 유사한 추세를 보여줍니다.

DyT는 Wav2Vec 모델 크기 모두에서 LN과 비슷한 성능을 보임을 관찰합니다.
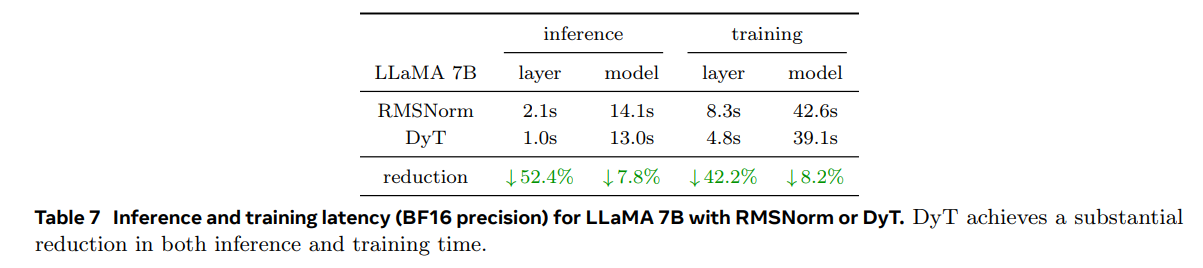
우리는 LLaMA 7B 모델을 RMSNorm 또는 DyT와 함께 벤치마킹하여 4096 토큰의 단일 시퀀스를 사용해 100번의 순방향 패스(추론)과 100번의 순방향-역방향 패스(훈련)에 소요된 총 시간을 측정합니다.
표 7은 Nvidia H100 GPU에서 BF16 정밀도를 사용할 때 모든 RMSNorm 또는 DyT 레이어와 전체 모델에 필요한 시간을 보고합니다.
DyT 레이어는 RMSNorm 레이어에 비해 계산 시간을 상당히 줄여주며, FP32 정밀도에서도 유사한 경향이 관찰됩니다.
DyT는 효율성 중심의 네트워크 설계에 유망한 선택이 될 수 있습니다.
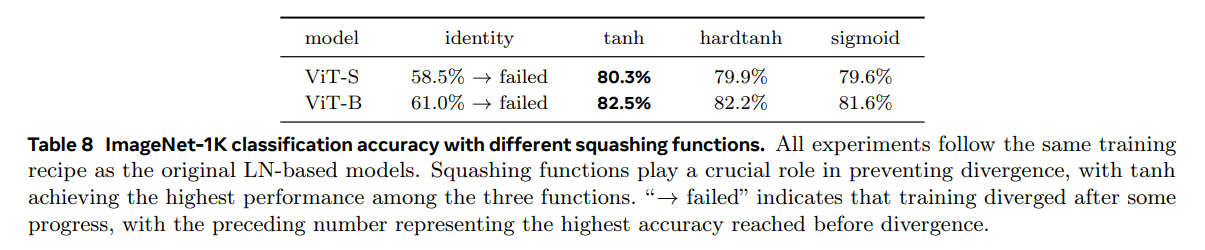
DyT 레이어에서 tanh를 대체 함수인 hardtanh와 sigmoid로 교체하면서 학습 가능한 스케일러 α는 그대로 유지합니다 (그림 7).
또한, tanh를 완전히 제거하고 정체 함수(identity function)로 교체하면서 α는 그대로 유지하는 경우를 평가합니다.
표 8에서 볼 수 있듯이, squashing 함수는 안정적인 훈련에 필수적입니다.
정체 함수를 사용하면 훈련이 불안정하고 발산하게 되며, squashing 함수는 안정적인 훈련을 가능하게 합니다.
여러 squashing 함수 중에서는 tanh가 가장 좋은 성능을 보였습니다.
이는 tanh가 부드럽고, 0을 중심으로 하는 특성 때문일 수 있습니다.

표 9에서 볼 수 있듯이, α를 제거하면 모든 squashing 함수에서 성능 저하가 발생하며, 이는 α가 전체 모델 성능에서 중요한 역할을 함을 강조합니다.
DyT의 효과를 더욱 평가하기 위해, 우리는 정규화 계층 없이 Transformer를 훈련할 수 있게 해주는 다른 방법들과 비교합니다.

우리는 α의 초기화(α0)가 성능에 미치는 영향이 거의 없다는 것을 발견했습니다.
유일한 예외는 LLM 훈련으로, 이 경우 α0의 세심한 조정이 눈에 띄는 성능 향상을 가져옵니다.
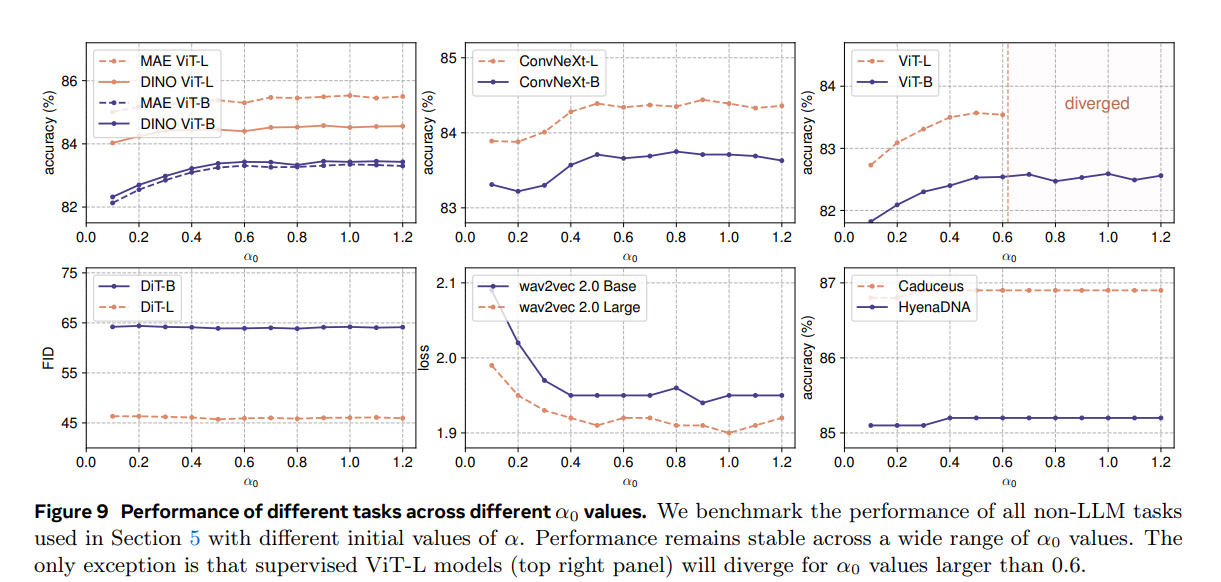
Non-LLM 모델은 α0에 대해 상대적으로 민감하지 않습니다.
그림 9는 다양한 작업에서 α0 값을 변경했을 때 검증 성능에 미치는 영향을 보여줍니다.
모든 실험은 해당 작업의 원래 설정과 하이퍼파라미터를 따릅니다.
우리는 α0 값이 0.5와 1.2 사이일 때 일반적으로 좋은 결과를 얻으며 성능이 안정적으로 유지됨을 관찰했습니다.
α0를 조정하는 것은 주로 훈련 곡선의 초기 단계에만 영향을 미칩니다.
주요 예외는 감독 학습된 ViT-L 실험으로, α0가 0.6을 초과하면 훈련이 불안정해지고 발산하게 됩니다.
이러한 경우, 학습률을 줄이면 안정성을 회복할 수 있습니다.
작은 α0 값은 더 안정적인 훈련을 초래합니다.
이전 관찰을 바탕으로 훈련 불안정성에 기여하는 요인을 추가로 분석했습니다.
우리의 발견에 따르면, 모델 크기나 학습률을 증가시키면 α0 값을 낮추어야 훈련을 안정적으로 유지할 수 있습니다.
반대로, α0 값이 높을 경우 훈련 불안정성을 완화하기 위해 학습률을 낮추어야 합니다.
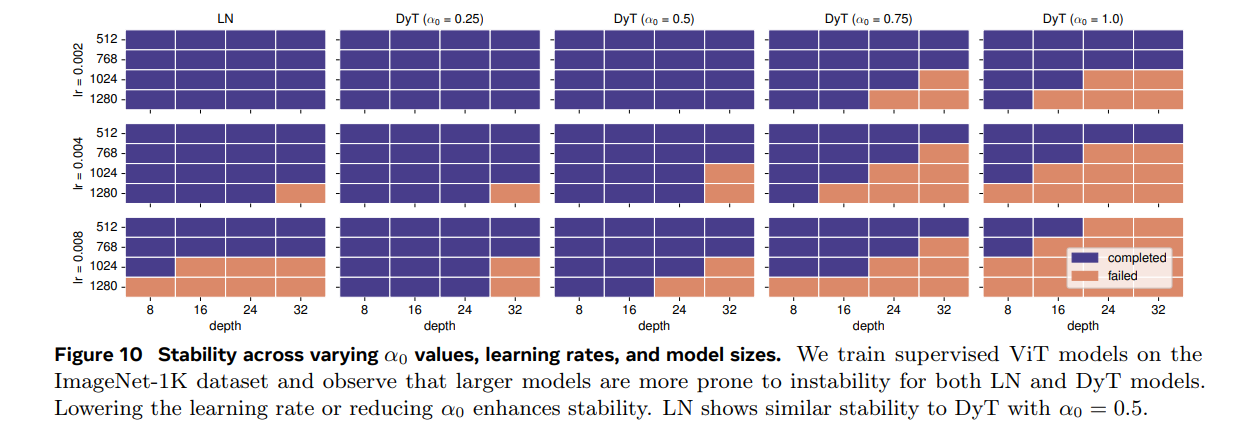
그림 10은 ImageNet-1K 데이터셋을 사용한 감독 학습된 ViT의 훈련 안정성에 대한 실험 결과를 보여줍니다.
학습률, 모델 크기, α0 값을 변화시켜 실험을 진행했습니다.
더 큰 모델을 훈련시키면 실패할 가능성이 더 크므로 안정적인 훈련을 위해 α0 값이나 학습률을 더 작게 설정해야 합니다.
비슷한 불안정성 패턴은 LN 기반 모델에서도 유사한 조건에서 관찰되었으며, α0 = 0.5로 설정하면 LN과 유사한 안정성 패턴을 보입니다.
우리의 발견을 바탕으로, 모든 비-LLM 모델에 대해 α0 = 0.5를 기본값으로 설정합니다.
이 설정은 LN과 유사한 훈련 안정성을 제공하면서도 강력한 성능을 유지합니다.
7.2 LLM에 대한 α 초기화
α0 조정은 LLM 성능을 향상시킵니다. 앞서 논의한 바와 같이, 기본 설정인 α0 = 0.5는 대부분의 작업에서 잘 작동합니다.
그러나 α0 값을 조정하면 LLM 성능을 상당히 향상시킬 수 있음을 알게 되었습니다.
우리는 LLaMA 모델들에서 α0를 조정하여 각 모델을 30B 토큰으로 사전 훈련시키고 훈련 손실을 비교했습니다.
표 11은 각 모델에 대해 조정된 α0 값을 요약한 것입니다. 두 가지 주요 발견이 있습니다:
- 더 큰 모델은 더 작은 α0 값을 요구합니다. 작은 모델에 대해 최적의 α0 값이 결정되면, 더 큰 모델에 대해 탐색 공간을 그에 맞게 줄일 수 있습니다.
- 어텐션 블록에 대해 더 높은 α0 값을 사용하면 성능이 향상됩니다. 우리는 어텐션 블록의 DyT 층에는 더 높은 α 값을, 다른 위치(예: FFN 블록이나 최종 선형 프로젝션 전에 있는 DyT 층)에는 더 낮은 α 값을 초기화하면 성능이 개선된다는 것을 발견했습니다.

모델의 너비는 α0 선택에 주로 영향을 미칩니다.
우리는 모델의 너비와 깊이가 최적의 α0에 미치는 영향을 조사했습니다.
그 결과, 모델 너비가 최적의 α0를 결정하는 데 중요한 역할을 하며, 모델 깊이는 미미한 영향을 미친다는 것을 발견했습니다.

더 넓은 네트워크가 최적의 성능을 위해 더 작은 α0 값을 필요로 한다는 것을 나타냅니다. 반면, 모델 깊이는 α0 선택에 거의 영향을 미치지 않습니다.
9 제한 사항
우리는 Transformer 및 다른 최신 아키텍처에서 널리 사용되는 LN 또는 RMSNorm을 사용하는 네트워크에서 실험을 수행했습니다.
예비 실험(부록 C 참조)에서는 DyT가 ResNet과 같은 고전적인 네트워크에서 BN을 직접 대체하는 데 어려움을 겪는다고 나타났습니다.
DyT가 다른 유형의 정규화 계층을 가진 모델에 어떻게 적응할 수 있는지에 대해서는 더 깊이 연구할 필요가 있습니다.
10 결론
이 연구에서는 특히 Transformer와 같은 최신 신경망이 정규화 계층 없이 훈련될 수 있음을 보여줍니다.
이는 전통적인 정규화 계층을 대체하는 간단한 방법인 동적 탄젠트(DyT)를 통해 이루어졌습니다.
DyT는 학습 가능한 스케일링 팩터 α를 통해 입력 활성화 범위를 조정한 후, S자 형태의 tanh 함수를 통해 극단적인 값을 압축합니다.
비록 더 단순한 함수이지만, 정규화 계층의 동작을 효과적으로 포착합니다.
다양한 설정에서 DyT를 사용한 모델은 정규화된 모델들과 동일하거나 그 이상의 성능을 보입니다.
이 결과는 현대 신경망 훈련에서 정규화 계층의 필요성에 대한 전통적인 이해에 도전합니다.
우리의 연구는 또한 심층 신경망에서 가장 기본적인 구성 요소 중 하나인 정규화 계층의 메커니즘에 대한 이해에 기여합니다.
https://arxiv.org/abs/2503.10622?utm_source=pytorchkr&ref=pytorchkr
Transformers without Normalization
Normalization layers are ubiquitous in modern neural networks and have long been considered essential. This work demonstrates that Transformers without normalization can achieve the same or better performance using a remarkably simple technique. We introdu
arxiv.org
https://github.com/meta-llama/llama/blob/main/llama/model.py
llama/llama/model.py at main · meta-llama/llama
Inference code for Llama models. Contribute to meta-llama/llama development by creating an account on GitHub.
github.com
https://github.com/jiachenzhu/DyT/blob/main/other_tasks/LLaMA/fms_fsdp/models/llama.py
DyT/other_tasks/LLaMA/fms_fsdp/models/llama.py at main · jiachenzhu/DyT
Code release for DynamicTanh (DyT). Contribute to jiachenzhu/DyT development by creating an account on GitHub.
github.com
논문저자들이 LLaMA의 DyT 부분을 이렇게 구현했는데
class LayerNormParameterized(nn.Module):
def __init__(self, normalized_shape, alpha_init_value):
super(LayerNormParameterized, self).__init__()
self.normalized_shape = normalized_shape
self.alpha_init_value = alpha_init_value
self.alpha = nn.Parameter(torch.empty(1))
self.weight = nn.Parameter(torch.empty(normalized_shape))
def reset_parameters(self):
self.alpha.data.fill_(self.alpha_init_value)
self.weight.data.fill_(1)
def forward(self, x):
return self.weight * torch.tanh(self.alpha * x)
def extra_repr(self):
return f"normalized_shape={self.normalized_shape}, alpha_init_value={self.alpha_init_value}"
원래 META의 LLaMA의 RMSNorm은..
class RMSNorm(torch.nn.Module):
def __init__(self, dim: int, eps: float = 1e-6):
"""
Initialize the RMSNorm normalization layer.
Args:
dim (int): The dimension of the input tensor.
eps (float, optional): A small value added to the denominator for numerical stability. Default is 1e-6.
Attributes:
eps (float): A small value added to the denominator for numerical stability.
weight (nn.Parameter): Learnable scaling parameter.
"""
super().__init__()
self.eps = eps
self.weight = nn.Parameter(torch.ones(dim))
def _norm(self, x):
"""
Apply the RMSNorm normalization to the input tensor.
Args:
x (torch.Tensor): The input tensor.
Returns:
torch.Tensor: The normalized tensor.
"""
return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)
def forward(self, x):
"""
Forward pass through the RMSNorm layer.
Args:
x (torch.Tensor): The input tensor.
Returns:
torch.Tensor: The output tensor after applying RMSNorm.
"""
output = self._norm(x.float()).type_as(x)
return output * self.weight
'AI 논문 > AI trend research' 카테고리의 다른 글
| Model Context Protocol(MCP) 개념 이해하기 (0) | 2025.04.01 |
|---|---|
| A Review of DeepSeek Models' Key Innovative Techniques (0) | 2025.03.28 |
| Introducing Instella: New State-of-the-art Fully Open 3B Language Models (0) | 2025.03.08 |
| The FFT Strikes Back: An Efficient Alternative to Self-Attention (0) | 2025.03.07 |
| SFT Memorizes, RL Generalizes: A Comparative Study of Foundation Model Post-training (0) | 2025.02.14 |

