길이가 n인 두 수열이 존재하는데 두 수열 사이 흐릿함은 두번째 수열을 뒤집어서, 같은 위치에 있는 두 수의 곱의 합이다
예를 들어
3 -4 -3
-3 0 5는 -3 0 5를 뒤집어서 5 0 -3으로 하고 같은 위치에 있는 원소끼리
5*3 + 0*-4 + -3*-3 = 9 + 15 = 24
앞에서부터 b개 뒤에서부터 e개를 지워서 두 수열의 흐릿함을 되도록 크게 만들고자 한다면, 최댓값을 구하고 b,e를 구한다
---------------------------------------------------------------------------------------------------------------
쉽게 생각할 수 있는건 앞에서부터 b개를 지우고 뒤에서부터 e개를 지웠을때 dp[b][e]라고 한다면
dp[b][e]를 모두 구해놓는것이다
앞에서부터 b개 지우고 뒤에서부터 e개 지우면 b번부터 n-e-1번까지 남아있으므로,
여기를 다시 순회해서 흐릿함을 구해서 저장해놓으면 되겠지
그리고 최댓값 지점을 구하면 O(N^3)에 가능하다
n = int(input())
A = list(map(int,input().split()))
B = list(map(int,input().split()))
dp = [[0]*n for _ in range(n)]
for i in range(n):
for j in range(i,n):
w = i
v = 0
for k in range(j,i-1,-1):
v += B[k]*A[w]
w += 1
dp[i][j] = v
dp[j][i] = v
value = -(10**18)
p,q = -1,-1
for b in range(n):
for e in range(n-b):
if value < dp[b][-1-e]:
value = dp[b][-1-e]
p = b
q = e
print(p,q)
print(value)
근데 조금 더 생각해보면 DP[L-1][R+1]과 DP[L][R]이 간단한 관계식이 있다
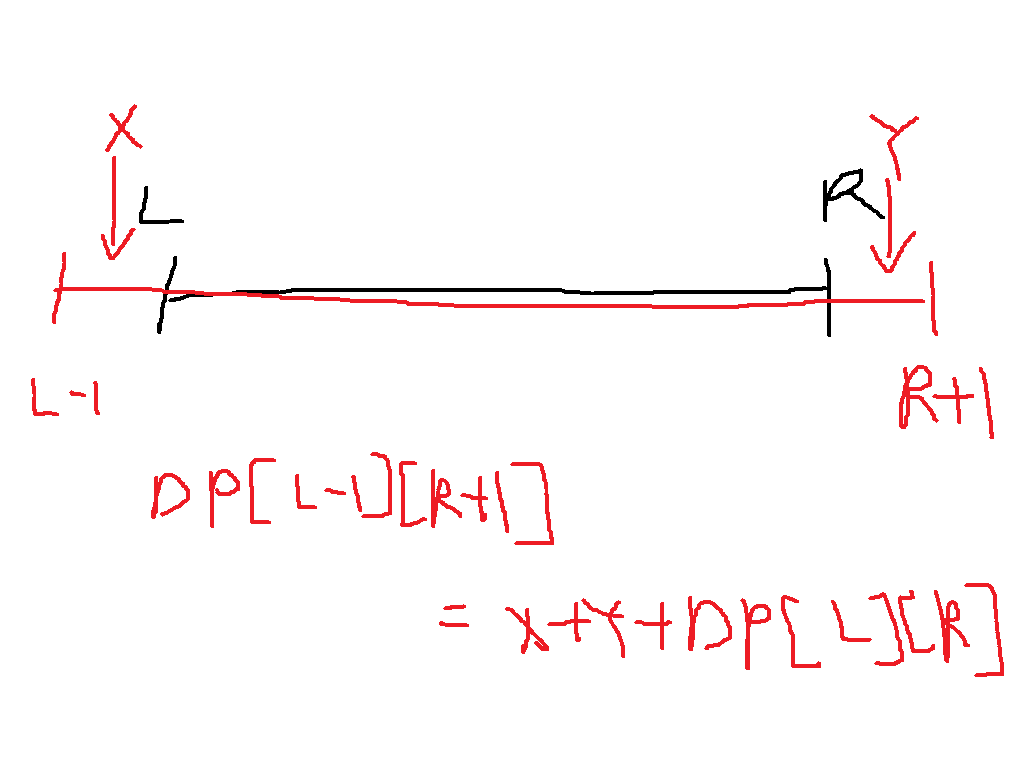
실제로 L-1~R+1부분과 L~R부분을 생각해보면 L-1~R+1부분은 L~R부분에다가 L-1번 R+1번이 더해진다
따라서 dp[L-1][R+1] = B[R+1]*A[L-1] + B[L-1]*A[R] + dp[L][R]
이때 L = R인경우는? L = R번인 원소만 남아있으니까 dp[L][R] = A[L]*B[R]
L,R이 (0,0), (0,1), (1,1),(1,2), (2,2), (2,3), ...(n-1,n-1),(n-1,n)으로 모두 해보면
각각의 경우에서 L -=1, R+=1을 해서 해보면 길이 N만큼 확장하고 (L,R)쌍은 O(N)개이므로, O(N^2)에 가능하다
n = int(input())
A = list(map(int,input().split()))
B = list(map(int,input().split()))
p,q = -1,-1
value = -(10**18)
for X in range(n):
#dp[L-1][R+1] = dp[L][R] + A[L-1]*B[R+1] + A[R+1]*B[L-1]
#L = R, dp[L][R] = A[L]*B[R]
for Y in range(X,X+2):
L,R = X,Y
if L == R:
v = -(A[L]*B[R])
else:
v = 0
while L >= 0 and R <= n-1:
v += (A[L]*B[R] + A[R]*B[L])
if value < v:
value = v
p = L
q = n-1-R
R += 1
L -= 1
print(p,q)
print(value)
L = R인 경우 v = -A[L]*B[R]해두면 while 들어가면서 2*A[L]B[R]이 더해지므로, A[L]B[R]만 남게된다
이렇게 더해나가면서 최댓값이 갱신되는 경우 두 지점 p,q도 기록해둔다
L~R까지 흐릿함을 계산하는 경우 앞에서 L개 제거한거고 뒤에서는 n-1-R개 제거한거라는거
--------------------------------------------------------------------------------------------------------------------------------------------------
근데 L,R이 (0,0), (0,1), (1,1),(1,2), (2,2), (2,3), ...(n-1,n-1),(n-1,n)으로 모두 해보면
각각의 경우에서 L -=1, R+=1을 해서 해보면 길이 N만큼 확장하고 (L,R)쌍은 O(N)개이므로, O(N^2)에 가능하다
(0,0), (0,1), (1,1),(1,2), (2,2), (2,3), ...(n-1,n-1),(n-1,n)로 하면 모든 경우를 검사할 수 있다는것 같은데
왜 그런걸까
잘 와닿지가 않는다
그냥 그려보면 (L,R) 좌표계에서 L <= R이므로, 왼쪽 위 격자점들을 찾아야하는데
L > R이면 이상하잖아 앞에서부터 L개 제거 뒤에서부터 R개 제거인데

L -= 1, R+=1은 왼쪽으로 1칸 위쪽으로 1칸 가야하므로,

근데 그런다고 하더라도 (0,0), (0,1), (1,1),(1,2),...를 검사해야한다고 생각하는게 어렵긴하네
'알고리즘 > 다이나믹 프로그래밍' 카테고리의 다른 글
| 스위치를 누른 효과가 j초 남아있는 지속시간 다이나믹 프로그래밍 (0) | 2025.04.07 |
|---|---|
| 양팔저울을 이용해서 무게를 알아낼 수 있는 추를 찾는 방법 (0) | 2025.04.04 |
| 연속하는 구간을 한번 뒤집어야할때 켜져있는 원소들의 합의 최댓값을 구하는 놀라운 방법 (0) | 2025.03.24 |
| 한번 쉬면 끝까지 쉬어야할 때 최대한 멀리 달리는 다이나믹 프로그래밍 (0) | 2025.03.19 |
| 길이가 K인 증가하는 부분 수열의 개수를 구하는 다이나믹 프로그래밍 (0) | 2025.03.11 |

