n분 동안 달리는데 1분 달리면 지침 지수가 1 올라간다
1분 쉬면 지침 지수가 1 내려간다
지침 지수가 m보다 커지면 달릴 수 없다
한번 쉬면 지침 지수가 0이 될 때까지 쉬어야한다
또한 달리기가 끝난 n분에 지침지수가 0이 되어야한다
i분에 달릴 수 있는 거리가 주어진다.
D = [5,3,4,2,10]이면 1분에 달리면 5만큼 뛰고 2분에 달리면 3만큼 뛴다는 소리
이때 가장 멀리 달릴 수 있는 거리는?
-------------------------------------------------------------------------------------------------------------------------------------------------
i번째 시간에 지침지수가 j이고 달리고 있는지 아닌지 여부 k에 대하여 dp[i][j][k]를 정의
처음에 달리면 dp[0][1][1] = D[0]
i시간에 달리는데 지침지수가 1이라면 지침지수가 0이고 쉬는 중일때 달려야하므로
dp[i][1][1] = dp[i][0][0] + D[i]
지침지수가 1보다 큰 경우에는 달리는 중이므로
dp[i][j+1][1] = dp[i-1][j][1] + D[i]
쉬면 지침지수가 1 줄어드는데, 쉬는 상태일때 지침지수가 j+1인 경우 쉴 수 있고,
달리는 상태일때 지침지수가 j+1인 경우 쉴 수 있으므로
dp[i][j][0] = max(dp[i-1][j+1][0], dp[i-1][j+1][1])
근데 애초에 dp값이 0으로 초기화 되어있기 때문에... dp라는 것은 이전 문제를 가지고 현재 문제를 해결해야하니
이전에 계산한 값을 가지고 와서 초기화를 해놓아야한다
dp[i][j][0] = dp[i-1][j][0]로 초기화하고
dp[i][j][0] = max(dp[i-1][j+1][0], dp[i-1][j+1][1])
정답은 마지막에 지침지수가 0이어야하므로 dp[n-1][0][0]
n,m = map(int,input().split())
D = []
for _ in range(n):
d = int(input())
D.append(d)
#dp[i][j][k] = i번째에 지침지수가 j이고 쉬면 k = 0, 달리면 k = 1
dp = [[[0,0] for _ in range(m+1)] for _ in range(n)]
dp[0][1][1] = D[0]
dp[0][0][0] = 0
for i in range(1,n):
#처음에 달려서 지침지수가 1이 되는 경우는
#처음에 쉬고 지침지수가 0인 경우에서 달려야
dp[i][1][1] = max(dp[i][1][1],dp[i-1][0][0] + D[i])
for j in range(m):
if j >= 1:
dp[i][j+1][1] = max(dp[i][j+1][1],dp[i-1][j][1] + D[i])
#달리다가 쉬는 경우, 쉬는 중에 쉬는 경우
dp[i][j][0] = dp[i-1][j][0] #쉬는 경우 초기화
dp[i][j][0] = max(dp[i][j][0],dp[i-1][j+1][1], dp[i-1][j+1][0])
print(dp[n-1][0][0])
근데 파이썬은 메모리 초과나더라
이번엔 2차원 배열로 dp[i][j] = i번째 시간에 지침지수가 j인 경우
달린다면 dp[i][j+1] = dp[i-1][j] + D[i]
이때 쉬는 경우가 문제인데 한번 쉬면 끝까지 쉬어야한다 이걸 어떻게 처리해?
이는 지침지수가 j일때 쉬기 시작했다면, 지침지수가 0이 되어야한다는 의미
i-j시간에 지침지수가 j인 경우 j시간 쉬면 지침지수가 0이 되므로
dp[i][0] = dp[i-j][j]
마찬가지로 dp가 이전 문제를 가지고 현재 문제를 해결해야하는데 i-1번째 시간에 최댓값을 구했고
이는 i번째 시간으로 넘어가야하니까 dp[i][0] = dp[i-1][0]로 초기화해두고
dp[i][0] = max(dp[i][0],dp[i-j][j])
n,m = map(int,input().split())
D = []
for _ in range(n):
d = int(input())
D.append(d)
#dp[i][j] = i번째에 지침지수가 j
dp = [[0]*(m+1) for _ in range(n)]
dp[0][1] = D[0]
for i in range(1,n):
#달리는 경우
for j in range(m):
dp[i][j+1] = max(dp[i][j+1],dp[i-1][j] + D[i])
#쉬는거 초기화
dp[i][0] = dp[i-1][0]
#i-j분에 j 지침지수가 있는데 j분 쉬면 i분에 지침지수가 0이 되는
for j in range(1,m+1):
if i-j >= 0:
dp[i][0] = max(dp[i][0],dp[i-j][j])
print(dp[n-1][0])
근데 1차원 배열로도 해결할 수 있다더라
dp[i] = i번째 시간까지 달린 최대 거리
먼저 i번째 시간에 달리지 않고 쉬는 경우 dp[i] = max(dp[i],dp[i-1])
여기는 그렇다쳐 쉬면 그냥 1시간 넘어가니까
달리는건 어떻게하지?
한번 쉬면 끝까지 쉬어야하는데?
지침지수 j = 1,2,...,m에 대하여
i번째 시간부터 j시간동안 달리고, j시간동안 쉬어서 i+2j-1시간에 달린 거리가 갱신되는지 체크
여기서 생각을 잘해야하는데
i번째 시간부터 j시간 달리고 j시간 쉬면 시간이 언제 되는지가 문제인데
대충 생각하면 i+2j시간이라고 생각할 수 있다

근데 i번째 시간을 포함해서 j시간 달리면 i,i+1,i+2,...,i+j-1이어야 j시간 달린거임
여기에 j시간 더 쉬면 i+2j-1이 된다는거
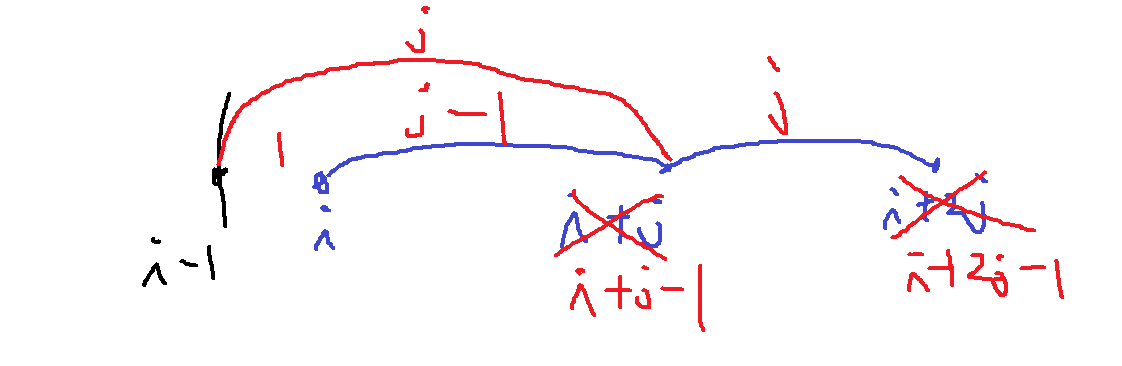
그래서 dp[i-1] + (i~i+2j-1에 달릴 수 있는 거리)
그러면 i~i+2j-1에 달릴 수 있는 거리를 O(1)에 구하기 위해 거리 배열 D의 누적합을 이용
dp[i-1] + D[i+2j-1] - D[i-1]로 구할 수 있다
from sys import stdin
n,m = map(int,stdin.readline().split())
A = []
for _ in range(n):
d = int(stdin.readline())
A.append(d)
D = [0,A[0]]
for i in range(1,n):
D.append(D[-1] + A[i])
dp = [0]*(n+1)
for i in range(1,n+1):
dp[i] = max(dp[i], dp[i-1])
for j in range(1,m+1):
if i+2*j-1 <= n:
dp[i+2*j-1] = max(dp[i+2*j-1], dp[i-1] + (D[i+j-1] - D[i-1]))
print(dp[n])
'알고리즘 > 다이나믹 프로그래밍' 카테고리의 다른 글
| 배열을 뒤집어서 다른 배열과 대응하는 원소끼리 곱의 합의 특징 (0) | 2025.04.03 |
|---|---|
| 연속하는 구간을 한번 뒤집어야할때 켜져있는 원소들의 합의 최댓값을 구하는 놀라운 방법 (0) | 2025.03.24 |
| 길이가 K인 증가하는 부분 수열의 개수를 구하는 다이나믹 프로그래밍 (0) | 2025.03.11 |
| 크기가 1씩 증가하는 가장 긴 증가하는 부분수열의 길이를 구하는 다이나믹 프로그래밍 (0) | 2025.03.10 |
| 두 팀중 적어도 한 팀이 소수만큼 점수를 얻을 확률 (0) | 2025.03.02 |

