n*n 배열이 주어질때, B*B 크기의 임의의 부분 행렬이 포함하는 정수 중 최댓값과 최솟값의 차이를 묻는 쿼리가 주어진다
이 쿼리에 답한다
---------------------------------------------------------------------------------------------------------------------------------------------------
https://deepdata.tistory.com/1457
임의의 직사각형에 포함된 서로 다른 정수의 개수를 찾는 2차원 배열 누적합
14846번: 직사각형과 쿼리 n*n 배열에서 왼쪽 위가 (x1,y1), 오른쪽 아래가 (x2,y2)인 직사각형에 포함되는 서로 다른 정수의 개수를 찾는 쿼리가 많이 주어질 때 이 쿼리에 답한다 -------------------------
deepdata.tistory.com
여기서 했던 테크닉 대로 배열이 포함하는 정수가 최대 250이므로, 250*250*250은 15625000으로 메모리 적당
그래서 dp[y][x][i]를 왼쪽 위가 (0,0), 오른쪽 아래가 (x,y)인 직사각형 내부가 포함하는 정수 i의 개수
이러면 O(N^3)에 전처리가 가능하고
from sys import stdin
n,b,k = map(int,stdin.readline().split())
maps = [list(map(int,stdin.readline().split())) for _ in range(n)]
dp = [[[0]*251 for _ in range(250)] for _ in range(250)]
dp[0][0][maps[0][0]] = 1
for y in range(1,n):
dp[y][0][maps[y][0]] += 1
for i in range(251):
dp[y][0][i] += dp[y-1][0][i]
for x in range(1,n):
dp[0][x][maps[0][x]] += 1
for i in range(251):
dp[0][x][i] += dp[0][x-1][i]
for y in range(1,n):
for x in range(1,n):
dp[y][x][maps[y][x]] += 1
for i in range(251):
dp[y][x][i] += (dp[y-1][x][i] + dp[y][x-1][i] - dp[y-1][x-1][i])
쿼리가 주어지면 어떻게 찾아야할까?
모든 i = 0,2,..,250에 대하여 직사각형이 포함하는 정수 i의 개수를 찾는다
dp[y+b-1][x+b-1][i] - dp[y-1][x+b-1][i] - dp[y+b-1][x-1][i] + dp[y-1][x-1][i]
이 값이 1이상이라면, 해당하는 정수 i가 존재한다는 뜻이다
이런식으로 정수 i가 존재한다면 최대, 최소를 갱신한다
모든 정수 i에 대해 체크했으면 최대 - 최소를 구하면 된다
이러면 O(KN)에 쿼리에 답할 수 있다
for _ in range(k):
y,x = map(int,stdin.readline().split())
y -= 1
x -= 1
max_value = 0
min_value = 300
for i in range(251):
v1 = dp[y+b-1][x+b-1][i]
if y >= 1:
v2 = dp[y-1][x+b-1][i]
else:
v2 = 0
if x >= 1:
v3 = dp[y+b-1][x-1][i]
else:
v3 = 0
if y >= 1 and x >= 1:
v4 = dp[y-1][x-1][i]
else:
v4 = 0
c = v1 - v2 - v3 + v4
if c >= 1:
if max_value < i:
max_value = i
if min_value > i:
min_value = i
print(max_value - min_value)
근데 사실 전처리를 O(N^3)에 가능한데, (x,y)만 알면 되니까 dp2[y][x]를 왼쪽 위가 (x,y)일때 문제에서 요구하는 최대 - 최소라고 정의하면
dp[y][x][i]를 이용한다면
모든 i = 0,2,..,250에 대해 dp[y+b-1][x+b-1][i] - dp[y-1][x+b-1][i] - dp[y+b-1][x-1][i] + dp[y-1][x-1][i]을 구해
존재하는 정수중 최대, 최소를 찾고, 해당 (x,y)에 대하여 dp2[y][x] = max - min으로 갱신
여기서 주의할 점은 (x,y)는 최대 n-b까지라는 점에 유의해야한다
이러면 전처리를 O(N^3), 쿼리에 O(K)에 해결하게 된다
dp2 = [[0]*n for _ in range(n)]
for y in range(n-b+1):
for x in range(n-b+1):
max_value = 0
min_value = 300
for i in range(251):
v1 = dp[y+b-1][x+b-1][i]
if y >= 1:
v2 = dp[y-1][x+b-1][i]
else:
v2 = 0
if x >= 1:
v3 = dp[y+b-1][x-1][i]
else:
v3 = 0
if y >= 1 and x >= 1:
v4 = dp[y-1][x-1][i]
else:
v4 = 0
c = v1 - v2 - v3 + v4
if c >= 1:
if max_value < i:
max_value = i
if min_value > i:
min_value = i
dp2[y][x] = max_value - min_value
for _ in range(k):
y,x = map(int,stdin.readline().split())
y -= 1
x -= 1
print(dp2[y][x])
근데 더 빠르게 O(N^2)에 전처리가 가능하다
슬라이딩 윈도우를 이용한 구간 최대,최소 찾기 트릭을 이용하면
https://deepdata.tistory.com/1223
슬라이딩 윈도우를 이용한 최댓값 찾기(sliding window maximum, Deque Range Maximum Trick)
1. 문제 배열 A에서 길이가 K인 모든 연속하는 부분배열내에서 최댓값을 찾는 문제 [1,2,3,1,4,5]이고 K = 3인 경우를 생각해보자. [1,2,3]에서 최댓값은 3 [2,3,1]에서 최댓값은 3 [3,1,4]에서 최댓값은 4
deepdata.tistory.com
maxrow[y][x]를 행 y에 대하여, x,x+1,x+2,...x+b-1 구간에서의 최댓값
minrow[y][x]를 행 y에 대하여 x,x+1,x+2,...,x+b-1 구간에서의 최솟값이라고 정의하고
maxqueue, minqueue를 이용해 위에서 배운 트릭을 이용하여 각각 찾아준다
from collections import deque
from sys import stdin
n,b,k = map(int,stdin.readline().split())
maps = [list(map(int,stdin.readline().split())) for _ in range(n)]
maxrow = [[0]*n for _ in range(n)]
minrow = [[0]*n for _ in range(n)]
for y in range(n):
max_queue = deque([])
min_queue = deque([])
j = 0
for i in range(b):
while max_queue and maps[y][i] >= maps[y][max_queue[-1]]:
max_queue.pop()
while min_queue and maps[y][i] < maps[y][min_queue[-1]]:
min_queue.pop()
max_queue.append(i)
min_queue.append(i)
maxrow[y][0] = maps[y][max_queue[0]]
minrow[y][0] = maps[y][min_queue[0]]
j += 1
for x in range(b,n):
while max_queue and x-b >= max_queue[0]:
max_queue.popleft()
while min_queue and x-b >= min_queue[0]:
min_queue.popleft()
while max_queue and maps[y][x] >= maps[y][max_queue[-1]]:
max_queue.pop()
while min_queue and maps[y][x] < maps[y][min_queue[-1]]:
min_queue.pop()
max_queue.append(x)
min_queue.append(x)
maxrow[y][j] = maps[y][max_queue[0]]
minrow[y][j] = maps[y][min_queue[0]]
j += 1
다음 maxdp[y][x] = 왼쪽 위가 (x,y)일때 B*B 크기의 부분행렬의 최댓값
mindp[y][x] = 왼쪽 위가 (x,y)일때 B*B 크기의 부분행렬의 최솟값
이라고 한다면,
열 x에 대하여 y,y+1,y+2,...,y+b-1 행에서 최댓값인 maxrow[y][x], maxrow[y+1][x],...,maxrow[y+b-1][x]는
(x,y)에서 B*B 크기의 부분행렬의 최댓값 후보들이다
이들중 최댓값이 (x,y)에서 B*B 크기의 부분행렬의 최댓값
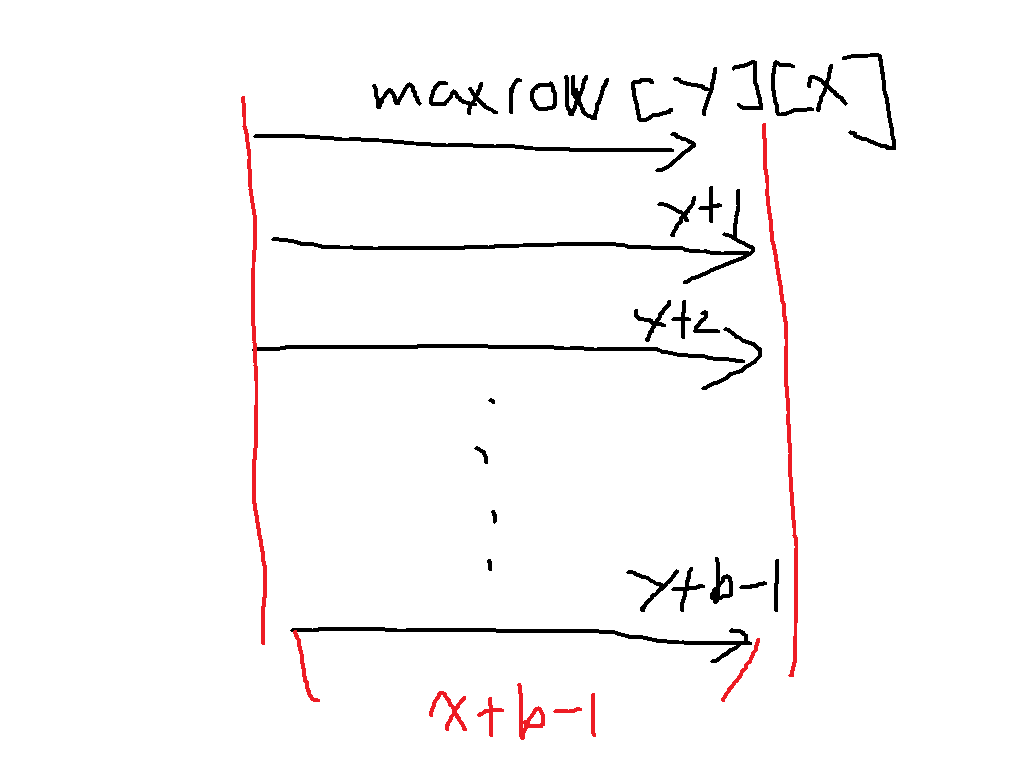
마찬가지로 mindp[y][x]는 minrow[y][x], minrow[y+1][x], ... minrow[y+b-1][x]중 최솟값으로 구할 수 있다
이 역시 deque를 이용한 구간 트릭으로 빠르게 찾는다
maxdp = [[0]*n for _ in range(n)]
mindp = [[0]*n for _ in range(n)]
for x in range(n):
max_queue = deque([])
min_queue = deque([])
j = 0
for i in range(b):
while max_queue and maxrow[i][x] >= maxrow[max_queue[-1]][x]:
max_queue.pop()
while min_queue and minrow[i][x] < minrow[min_queue[-1]][x]:
min_queue.pop()
max_queue.append(i)
min_queue.append(i)
maxdp[0][x] = maxrow[max_queue[0]][x]
mindp[0][x] = minrow[min_queue[0]][x]
j += 1
for y in range(b,n):
while max_queue and y-b >= max_queue[0]:
max_queue.popleft()
while min_queue and y-b >= min_queue[0]:
min_queue.popleft()
while max_queue and maxrow[y][x] >= maxrow[max_queue[-1]][x]:
max_queue.pop()
while min_queue and minrow[y][x] < minrow[min_queue[-1]][x]:
min_queue.pop()
max_queue.append(y)
min_queue.append(y)
maxdp[j][x] = maxrow[max_queue[0]][x]
mindp[j][x] = minrow[min_queue[0]][x]
j += 1
이러면 maxdp[y][x]와 mindp[y][x]가 (x,y)에서 B*B 크기의 부분행렬이 가지는 최댓값과 최솟값이므로
쿼리에 O(1)에 답할 수 있어서 O(N^2 + K)에 해결가능
for _ in range(k):
y,x = map(int,stdin.readline().split())
y -= 1
x -= 1
print(maxdp[y][x] - mindp[y][x])
'알고리즘 > 누적 합 알고리즘' 카테고리의 다른 글
| 임의의 직사각형에 포함된 서로 다른 정수의 개수를 찾는 2차원 배열 누적합 (0) | 2025.02.07 |
|---|---|
| 높이가 작은 인접한 성냥으로 불을 옮길 때 가장 많은 성냥에 불을 태우는 방법 (0) | 2024.08.21 |
| 누적 합으로 i < j < k < l을 돌아버리는 미친 다이나믹 프로그래밍 테크닉 (0) | 2024.07.16 |
| 코딩테스트 복기 - 구간합이 전부 똑같도록 3구간으로 나누는 방법(잘 모를때는 조건식을 써봐라) (0) | 2024.04.27 |
| prefix sum만이 누적합이 아니다1 - value 누적합 (0) | 2024.04.10 |

