슬라이딩 윈도우를 이용한 최댓값 찾기(sliding window maximum, Deque Range Maximum Trick)

1. 문제

 

배열 A에서 길이가 K인 모든 연속하는 부분배열내에서 최댓값을 찾는 문제

 

[1,2,3,1,4,5]이고 K = 3인 경우를 생각해보자.

 

[1,2,3]에서 최댓값은 3

 

[2,3,1]에서 최댓값은 3

 

[3,1,4]에서 최댓값은 4

 

[1,4,5]에서 최댓값은 5

 

배열의 크기가 작으면 매우 쉬운 문제지만, 배열의 크기가 크면 상당히 어려운 문제다.

 

투포인터로 구간의 시작과 끝을 잡고 첫 구간에서는 어떻게 O(K)로 최댓값을 찾아 놓은 다음..

 

다음 구간으로 이동할텐데, 시작과 끝의 위치를 아니까, 시작 쪽의 원소를 버릴거고

 

끝의 원소를 추가할거고... 그런다고 하더라도 최댓값이 뭔지를 어떻게 알지?

 

운 좋게 시작과 끝에 최댓값이 있다고 하더라도... 구간 중간에 최댓값이 있는거라면 어쨌든 매 구간마다 O(K)로 찾아야하나?

 

 

 

2. deque를 이용한 해법

 

해법이 heap, set, deque를 이용한 방법 등 여러가지가 있다..

 

https://www.geeksforgeeks.org/sliding-window-maximum-maximum-of-all-subarrays-of-size-k/

Sliding Window Maximum (Maximum of all subarrays of size K) - GeeksforGeeks

 

 

deque가 제일 빠른 것 같고 구현이 간단하니 이 방법을 일단 공부하자

 

이 방법의 핵심은 deque의 첫번째 원소에 구간의 최댓값의 인덱스를 저장해놓는 것이다.

 

[1,2,3,1,4,5]를 예로 들어 생각해보자

 

처음에는 인덱스 0부터 길이 K = 3만큼 순회해서... [1,2,3]에서 최댓값의 인덱스가 2이므로, deque에 2를 저장

 

여기서 원소 3을 저장해도 되는거 아니냐? 할 수 있는데 인덱스를 저장해야 나중에 필요하다..

 

 

 

다음 위치로 이동하는데... 0,1,2 인덱스에서 1,2,3 인덱스로 이동하면... 버려지는 원소는 0번

 

추가되는 원소는 3번이다.

 

0번은 버려야하기 때문에, deque의 왼쪽을 검사했을 때, 0번보다 작거나 같은 인덱스가 존재한다면?

 

그 인덱스는 이제 검사하는 구간 1,2,3에는 필요없으므로 제거해야한다.

 

이래서 deque에 원소를 저장하는게 아니라 인덱스를 저장해야한다.

 

아무튼 deque에는 2가 저장되어 있는데 0보다 크니까 버려지는 원소는 아니니 넘어가고

 

 

 

이제 3번 원소를 추가해야하는데, 2번 원소 3과 비교했을 때 3번 원소 1은 더 작으니 추가되지 않는다.

 

그래서 여전히 이 구간에서도 2번 인덱스 원소가 최댓값

 

 

다음 구간 2,3,4로 이동하는데 이제 버려지는 원소는 1번 인덱스, 추가되는 원소는 4번 인덱스

 

deque 왼쪽을 검사해서 1보다 작거나 같은 인덱스를 찾아서 버려야한다.

 

2는 1보다 크니까, 버려지는 인덱스는 없다.

 

다음 4번 원소가 추가되는데, 4번 원소 4와 deque에 최댓값으로 저장된 2번 원소 3을 비교해서 4가 더 크니까

 

deque에서 2번 인덱스를 제거하고 4번 인덱스를 추가

 

 

 

그러면 이 구간에서 최댓값은 4번 원소 4이다.

 

다음 구간 3,4,5로 이동한다.

 

버려지는 원소는 2번 인덱스, 추가되는 원소는 5번 인덱스

 

deque의 왼쪽에서 2번 인덱스보다 작거나 같은 인덱스가 있는지 검사하는데 4번 인덱스는 크므로, 제거하지 않는다.

 

deque 오른쪽에서 5번 인덱스 원소 5와 4번 인덱스 4를 비교해서 5가 더 크니까, 4를 제거하고 인덱스 5를 저장.

 

 

 

 

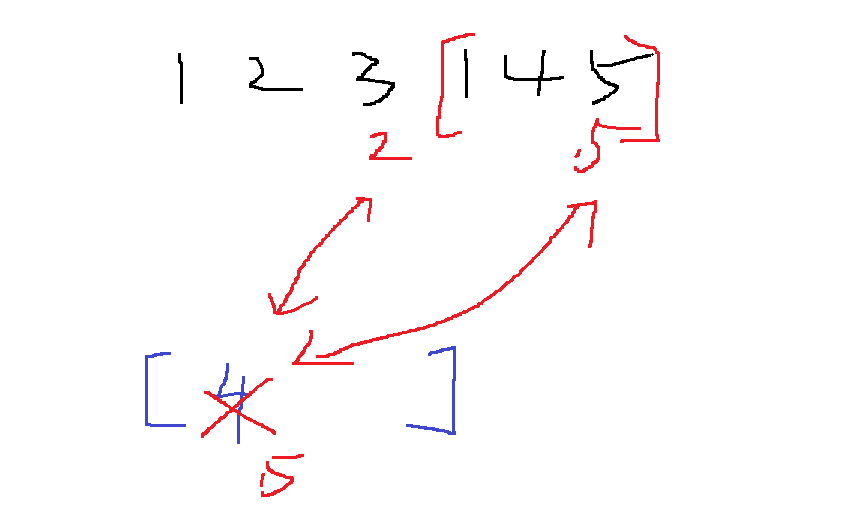
이렇게 하면 O(N)에 모든 부분구간에서 최댓값을 찾을 수 있다

 

O(N)보다 커보이기도 하는데.. 배열의 모든 원소가 추가되거나 제거되거나 각각 최대 1번씩 가능하므로, 

 

아무리 많아야 2N번 연산하기 때문에 O(N)이다

 

 

3. 구현

 

1) deque를 초기화

 

2) 처음 0번부터 K-1번까지 배열 A를 순회해서 각각 i번 원소에 대하여,

 

2-1) deque가 비어있지 않고,  deque의 맨 오른쪽 원소에 대해 A[i] >= A[deque[-1]]이면, 반복적으로 deque.pop()을 한다.

 

2-2) 2-1)이 끝나면 인덱스 i를 deque에 추가

 

3) 다시 K번부터 N-1번까지 배열 A를 순회해서... i번 인덱스에 대하여...

 

추가되는 원소는 i번이고 버려지는 원소는 i-k번 이다.

 

3-1) A[deque[0]]가 현재 구간 [i-k,i-1]에서의 최댓값이다.

 

3-2) 먼저 deque가 비어있지 않고, deque의 맨 왼쪽 원소에 대해 i-k >= deque[0]이면, 반복적으로 deque.popleft()를 한다.

 

3-3) deque가 비어있지 않고, deque의 맨 오른쪽 원소에 대해 A[i] >= A[deque[-1]]이면, 반복적으로 deque.pop()을 한다.

 

3-4) 3-2)가 끝나면 인덱스 i를 deque에 추가

 

4) 3)이 끝나고 마지막에 A[deque[0]]가 맨 마지막 구간 [n-1-k,n-1]에서 최댓값

 

from collections import deque

n,k = map(int,input().split())

A = list(map(int,input().split()))

queue = deque()

for i in range(k):
    
    while queue and A[i] >= A[queue[-1]]:
            
        queue.pop()
    
    queue.append(i)

for i in range(k,n):
    
    print(A[queue[0]],end=' ')
    
    while queue and i-k >= queue[0]:
        
        queue.popleft()
    
    while queue and A[i] >= A[queue[-1]]:
        
        queue.pop()
    
    queue.append(i)

print(A[queue[0]],end=' ')

 

 

4. 연습문제1

 

11003번: 최솟값 찾기 (acmicpc.net)

 

A에서 연속된 길이 L인 모든 부분구간에서 최솟값을 찾아야하는 문제

 

위에서는 최댓값을 구하는 방법을 이야기 했지만, 사실 최솟값도 똑같이 하면 된다.

 

deque의 맨 첫번째 원소 deque[0]에 최솟값의 인덱스만 저장하면 똑같다.

 

그냥 이 문제 특징으로 Di = Ai-L+1 ~ Ai의 최솟값으로 정의했을 때, i = 1부터 하면 A1-L+1 = A2-L에서 2-L은 음수일 수 있잖아..

 

Ai에서 i가 0이하라면, 무시하라 이거임

 

그래서 처음에 그냥 l-1 길이 만큼 INF를 추가해놓으면 될 것이다.

 

INF = 10000000000000

A = [INF]*(l-1) + list(map(int,stdin.readline().split()))

 

 

나머지는 동일

 

from collections import deque
from sys import stdin

n,l = map(int,stdin.readline().split())

INF = 10000000000000

A = [INF]*(l-1) + list(map(int,stdin.readline().split()))

n = n + l - 1

queue = deque([])

for i in range(l):
    
    while queue and A[i] < A[queue[-1]]:
            
        queue.pop()
        
    queue.append(i)

for i in range(l,n):
    
    print(A[queue[0]],end=' ')

    while queue and i-l >= queue[0]:
            
        queue.popleft()
        
    while queue and A[i] < A[queue[-1]]:
            
        queue.pop()
        
    queue.append(i)

print(A[queue[0]], end=' ')

 

 

5. 연습문제2

 

https://atcoder.jp/contests/abc352/tasks/abc352_d

D - Permutation Subsequence

 

 

어떤 순열이 주어지는데, 그 순열에서 길이 k인 부분 구간을 잡는다.

 

여기서 부분 구간은 연속된 구간이 아니다.

 

여기서 부분구간이 연속된 정수들로만 이루어져있을 때, 그러한 부분구간 길이의 최솟값을 찾는 문제..

 

문제 그대로 접근할려고 하면 굉장히 어렵다

 

[2,3,1,4]에서 [2,3]이랑 [2,..1], [3,..,4] 3개 있는데.. 2부터 시작했을때, 2와 연속된 정수는 왼쪽으로 1,0,..

 

오른쪽으로 3,4,... 이렇게 있고.. 3부터 시작했을 때 3과 연속된 정수는 왼쪽으로 2,1,0,..., 오른쪽으로 4,5,6,...

 

---------------------------------------------------------------------------------------------------------------------------------------------------

 

근데 조금 바꿔서 생각하면... 배열이 순열이기 때문에 결국 원하는건

 

[1,2,3,4]에서 [1,2], [2,3], [3,4]를 찾으면 된다.

 

그래서 배열 [2,3,1,4]를 한번 순회해서 1,2,3,4의 인덱스 위치 [2,0,1,3]으로 바꿔준다.

 

이렇게 하면 [2,0,1,3]에서 길이 2인 부분구간을 sliding window로 찾으면 [2,0],[0,1],[1,3]인데..

 

각각 [1,2], [2,3], [3,4]를 나타내므로 조건을 만족시키는 구간이 된다.

 

 

그러면 각 구간의 길이는 [2,0]은 2-0 = 2이고 [0,1]은 1-0 = 1이고 [1,3]은 3-1 = 2이다.

 

즉 해당 부분구간 내의 최댓값 - 최솟값이 구간의 길이가 된다.

 

 

따라서 먼저 배열을 인덱스 배열로 바꿔주고,

 

매 부분구간마다 최댓값을 찾은 deque, 최솟값을 찾는 deque 2개를 이용해서 최댓값 - 최솟값을 찾아주면 된다

 

from collections import deque

n,k = map(int,input().split())

P = list(map(int,input().split()))

ind = [0]*n

for i in range(n):
    
    ind[P[i]-1] = i
 
max_queue = deque()
min_queue = deque()

for i in range(k):
    
    while max_queue and ind[i] >= ind[max_queue[-1]]:
            
        max_queue.pop()
    
    while min_queue and ind[i] <= ind[min_queue[-1]]:
            
        min_queue.pop()
        
    max_queue.append(i)
    min_queue.append(i)

answer = 100000000000000000000000000000

for i in range(k,n):

    d = ind[max_queue[0]] - ind[min_queue[0]]

    if d < answer:

        answer = d

    while max_queue and i-k >= max_queue[0]:

        max_queue.popleft()

    while max_queue and ind[i] >= ind[max_queue[-1]]:
            
        max_queue.pop()

    while min_queue and i-k >= min_queue[0]:

        min_queue.popleft()
        
    while min_queue and ind[i] <= ind[min_queue[-1]]:
            
        min_queue.pop()
        
    max_queue.append(i)
    min_queue.append(i)    

if ind[max_queue[0]] - ind[min_queue[0]] < answer:
    
    answer = ind[max_queue[0]] - ind[min_queue[0]]

print(answer)