25427번: DKSH를 찾아라 (acmicpc.net)
문자열 S가 주어질때, 인덱스 a < b < c < d에 대하여 S[a] + S[b] + S[c] + S[d] = 'DKSH'가 되는 (a,b,c,d)의 개수를 찾는 문제
N이 10만이라 4중 for문으로 찾으면 당연히 시간초과
문자열이 'DDDDKKK'로 이루어질때, 만들 수 있는 'DK'의 개수는?
인덱스를 기준으로 세볼 때
(0,4), (0,5), (0,6)
(1,4), (1,5), (1,6)
(2,4), (2,5), (2,6)
(3,4), (3,5), (3,6)
K를 기준으로 본다면,
(0,4), (1,4), (2,4), (3,4)
(0,5), (1,5), (2,5), (3,5)
(0,6), (1,6), (2,6), (3,6)
처음에 D의 개수를 하나씩 세다가, K를 만나면 그 동안 만난 D의 개수를 누적해서 더해주면 된다
어떤 문자열이 주어지면, D의 위치 인덱스를
(s1), (s2), (s3), (s4), .... (sd)
그러다가 K를 처음으로 만나면 위 순서쌍에 K의 위치를 넣어주면 된다
(s1,sk), (s2,sk), (s3,sk), .... , (sd,sk)
이러면 현재 d개를 찾은 것이고
두번째로 K를 만나면...
(s1), (s2), (s3), (s4), .... (sd)
(s1), (s2), (s3), (s4), .... (sd)
두 줄을 만들고 이 순서쌍에 K의 위치 인덱스들을 각각 넣어주면
(s1,sk), (s2,sk), (s3,sk), .... , (sd,sk)
(s1,sk'), (s2,sk'), (s3,sk'), .... , (sd,sk')
이러면 d + d개를 찾은 것이 될 것이고
그러다가 S를 처음으로 만난다면?
S의 위치 인덱스를 위 순서쌍에 모두 넣어주면 된다
(s1,sk,ss), (s2,sk,ss), (s3,sk,ss), .... , (sd,sk,ss)
(s1,sk',ss), (s2,sk',ss), (s3,sk',ss), .... , (sd,sk',ss)
이러면 아직 d+d개를 찾은 것이 될 것이고
그러다가 2번째 S의 위치를 또 찾게 된다면?
(s1,sk,ss), (s2,sk,ss), (s3,sk,ss), .... , (sd,sk,ss)
(s1,sk',ss), (s2,sk',ss), (s3,sk',ss), .... , (sd,sk',ss)
(s1,sk,ss'), (s2,sk,ss'), (s3,sk,ss'), .... , (sd,sk,ss')
(s1,sk',ss'), (s2,sk',ss'), (s3,sk',ss'), .... , (sd,sk',ss')
원래 d+d개의 순서쌍에서 ss를 빼버리고 새로운 ss'을 넣어주면 된다
그러면 d+d + d+d개를 찾게 되는데
마지막으로 H의 위치를 찾게 되면 이 모든 순서쌍에 H의 위치를 넣기만 하면 되므로, 총 d+d+d+d개를 찾게 된다
이것이 DKSH의 개수가 된다
따라서 문자열을 순회하면서 D의 개수를 하나씩 누적하다가...
처음으로 K를 만나면 K의 개수에 그 동안 만난 D의 개수를 더해주고
그러다가 D를 또 만나면 D의 개수 + 1
그러다가 K를 만나면 지금까지 센 D의 개수를 또 누적해주고...
다시 처음으로 S를 만나면 S의 개수에 누적된 K의 개수를 더해주고...
그러다가 D를 만나면? D의 개수 + 1
그러다가 K를 만나면? K의 개수에 D의 개수를 더해주고...
그러다가 D를 만나면? D의 개수 +1
...
처음으로 H를 만나면 H의 개수에 누적된 S의 개수를 더해주고
....
모든 문자열을 순회하면 H의 개수가 정답이 된다
이렇게 하면 a < b < c < d인 (a,b,c,d)의 개수를 찾는 문제를 O(N)에 해결할 수 있게 된다
n = int(input())
S = input()
d = 0
k = 0
s = 0
h = 0
for i in range(n):
if S[i] == 'D':
d += 1
elif S[i] == 'K':
k += d
elif S[i] == 'S':
s += k
elif S[i] == 'H':
h += s
print(h)
2. 비슷한 문제
24956번: 나는 정말 휘파람을 못 불어 (acmicpc.net)
비슷한 문제인데 이번엔 문자열에서 WHEEEEEEE....의 개수를 찾는 문제
WH까지는 고정이고 뒤에 E가 최소 2개 이상 붙어야한다
위와 비슷한 논리로 W를 만나면 W의 개수에 +1을 누적해주고...
H를 만나면 H의 개수에 W의 개수를 누적해주고...
근데 이제 E를 만나면 현재까지 만든 WH의 개수는 h에 저장이 되어 있는데... 이 문자열에 E를 최소 2개이상 붙여야한다
그러면 현재 E를 만난 위치 i 이후로 E가 몇개 있는지 알아야겠지?
그래서 처음에 E의 위치를 모두 찾아둔다
n = int(input())
s = input()
E = []
for i in range(n):
if s[i] == 'E':
E.append(i)
그러면 E에는 E의 위치들이 저장되어 있는데
W....H...E..................에서 처음으로 E를 만난 위치가 i라면... i이후로 E가 몇개나 있는지 알 수 있다
E에서 순회해서 i랑 같게되는 E[j] = i인 j를 찾으면 len(E) - j가 현재 i 이후로 E의 개수가 될 것이다
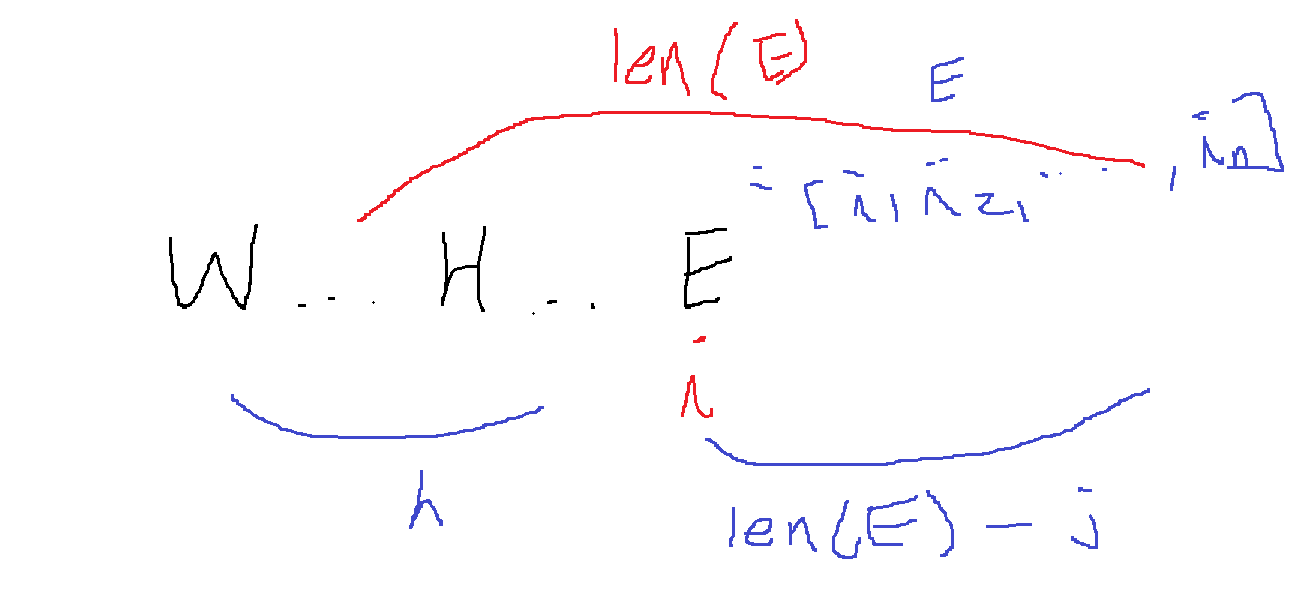
그러면 만든 WH에서 E를 적어도 2개이상 붙여야하므로,
len(E) - j개의 E에서 적어도 2개 이상의 E를 뽑는 경우의 수는?
전체 len(E) - j개의 원소로 부분집합을 만드는 경우의 수 2**(len(E) - j)에서
1개의 E를 뽑는 경우의 수 + 0개의 E를 뽑는 경우의 수 = len(E) - jC1 + len(E) -jC0 = len(E)-j+1을 빼주면 될 것
현재까지 만든 WH 문자열에 E를 2개 이상 뽑는 경우의 수를 곱해주면 WHEE.......를 만들 수 있을 것이다
그리고 나서 WH는 이미 썼으므로 0으로 초기화해줘야한다
W는 그대로 두고 그 이후에 나오는 H는 새롭게 써서 붙여줘야하므로...
mod = 10**9+7
w = 0
h = 0
k = 0
count = 0
for i in range(n):
if s[i] == 'W':
w += 1
w %= mod
elif s[i] == 'H':
h += w
h %= mod
elif s[i] == 'E':
for j in range(k,len(E)):
if E[j] == i:
k = j
break
e = len(E)-j
h *= ((pow(2,e,mod) - (e+1)%mod) % mod)
h %= mod
count += h
h = 0
print(count)
e가 클 수 있어서 pow함수로 mod연산을 해주면 속도를 빠르게 할 수 있다
근데 조금 다른 방법으로
W를 만나면 W의 개수에 +1
H를 만나면 H의 개수에 W의 개수를 누적해서 WH를 만들고
이제 처음으로 E를 만나면...
지금까지 만든 WHEE...의 개수가 answer개라고 해보자
1) 현재 만난 E를 지금까지 만든 answer개의 WHEE.... 뒤에 붙이더라도 조건을 만족하므로
현재 answer개에 새로운 answer개를 또 만들 수 있다
2) 그리고 지금까지 만든 WHE의 개수 e개에 E를 붙이면 WHEE로 이것도 조건을 만족하므로
최종적으로 answer개에 answer + e개의 새로운 문자열을 만들 수 있게 된다
그리고 나서 지금까지 만든 WH에 E를 붙이면 WHE를 만들 수 있으므로 E에 H를 누적해주고 다음으로 넘어가면 된다
n = int(input())
s = input()
w = 0
h = 0
e = 0
answer = 0
mod = 10**9+7
for i in range(n):
if s[i] == 'W':
w += 1
elif s[i] == 'H':
h += w #WH의 개수
elif s[i] == 'E':
#원래 WHEE...의 개수(answer)에 E를 붙이면 그만큼 늘어나므로...
#WHE의 개수 e에 E를 붙이면 WHEE가 되므로..
answer += (answer+e)
answer %= mod
e += h
print(answer)
e += h하고 answer += (answer+e)를 해야하나?
answer += (answer+e)를 하고 e+=h를 해야하나?
e는 지금까지 만든 WHE의 개수
answer은 WHEE...의 개수
E를 처음으로 만난 순간 지금까지 만난 WHE의 개수에 E를 붙이기만 하면 WHEE를 만들 수 있고
WHEE...의 개수에 E를 붙이기만 하면 WHEE....를 또 만들 수 있으니 먼저 answer += (answer+e)를 하고나서...
현재 만들어진 WH의 개수 h에 E를 붙이면 WHE를 만들 수 있으므로 e에 +=h를 하는게 순서에 맞다
e+=h를 먼저 하면 지금까지 만들어진 WH의 개수에 E를 붙인 WHE의 개수가 e에 더해지고...
answer += (answer+e)를 하게 되면 지금까지 만들어진 WHE의 개수에 E를 붙여서 WHEE를 더하게 되는데...
이는 원래 지금까지 만들어진 WH의 개수에 E를 2번이나 붙이게 된 경우를 더하게 되므로 잘못되었다
'알고리즘 > 누적 합 알고리즘' 카테고리의 다른 글
| 임의의 직사각형에 포함된 서로 다른 정수의 개수를 찾는 2차원 배열 누적합 (0) | 2025.02.07 |
|---|---|
| 높이가 작은 인접한 성냥으로 불을 옮길 때 가장 많은 성냥에 불을 태우는 방법 (0) | 2024.08.21 |
| 코딩테스트 복기 - 구간합이 전부 똑같도록 3구간으로 나누는 방법(잘 모를때는 조건식을 써봐라) (0) | 2024.04.27 |
| prefix sum만이 누적합이 아니다1 - value 누적합 (0) | 2024.04.10 |
| 구간에 원소를 더하는 쿼리가 많이 주어질 때 필요한 누적합 테크닉(imos법) (0) | 2024.03.31 |

