1. Bernoulli distribution
coin flip, head and tail
확률변수 값이 0 또는 1로 나타나는 분포
X ~ Ber(p)라고 표시
베르누이 분포는 p라는 모수 하나만 있으면 표현이 가능하다.
P(X=1) = p라 하면 자동적으로 P(X=0) = 1-p이 결정되니까

2. Categorical distribution
m-sided dice
Bernoulli distribution의 확장판
확률변수 값이 1,2,3,...,m중 하나를 가질 수 있는 분포
Y~ Cat(p1,p2,...,pm)으로 표시
이 분포를 표현하기 위해 필요한 parameter의 수는 m-1개이다.
왜냐하면 각 카테고리별로 확률을 부여하면
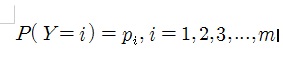
이렇게 쓸 수 있어 필요한 모수의 수가 m개같이 보이지만 제약조건으로 $\sum_{i=1}^{m}p_{i} = 1$
이 있으니까 m-1개 확률 값들이 결정되면 나머지 1개가 자동적으로 결정된다
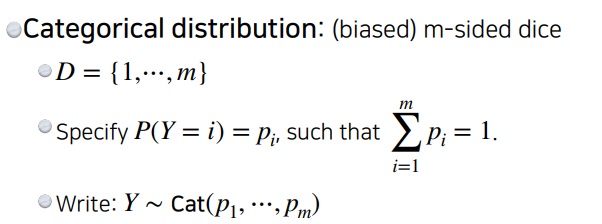
3. RGB 1 pixel modeling
RGB 1 pixel을 표현하기 위한 parameter의 수를 생각해보자.
확률모형 r,g,b ~ P(R,G,B)을 생각하자.
R,G,B 값은 각각 0~255중 하나의 값을 가진다.
각각이 가질 수 있는 경우의 수는 256가지이므로 총 나올 수 있는 경우의 수는 256*256*256= 16777216
그렇다면 Parameter의 수는?
위에서 구한 모든 경우의 수 각각에 확률을 부여하여 Categorical distribution으로 볼 수 있다.
즉, 수식으로 쓰면
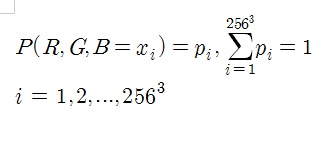
$256^{3} - 1 = 16777215$개의 확률만 결정하면 나머지는 자동적으로 결정되니까 필요한 모수의 수는 16777215개이다.
RGB 이미지의 겨우 1개의 pixel만 표현하려고 하는데도 필요한 parameter의 수가 어마어마하다는 것을 알 수 있다
추가로 R,G,B가 독립인줄 알았는데 이상한 생각이었네
R,G,B가 서로 독립적으로 0~255에서 하나의 값을 선택하여 1pixel의 색을 표현해야 자연스러운 생각이다.
그렇지 않다면, R,G의 색이 B의 색 결정에 영향을 미친다면 자연계에서 볼 수 없는 색이 나오지 않겠는가

4. 흑백이미지(binary image) n pixel modeling
흑백이미지를 구성하는 n개의 pixel X1 , X2 , ... ,Xn을 생각하자.
이들은 0아니면 1을 가지는 확률변수(Binary random variable)이다.
나타날 수 있는 모든 경우의 수는 Xi가 0,1의 2가지를 가질 수 있으므로 $2^{n}$
그렇다면 n pixel로 구성되는 흑백이미지 1장을 뽑아내는 확률분포 P(X1 , X2 , ... ,Xn)의 parameter의 수는?
먼저 각 픽셀이 독립이 아니라는 것이 중요하다.???
다시보니까 독립이 아닌가 독립이라해도 상관없는것 같기도하고
왜 독립이 아닌지는 너무나 명확한데 비슷한 위치에 있는 픽셀은 비슷한 값을 가져야 원하는 이미지를 표현할 수 있다.

예를 들어 숫자 9를 구성하는 주변 위치에서는 전부 0(이게 흰색인지 검정색인지는 모르겠지만)이라고 나와야 9를 표현할 수 있지 않겠는가
그러므로 이렇게 생각해야한다.
X1 , X2 , ... ,Xn이 가질 수 있는 모든 경우의 수 i=1,2,3,....,$2^{n}$ 각각에 대하여 확률을 부여한 categorical distribution을 생각하는 것이다.

$2^{n} - 1$개의 확률만 결정하면 나머지 1개는 자동적으로 결정되니까 필요한 모수의 수는 $2^{n}-1$개이다.
그렇게 커보이지 않은데 n이 충분히 크면 어떨까?
예를 들면 mnist data는 1장의 이미지가 28*28=784개의 pixel을 가지는데
필요한 모수의 수는 1000000000000000000000000000000000000………=약 $10^{236}$개로 어마어마하다
그래서 만약 n개의 pixel이 서로 독립이라고 가정해보자.
그러면 결합확률분포가 각각의 확률분포의 곱으로 표현되니까

P(Xi)는 Xi가 0아니면 1을 가지는 bernoulli variable이므로 1개의 모수만 있으면 된다.
그러므로 1을 n번 더하여 1+1+1+....+1 =n개만 있으면 표현할 수 있다.
$2^{n}-1$에서 n으로 줄었는데 그만큼 말이 안되는 강력한 가정이라는 것

'딥러닝 > 딥러닝 기초' 카테고리의 다른 글
| AI 모델 성능 평가 지표로 loss function은 왜 사용하지 않는가? (0) | 2025.04.19 |
|---|---|
| precision과 accuracy 개념 간단하게 (0) | 2024.08.21 |
| 현실에서 고려해야하는 모델 성능평가 지표 (0) | 2024.08.19 |
| backbone model이 필요한 이유 (0) | 2024.07.06 |
| L1 regularization vs. L2 regularization vs. elastic net 비교하기 (0) | 2024.06.17 |

