1. history
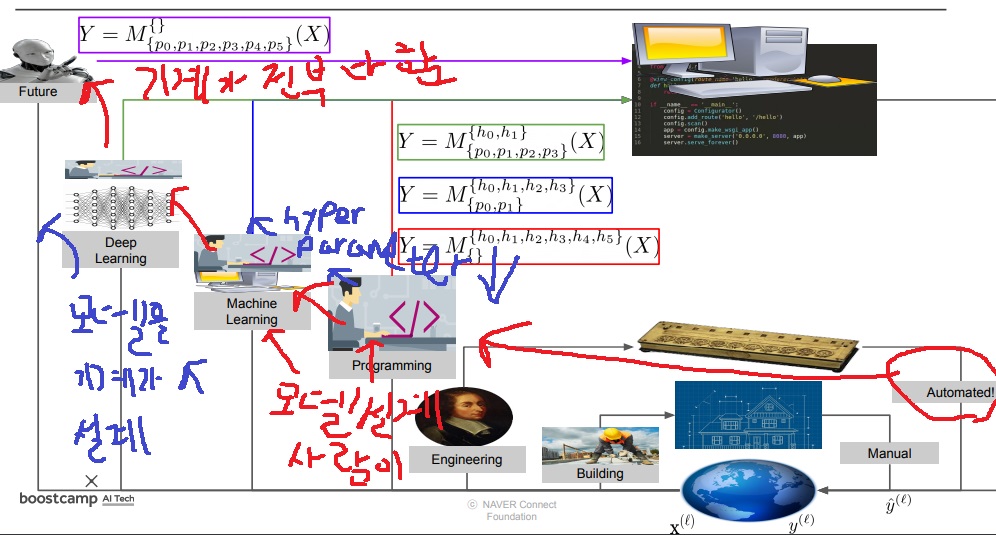
사람이 프로그래밍을 통해 모델을 설계하여 일을 자동으로 해주는 도구를 만들었지만
초기에는 hyperparameter밖에 없어서 사람이 모든 모수를 직접 정해야했다
머신러닝 시대로 오면서 데이터의 어떤 feature를 주로 쓸 지 모델 설계를 사람이 여전히 해야했지만
일부 parameter를 모델이 자동으로 찾아주었다. 물론 여전히 많은 hyperparameter가 존재했다.
딥러닝 시대로 오면서 사람이 input, output을 던져주면 모델이 알아서 feature를 잡아 모델을 설계했고
대부분의 parameter도 알아서 찾아준다. 극히 일부의 hyperparameter는 여전히 존재했다.
추후에는 진짜 모델 설계부터 parameter search까지 기계가 알아서 해주는 시대가 올 것이다.
2. data representation
1) vector space
좌표 공간 상의 vector로 표현하는 것이 보통
neural network는 vector space에 무작위로 섞여서 표현된 데이터를 구분하기 위해 decision boundary를 만들어 classification을 수행
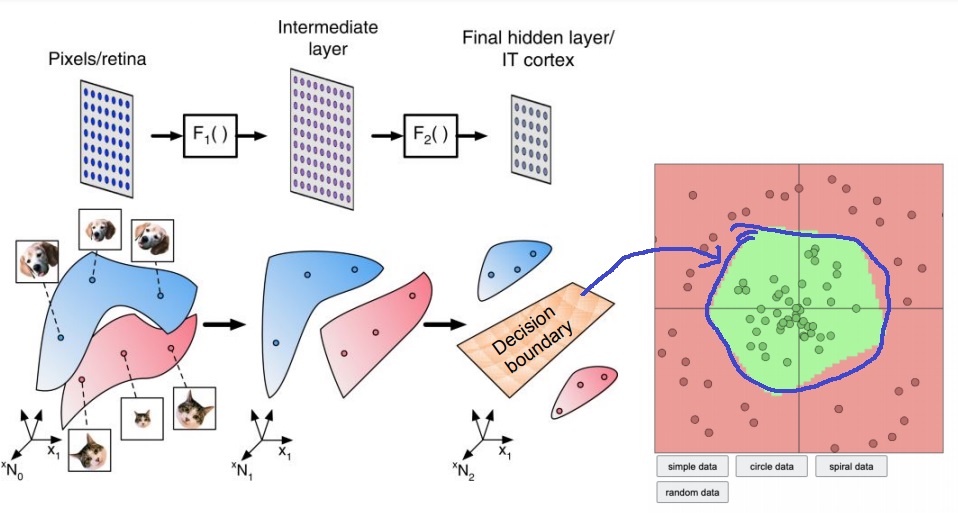
2) image map
RGB image map의 1 pixel은 3차원 공간에 표현될 것이지만 모든 pixel을 표현할려면 그 만큼 차원 수가 급격히 증가할 것

image map의 1pixel은 3차원에 표현 가능하지만 전체 map을 다 표현하려면 7*5*3차원에 표현해야함
3. binary search
정렬된 array를 반으로 나눠 원하는 값이 있는 array를 다음 array로 가져옴
다음 array에서 또 반으로 나눠 원하는 값이 있는 array를 가져옴
위 과정을 반복하면 원하는 값이 어디 있는지 찾을 수 있음
직선 상에서 optimal search
컴퓨터가 감당 못할 정도로 심각하게 array가 큰 것이 아니면 최적을 항상 찾을 수 있음
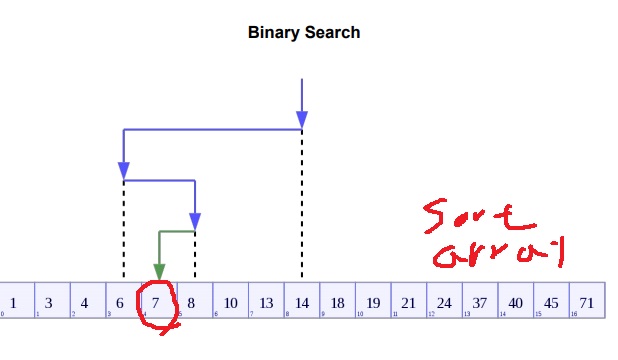
7을 찾고 싶은데 먼저 절반을 나눠 1~13까지 array를 가져오고
1~13에서 절반을 나눠 7,8,10,13을 가져오고
7,8,10,13에서 절반을 나눠 7,8을 가져오고 다시 절반을 나누면 7을 찾는다
4. gradient descent
다차원 공간상에서 optimal을 search하는 알고리즘
각 점에서 모델의 validation loss가 떨어지는 방향으로 다음 위치로 이동함
공간이 커질수록 objective를 정확히 나타내기 어려워서 어떤 local optimal에 빠질지 알 수 없다는 점
그래서 모든 경우를 찾지 않고 귀납적으로 optimal을 찾아나감
그래서 binary search와 결정적으로 다른 점은 optimal을 찾을 것을 기대는 하지만 항상 찾으리라는 보장이 없다는 것
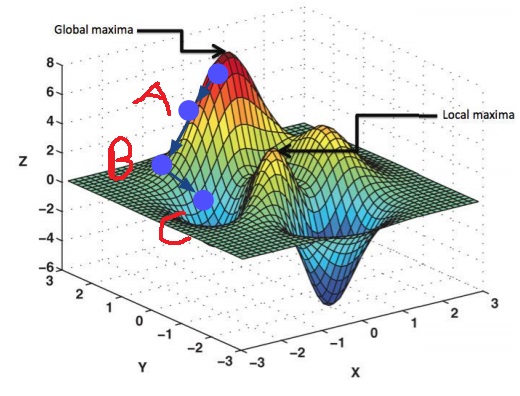
모든 경우를 검사하는 것이 아니고 순간 순간 validation loss가 떨어지는 방향을 찾기만 하면 그곳으로 이동하는 gradient descent
5. 머신러닝 모델의 기하학적 의미
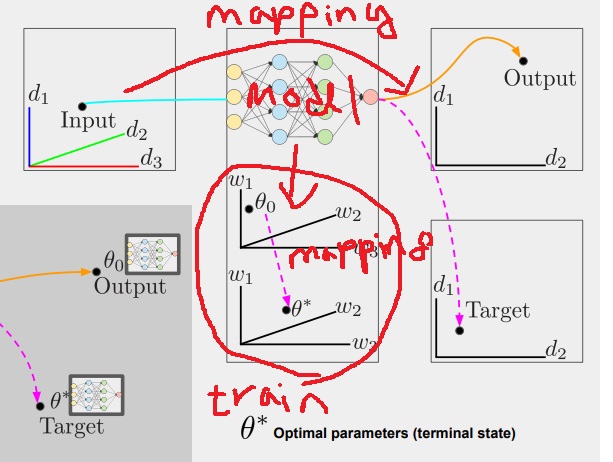
머신러닝 모델은 input data space를 output data space로 mapping시키는 transformation이다
개+고양이 이미지는 (RGB 3*pixel 수) <위의 예시에서 7*5*3>의 space 차원에 표현되는데 머신러닝에 투입되면 개 아니면 고양이가 되는데
개 아니면 고양이는 (1,0) , (0,1)의 2차원 one hot vector로 표현할 수 있다.
이 경우 머신러닝 모델은 7*5*3의 space의 데이터를 2차원 space로 mapping 시키는 역할을 하고 있다

6. optimization의 기하학적 의미
머신러닝 모델은 weight를 가지는데 weight도 다차원 공간상에 표현할 수 있다.
이런 머신러닝 모델을 train할 때 사용하는 optimization 과정에서 weight는 최적의 optimal weight로 이동하는데
이 역시 하나의 weight 공간을 다른 weight 공간으로 mapping 시키는 역할을 한다.
'딥러닝 > 딥러닝 기초' 카테고리의 다른 글
| backbone model이 필요한 이유 (0) | 2024.07.06 |
|---|---|
| L1 regularization vs. L2 regularization vs. elastic net 비교하기 (0) | 2024.06.17 |
| 결정을 기계에 맡기는 시대(deductive, inductive) (0) | 2024.05.09 |
| batch normalization 개념 간단하게 (0) | 2024.04.15 |
| hyperparameter 개념 간단하게 (0) | 2024.04.02 |

