1. 페리 수열의 길이
n번째 페리 수열은 분모가 n 이하인 0과 1 사이의 모든 기약분수를 오름차순으로 나열한 것이다.
기약분수가 무엇인가?
$\frac{a}{b}$가 기약분수라면 a와 b가 서로소라는 뜻이다.
이때, 0과 1 사이에 존재하는 기약분수이므로 a < b이다.
그러므로 n번째 페리수열에 존재하는 기약분수들은 다음과 같이 만들수도 있다.
"양 끝에는 $\frac{0}{1}, \frac{1}{1}$이 있고,
분모가 b = 2,3,4,5,..,n에 대하여 분자는 k보다 작으면서 서로소인 모든 정수 a에 대해 $\frac{a}{b}$를 나열한 것이다."
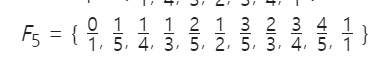
예를 들어, 5번째 페리 수열을 보자.
분모가 2이면 2와 서로소인 1에 대해 $\frac{1}{2}$
분모가 3이면 3과 서로소인 1,2에 대해 $\frac{1}{3}, \frac{2}{3}$
분모가 4이면 4와 서로소인 1,3에 대해 $\frac{1}{4}, \frac{3}{4}$
분모가 5이면 5와 서로소인 1,2,3,4에 대해 $\frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}$
이 때, n번째 페리수열은 n-1번째 페리수열에서 서로 이웃하는 두 기약분수 $\frac{a}{b} < \frac{c}{d}$에 대하여,
$\frac{a+c}{b+d}$를 생성한 것이라고 공부했다. 여기서 b+d <= n이다.
즉, n번째 페리수열은 n-1번째 페리수열을 모두 포함하고 있다.
n-1번째 페리수열이 만들어져있다고 생각해보자.
먼저 양 끝에 $\frac{0}{1}, \frac{1}{1}$을 만들고,
분모가 b = 2,3,4,...,n-1에 대하여, b보다 작으면서 서로소인 모든 정수 a에 대해 $\frac{a}{b}$를 만든것이다.
이 n-1번째 페리수열로부터 n번째 페리수열을 만들려고 한다면...
그냥 분모가 b = n에 대하여 n보다 작은 서로소인 모든 정수 a에 대해 $\frac{a}{n}$을 추가하면 된다.
따라서 n-1번째 페리수열에서 n보다 작은 서로소인 정수 개수만큼 길이가 증가한다.
n보다 작은 서로소인 정수의 개수는 오일러의 phi함수 $\varphi(n)$으로 구할 수 있다.
https://deepdata.tistory.com/571
오일러의 phi 함수 직접 구현해보면서 개념 익히기
1. 오일러의 phi 함수(Euler's phi function, totient function) $\varphi(n)$은 1부터 n까지의 자연수 중에서 n과 서로소인 자연수의 개수로 정의한다. 그 성질과 응용이 매우 다양하고 또 매우 어려운데... 하나
deepdata.tistory.com
그러므로 n번째 페리수열의 길이를 $|F_{n}|$이라고 하면,
$$|F_{n}| = |F_{n-1}| + \varphi(n)$$
2. 문제
11525번: Farey Sequence Length (acmicpc.net)
11525번: Farey Sequence Length
Given a positive integer, N, the sequence of all fractions a / b with (0 < a b), (1 < b N) and a and b relatively prime, listed in increasing order, is called the Farey Sequence of order N. For example, the Farey Sequence of order 6 is: 0/1, 1/6, 1
www.acmicpc.net
3. 풀이
말 그대로 n번째 페리수열의 길이를 구하는 문제
위에서 구한 점화식을 그대로 사용
다이나믹 프로그래밍을 이용해서 dp[1] = 2로 하고 dp[i] = dp[i-1] + phi(i)로 구할 수 있다.
from sys import stdin
def phi(n):
result = n
p = 2
while p*p <= n:
if n % p == 0:
while n % p == 0:
n = n//p
result -= result//p
p += 1
if n > 1:
result -= result//n
return result
dp = [0]*(10001)
dp[1] = 2
for i in range(2,10001):
dp[i] = dp[i-1] + phi(i)
p = int(stdin.readline())
for _ in range(p):
k,n = map(int,stdin.readline().split())
print(k,dp[n])
'정수론' 카테고리의 다른 글
| 페리 수열(farey sequence) 조금 더 깊게3 - 주어진 수의 다음 항을 찾는 방법 - (0) | 2024.02.07 |
|---|---|
| 페리 수열(farey sequence) 조금 더 깊게2 - 페리 수열의 대칭성과 페리 수열의 합 - (0) | 2024.02.07 |
| 페리 수열(Farey sequence) 문제를 해결하기 위해 알아야 할 기본 성질 간단하게 (0) | 2024.02.07 |
| 연분수(continued fraction)를 이용한 선형 디오판토스 방정식의 해를 구하는 방법 (0) | 2023.09.29 |
| 이항정리를 이용한 거듭제곱의 합 1^k+2^k+3^k+...+n^k 을 구하는 방법 (0) | 2023.08.26 |

