1. n번째 페리 수열
0부터 1사이의 분모가 n이하인 모든 기약분수를 오름차순으로 나열한 수열
n = 1부터 8까지의 경우를 나열하면 다음과 같다.

2. 두 분수 사이에 있는 분수
theorem1)
0과 1 사이의 두 분수 $\frac{a}{b}$와 $\frac{c}{d}$에 대하여 $\frac{a}{b} < \frac{c}{d}$라고 하자.
$$\frac{a}{b} < \frac{a+c}{b+d} < \frac{c}{d}$$이 항상 성립한다.
먼저 a,b,c,d가 자연수이므로 $\frac{a}{b} < \frac{c}{d}$에서 양변에 d를 곱하면
$\frac{ad}{b} < c$이고 다시 양변에 b를 곱하면 $ad < bc$이다.
그러므로 $bc - ad > 0$이다.
그런데 $$\frac{a+c}{b+d} - \frac{a}{b} = \frac{b(a+c) - a(b+d)}{b(b+d)} = \frac{bc-ad}{b(b+d)} > 0$$
마찬가지로 $$\frac{c}{d} - \frac{a+c}{b+d} = \frac{c(b+d) - d(a+c)}{d(b+d)} = \frac{bc-ad}{d(b+d)} > 0$$
따라서 두 분수 $\frac{a}{b} < \frac{c}{d}$이면, 단순하게 분자끼리 합하고 분모끼리 합하기만 하면..
두 분수 사이에 있는 분수 $\frac{a+c}{b+d}$를 얻는다.
3. n번째 페리수열에서 서로 이웃하는 두 기약분수
n번째 페리수열에서 두 분수가 서로 이웃하다는 것은 $\frac{a}{b}$와 $\frac{c}{d}$사이에 분수가 존재하지 않는 것이다.
예를 들어 4번째 페리수열에서 $\frac{1}{4}$와 $\frac{1}{3}$은 서로 이웃하는 두 기약분수이다.

두 기약분수 $\frac{a}{b}$와 $\frac{c}{d}$가 n번째 페리수열에서 서로 이웃하고 $\frac{a}{b} < \frac{c}{d}$라고 하자.
두 기약분수의 차이는.. $$\frac{c}{d} - \frac{a}{b} = \frac{bc - ad}{bd}$$
theorem2)
만약 n번째 페리수열에서 두 기약분수 $\frac{a}{b} < \frac{c}{d}$가 서로 이웃한 기약분수라면 bc-ad = 1이어야한다.
직관적으로는 bc-ad가 1보다 크다면 bc-ad보다 작은 k에 대하여 k/bd을 반드시 잡을 수 있고,
그러므로 a/b + k/bd인 기약분수가 a/b와 c/d사이 반드시 있기 때문이다.
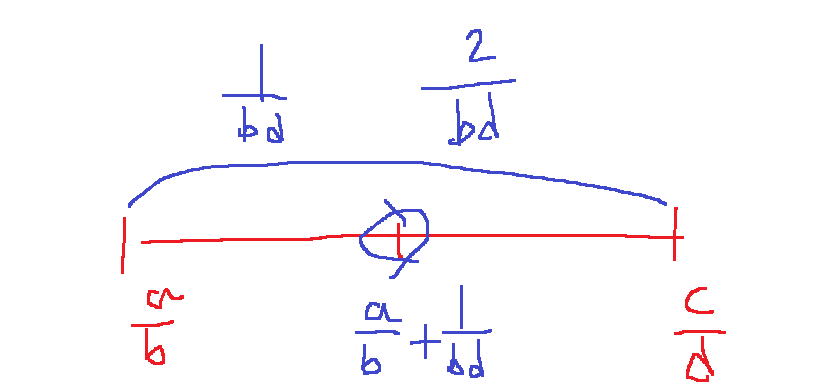
명확히는 수학적 귀납법으로 증명할 수 있다.
n = 1인 경우 서로 이웃하는 두 분수 0/1과 1/1은 a = 0, b = 1, c = 1, d = 1이므로 bc-ad = 1이다.

만약 n번째 페리수열에서 두 분수 $\frac{a}{b}$와 $\frac{c}{d}$가 이웃하면 bc-ad = 1이라고 하자.
그러면 n+1번째 페리수열에서 두 분수 $\frac{a}{b}$와 $\frac{c}{d}$가 서로 이웃할때, bc - ad = 1인지 보면 된다.
두 분수 사이에 있는 분수 $\frac{a}{b} < \frac{a+c}{b+d} < \frac{c}{d}$에 대하여, 2가지 경우가 있다.
먼저 b+d <= n+1이면 분모가 n+1이하이므로, n+1번째 페리수열은 다음과 같이
$$... ,\frac{a}{b}, \frac{a+c}{b+d}, \frac{c}{d}, ... $$가 존재한다.
이때 이웃하는 두 분수 $\frac{a}{b}$와 $\frac{a+c}{b+d}$를 보면 c = a+c, d = b+d이므로
bc - ad = b(a+c) - a(b+d) = ba+bc - ab-ad = bc - ad = 1이다.
마찬가지로 이웃하는 두 분수 $\frac{a+c}{b+d}$와 $\frac{c}{d}$를 보면 a = a+c, b = b+d이므로,
bc - ad = (b+d)c - (a+c)d = bc + cd - ad - cd = bc - ad = 1이다.
그런데 b+d > n+1이면, $\frac{a+c}{b+d}$는 분모가 n+1이하인 n+1번째 페리수열에 존재하지 않는다.
따라서 n+1번째 페리수열은 다음과 같이..
$$...., \frac{a}{b}, \frac{c}{d}, ...$$가 존재한다.
이때 이웃하는 두 분수 $\frac{a}{b}, \frac{c}{d}$는 가정에 의해 bc-ad = 1이다.
그러므로 어느 경우에나 n+1번째 페리수열에서도 이웃하는 두 분수에 대하여 bc - ad = 1이다.
따라서 모든 자연수 n = 1,2,3,..에 대하여 n번째 페리수열에서 이웃하는 두 분수 $\frac{a}{b}$와 $\frac{c}{d}$에 대해
bc - ad = 1이다.
---------------------------------------------------------------------------------------------------------------------------------------------------
4. bc - ad = 1이라는 조건
theorem3)
자연수 a,b,c,d에 대하여 bc - ad = 1이고 a < b, c < d이며 $\frac{a}{b} < \frac{c}{d}$라고 하자.
$\frac{a}{b}$와 $\frac{c}{d}$는 max(b,d)번째 페리수열의 이웃하는 두 기약분수이다.
b가 a의 배수로 b = ka라고 하자.
bc-ad = 1을 a로 나누면 kc - d = 1/a인데 좌변은 정수이고 우변은 유리수이므로 모순이다.
마찬가지로 d가 c의 배수이면 모순이다.
따라서 a,b는 서로소이고 c,d는 서로소이므로 a/b와 c/d는 0과 1 사이의 기약분수이다.
이 때 $\frac{a}{b}$와 $\frac{c}{d}$가 n = max(b,d)번째 서로 이웃하는 기약분수가 아니라면
$$\frac{a}{b} < \frac{p}{q} < \frac{c}{d}$$인 $\frac{p}{q}$가 존재한다.
$\frac{a}{b}$와 $\frac{p}{q}$의 차이와 $\frac{c}{d}$와 $\frac{p}{q}$의 차이는 0보다 커야한다.
$$\frac{bp - aq}{bq} > 0$$
$$\frac{cq - dp}{dq} > 0$$
따라서 bp - aq >= 1이고 cq - pd >= 1이다.
두 부등식에서 bp >= 1+aq, pd <= cq - 1
b,d는 자연수이므로 부등식을 각각 b,d로 나눠주면 p >= (1+aq)/b, p <= (cq-1)/d
따라서 (1+aq)/b <= p <= (cq-1)/d
그러면 우변과 좌변의 차이는 0이상이므로 (cq-1)/d - (1+aq)/b >= 0
(bcq - b) - (d+aqd) >= 0
bcq - b - d - aqd >= 0
q(bc-ad) - b - d >= 0
여기서 bc-ad = 1이므로 q >= b+d
그런데 n = max(b,d)이므로, b나 d중 하나는 n이고 다른 하나는 1이상의 자연수이므로 b+d는 무조건 n+1이상이다.
따라서 q >= b+d >= max(b,d)+1이다.
그러므로 $\frac{p}{q}$는 분모 q가 max(b,d)보다 크므로 max(b,d)번째 페리수열에 존재하지 않아서 모순이다.
따라서 bc - ad = 1이면 $\frac{a}{b} < \frac{c}{d}$는 max(b,d)번째 페리수열에서 서로 이웃하고 있다.
-------------------------------------------------------------------------------------------------------------------------------------
5. $\frac{a+c}{b+d}$의 성질
어떤 페리 수열에서 $\frac{p}{q}$가 $\frac{a}{b}$와 이웃하고, $\frac{c}{d}$와도 이웃하다고 하자.
즉, $\frac{a}{b} < \frac{p}{q} < \frac{c}{d}$이다.
페리 수열에서 서로 이웃하는 두 기약분수 사이에는 bc - ad = 1이라는 관계가 성립한다.
$\frac{a}{b}$와 $\frac{p}{q}$가 서로 이웃하므로 bp - aq = 1
$\frac{p}{q}$와 $\frac{c}{d}$가 서로 이웃하므로 cq - pd = 1
bp - aq = cq - pd
bp + pd = cq + aq
$$\frac{p}{q} = \frac{a+c}{b+d}$$
theorem4)
그러므로 n번째 페리수열에서 $\frac{a}{b} < \frac{c}{d}$이고 서로 이웃하지 않는다면,
n+1번째 페리수열에서 $\frac{a+c}{b+d}$가 유일하게 들어갈 수 있다.
이제 n번째 페리수열에서 서로 이웃하는 두 분수 $\frac{a}{b} < \frac{c}{d}$는 bc - ad = 1이다.
하지만 n+1번째 페리수열에서는 서로 이웃하지 않는다고 하자.
theorem5)
그럴때 들어갈 수 있는 두 분수 사이에 있는 분수 $\frac{a+c}{b+d}$는 반드시 기약분수이다.
$\frac{a+c}{b+d}$가 기약분수가 아니라고 가정해보자.
a+c와 b+d를 모두 나누어 떨어지게 하는 공통 소인수 p가 존재한다.
a+c = pq
b+d = pr
여기서 q,r은 서로소
첫번째 식의 양변에 b를 곱하고, 두번째 식의 양변에 a를 곱하면
ba + bc = bpq
ba + ad = apr
첫번째 식에서 두번째 식을 빼면 bc - ad = bpq - apr = p(bq - ar)
그런데 bc - ad = 1이므로 1을 나누는 소수 p는 존재하지 않는다.
따라서 $\frac{a+c}{b+d}$는 기약분수이다.
6. 페리 수열을 만드는 방법
위 결론들을 이용하면 다음과 같은 방법으로 페리 수열을 만들 수 있다.
먼저 1번째 페리수열은 $\frac{0}{1}$, $\frac{1}{1}$이다.
2번째 페리수열은 이 두 분수 사이에 $\frac{a+c}{b+d} = \frac{0+1}{1+1}$이 유일하게 들어갈 수 있다.
따라서 $\frac{0}{1}, \frac{1}{2}, \frac{1}{1}$이 2번째 페리수열이다.
3번째 페리수열은 $\frac{0}{1}, \frac{1}{2}$ 사이에 $\frac{0+1}{1+2} = \frac{1}{3}$이 유일하게 들어갈 수 있다.
그리고 $\frac{1}{2}, \frac{1}{1}$ 사이에 $\frac{1+1}{2+1} = \frac{2}{3}$이 유일하게 들어갈 수 있다.
따라서 $\frac{0}{1}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{1}{1}$이 3번째 페리수열이다.
4번째 페리수열도 비슷하게 구할 수 있다.
그런데 무조건 두 분수 사이에 분수를 생성할 수 있는 것은 아니다.
n번째 페리수열에서 분모가 n이하인 기약분수가 들어가야한다.
하지만 4번째 페리수열로부터 5번째 페리수열을 만들때, $\frac{1}{3}, \frac{1}{2}$ 사이에 $\frac{1+1}{3+2} = \frac{2}{5}$가 들어가야한다.
하지만 분모가 5인 기약분수이므로 4번째 페리수열에서는 들어가지 않는다.
그래서 $\frac{0}{1}, \frac{1}{1}$부터 시작해서 $\frac{a+c}{b+d}$를 중간에 넣는데, b+d <= n을 만족하면 넣어야한다.
이때 n번째 페리수열에서 서로 이웃하는 기약분수이므로 $\frac{a+c}{b+d}$는 따로 약분할 필요 없이 확실하게 기약분수이다.
#from sys import setrecursionlimit
#setrecursionlimit(100000)
def farey(a,b,c,d,n):
if b+d >= n+1:
sequence.append((c,d))
elif b+d <= n:
farey(a,b,a+c,b+d,n)
farey(a+c,b+d,c,d,n)
n = 4
sequence = [(0,1)]
farey(0,1,1,1,n)
print(sequence)
[(0, 1), (1, 4), (1, 3), (1, 2), (2, 3), (3, 4), (1, 1)]
'정수론' 카테고리의 다른 글
| 페리 수열(farey sequence) 조금 더 깊게2 - 페리 수열의 대칭성과 페리 수열의 합 - (0) | 2024.02.07 |
|---|---|
| 페리 수열(farey sequence) 조금 더 깊게1 - 페리 수열의 길이 - (0) | 2024.02.07 |
| 연분수(continued fraction)를 이용한 선형 디오판토스 방정식의 해를 구하는 방법 (0) | 2023.09.29 |
| 이항정리를 이용한 거듭제곱의 합 1^k+2^k+3^k+...+n^k 을 구하는 방법 (0) | 2023.08.26 |
| gcd와 xor의 성질, 연속하는 두 자연수는 서로소, dict보다 list를 먼저 고려하기 (0) | 2023.08.13 |

