1. introduction
target 변수를 예측하는데 얼마나 유용한지에 따라 feature에 적절한 점수를 할당하여 중요도를 측정함
model-specific한 방법은 머신러닝 모델 자체에서 feature importance를 계산하게 해주는 기능을 제공함
model-agnostic한 방법은 머신러닝 모델에서 제공하는 기능에 의존하지 않고 모델을 학습한 후에 적용되는 feature importance를 계산하는 방식
2. boosting tree model-specific feature importance
2-1) LightGBM
training된 LightGBM class에 feature_importance를 호출함
importance_type을 인자로 받는데 기본값은 'split'으로 tree 생성시 특정 feature가 몇번이나 split에 쓰였는지 횟수를 구함
fi[f'fold_{fold+1}'] = clf.feature_importance()
split에 많이 쓰였다는 것은 그만큼 중요한 feature라는 뜻
'gain'은 split하면서 해당 feature의 information gain이 총 얼마인지 계산함

2-2) XGBoost
training된 XGBoost class에 get_score함수를 호출함
feature_importance = np.array(clf.get_score().values())
fi[f'fold_{fold+1}'] = feature_importance
importance_type인자로 계산방식을 결정함
기본값은 ‘weight’로 LightGBM의 split과 동일함
‘gain’은 split하면서 feature의 information gain의 average값
‘total_gain’은 information gain의 총합
‘cover’은 average coverage를 계산해준다는데

leaf에서 분류된 training 데이터의 2차미분값의 총합?
leaf는 feature나 마찬가지니까.. 딱히 와닿지는 않는다
‘total_cover’은 coverage의 total값…
feature importance를 계산한 것을 보면 LightGBM과는 조금 다르다.. 모델 특성이 다르기 때문에 어떻게 보는지도 다르겠지

2-3) CatBoost
Training된 CatBoost class에서 get_feature_importance 함수를 호출하여 feature importance를 계산할 수 있음
fi[f'fold_{fold+1}'] = clf.get_feature_importance()
type으로 중요도 계산 방식을 설정할 수 있는데 CatBoost는 조금 특이하다..

다른 모델과 역시 feature importance 계산한 결과가 조금 다르다
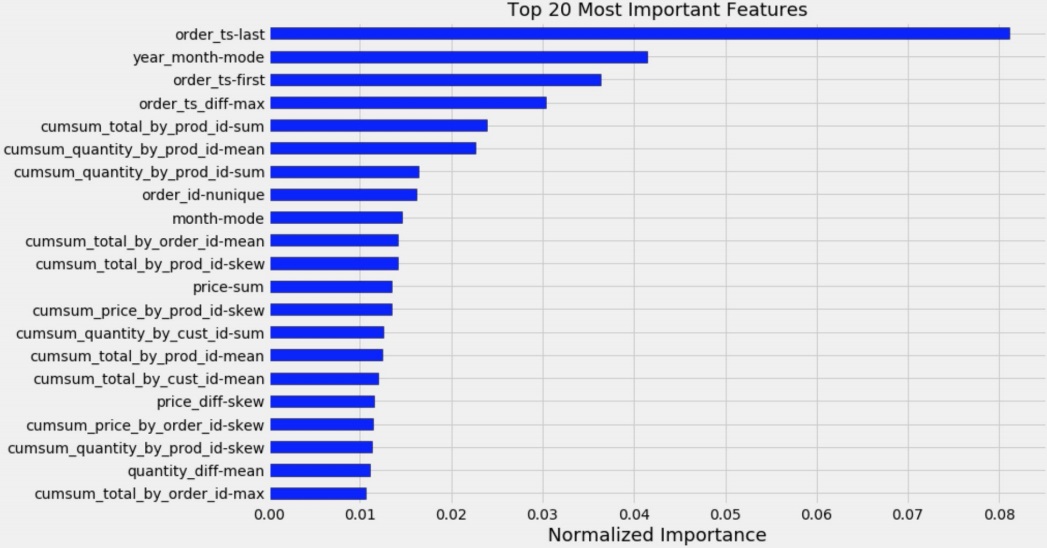
3. model-agnostic feature importance
3-1) permutation importance
feature의 값들을 random하게 shuffling하여 model의 error를 측정해봄
feature가 실제로 중요하다면 model은 prediction의 상당부분이 이 feature의 영향을 받으므로 feature값을 섞어버리면 model error가 상당히 커질 것임
중요하지 않다면 prediction에 별로 영향을 끼치지 않으므로 model error가 그닥 커지진 않을 것임
feature를 하나하나 순회하면서 데이터를 셔플링하여 model의 에러를 측정하여 섞지 않았을 때 비해 error가 얼마나 차이가 나는지 보고
차이가 클수록 그 feature는 중요하다고 보면 된다
모델 학습 후에 importance를 계산한다는 말의 의미를 이해할 수 있을 것 같다
요즘에 자주 쓰이고 마스터님 경험상 상당히 신뢰할만한 importance를 준다고함
tree model에서 제공해주는 model-specific은 참고용으로 쓰고 실제 feature 선택시에는 permutation을 많이 씀

trained model과 feature matrix와 target vector과 error function을 input으로 줌
미리 정의한 error function을 이용하여 현재 trained model의 error를 계산함
feature j개를 하나씩 순회하면서 해당 feature 번호에 대한 데이터를 permutation함
이러면 그 feature j와 true outcome 사이에 관계가 깨질거임
미리 정의한 error function으로부터 permutation된 데이터를 이용하여 error를 계산함
기존 error와 permutation된 데이터를 이용하여 계산한 error와의 차이를 계산
혹은 위의 설명보면 비율로도 계산할 수 있다고함
이렇게 계산한 error 차이를 크기순으로 정렬하면 error차이가 큰 값일수록 상당히 중요한 feature라는 것을 알려줌
sklearn에서 permutation_importance를 제공해준다
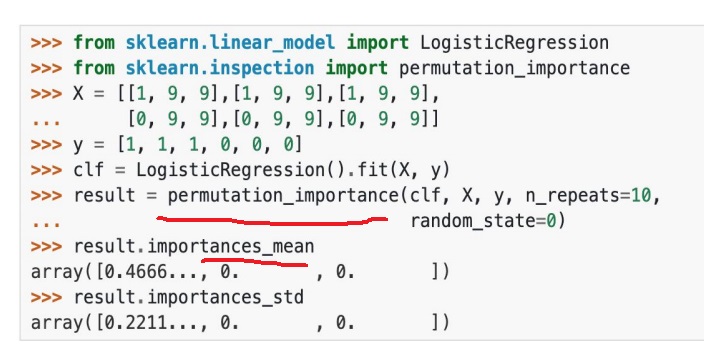
실제로 feature 각각을 단 1번만 shuffling해서 구한다면 random 효과때문에 우연히 중요한 변수가 error가 작을수도 있어서
여러번 shuffling해서 평균을 구해서 feature importance로 계산하나봄

앞서 말한 모델들이 본 중요도와는 조금 다르다는데 당연하겠지 뭐
이거 보면 중복 feature인데 중요도가 다르게 되어있는데 제거 안하는게 맞는것 같기도 하고??
'정형데이터' 카테고리의 다른 글
| 정형데이터를 위한 딥러닝 모델 TabNet 간단하게 (0) | 2024.08.25 |
|---|---|
| 정형데이터 분석에서 feature selection하는 몇가지 방법 (0) | 2024.04.03 |
| cross validation out of fold prediction (0) | 2023.12.07 |
| time series data의 cross validation에 대한 여러가지 고찰 (0) | 2022.06.28 |
| 데이터 전처리 - 이상치를 처리하는 방법의 기초 (0) | 2022.06.26 |

