담금질 기법(simulated annealing) 배우고 최소 외접원 문제(smallest enclosing circle problem) 풀기

1. 담금질 기법(simulated annealing)

 

담금질 기법은 인공지능에서 말하는 gradient descent와 비슷하다.

 

목적함수를 설정하고, 해당 함수를 최적화하는 해를 찾는 것이다.

 

현재 답의 근처 해를 적당히 찾은 다음, 해가 더 좋아질 경우에는 갱신하고 해가 좋아지지 않을 경우에는 확률적으로 갱신하는 기법이다.

 

다항시간에 해를 찾기 어렵다고 생각되면 적당히 좋은 해를 찾기 위해 사용되는 휴리스틱(heuristic) 방법이다.

 

마치 금속을 뜨거운 온도에 담금질하여 원하는 금속으로 만드는 과정과 비슷하다고 하여 이름 붙여진 듯 하다.

 

원하는 금속으로 만들려면 적절한 온도에 담그는게 중요한데, 담금질 기법의 핵심은 온도 설정에 있다.

 

인공지능의 gradient descent에서도 weight를 update할때, learning rate scheduler를 이용해서

 

learning rate를 바꿔가며 training할때 효과가 더 좋듯이, 담금질 기법도 마찬가지다.

 

초기에는 적절히 크게 탐색하면서 global optimal로 다가가지만, 어느 순간부터는 global optimal에 왔다고 생각한다면...

 

더욱 세밀하게 이동하면서 global optimal로 다가가야 local optimal로 빠지지 않을 것이다.

 

담금질 기법에서는 이를 매 시행마다 온도 감률을 곱하여 온도가 조금씩 감소한 상태로 시행하도록 구현한다.

 

보통 온도 감률은 0.95 ~ 0.9999정도의 실수를 사용한다고 한다.

 

2. 최소 외접원 문제(smallest enclosing circle problem)

 

13708번: 모든 점을 포함하는 원 (acmicpc.net)

13708번: 모든 점을 포함하는 원

 

2차원 평면 위에 점이 N개 주어질때, 이들을 모두 포함하는 가장 작은 반지름을 가진 원을 구하는 문제.

 

원의 둘레에 있어도 포함한다고 가정한다.

 

방법이야 여러가지 있지만 일단 가장 쉽다고 생각하는 담금질 기법으로 문제를 해결해보자

 

3. 풀이

 

주어진 점이 $(a_{1}, b_{1}), (a_{2}, b_{2}), ... , (a_{n}, b_{n})$이며 찾고자 하는 최소 외접원의 중심이 $(x,y)$라고 하자.

 

그렇다면 최소 외접원은 해당 모든 점을 포함하면서도 가장 작은 반지름을 가져야하므로,

 

중심부터 해당 점까지의 거리의 최댓값이 가장 작아야한다.

 

결국 다음과 같은 함수를 최소화 하는 x,y를 찾는 문제가 된다.

 

$$f(x,y) = max( ((x-a_{1})^{2} + (y-b_{1})^{2}) , ((x-a_{2})^{2} + (y-b_{2})^{2}), ... , ((x-a_{n})^{2} + (y-b_{n})^{2}) )$$

 

이 함수는 결국 $f = max(x_{1}^{2}, x_{2}^{2},...,x_{n}^{2})$과 같은 형태이다.

 

눈으로 확인해보기 위해 n = 2인 경우에 대해서 그려본다면 다음과 같은 형태라고 한다

 

 

 

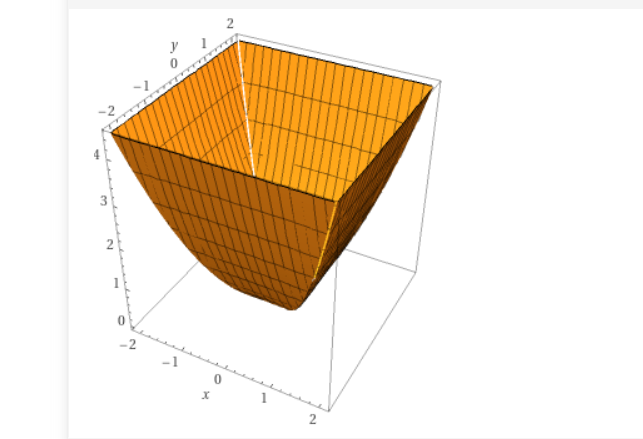
즉, global optimal만이 존재하는 함수이기 때문에 담금질 기법을 사용하면 반드시 global optimal에 도달할 수 있는 함수이다.

 

그러니까 휴리스틱한 방법으로도 정확한 정답을 찾을 수 있는 문제가 된다.

 

최초 시작 점은 모든 점의 좌표들의 평균으로 시작하자.

 

def simulated_annealing(x,y,n):
    
    X = sum(x)/n
    Y = sum(y)/n

 

근데 사실 시작점이 중요하진 않다. x[0], y[0]로 시작해도... 정답을 찾기는 한다

 

중요한건 온도와 시행횟수를 설정하는 건데... 초기 온도를 크게 설정하면 상대적으로 적은 횟수로 global optimal에 다가갈거고

 

초기 온도를 작게 설정하면 상대적으로 큰 횟수로 global optimal에 도달할 것이다.

 

그렇다고 너무 크게 설정하면 exploding이 일어나서 global에 못다가갈 위험이 있을거고..

 

너무 작게 설정하면 시간안에 통과를 못할거고..

 

이런걸 고려해서 적당한 값을 설정하고 확실히 정답을 찾고 싶으면 최대한 많은 epoch을 사용하는게 좋겠지

 

def simulated_annealing(x,y,n):
    
    X = sum(x)/n
    Y = sum(y)/n

    temperature = 0.2

    epochs = 50000

 

이제 매 epoch마다 정답인 (X,Y)와 모든 점 (x,y) 사이 거리를 조사해서, 최댓값을 찾는다

 

def simulated_annealing(x,y,n):
    
    X = sum(x)/n
    Y = sum(y)/n

    temperature = 0.2

    epochs = 50000

    for epoch in range(epochs):
        
        max_dist = 0

        max_ind = -1

        for j in range(n):
            
            dist = distance((X,Y),(x[j],y[j]))

            if max_dist < dist:
                
                max_dist = dist
                max_ind = j

 

다음 중심과의 거리가 최대인 점 x[max_ind], y[max_ind]을 찾았으면, X,Y를 정답에 더 가까운 값으로 갱신해야하는데..

 

처음에는 그냥 (X,Y)와 (x[max_ind], y[max_ind])를 이은 선분을 temperature 비율로 분할하는 점

 

X = x[max_ind]*temperature + X*(1-temperature)
Y = y[max_ind]*temperature + Y*(1-temperature)

 

으로 갱신했는데 정답을 찾기는 하더라고..

 

근데 너무 근본 없는것 같아서 gradient descent에서 갱신하듯이 갱신해보자고

 

기억이 안나면 잠깐 봐주고

 

https://deepdata.tistory.com/110

경사하강법 알고리즘(gradient descent algorithm)

 

$f(x,y) = (x - x[max_ind])^{2} + (y - y[max_ind])^{2}$가 될테니까, gradient를 구한다면...

 

각각을 x,y로 미분해서 (2(x-x[max_ind]), 2(y-y[max_ind]))가 될테니까..

 

X = X -temperature * 2*(X-x[max_ind]) 
Y = Y -temperature * 2*(Y-y[max_ind])

 

이렇게 갱신하고 나서, 가장 중요한 것은 temperature에 온도 감률을 곱해서 다음 시행에는 다른 온도로 바꿔줘야한다.

 

안바꾸면 틀릴 가능성이 매우 높아진다..

 

보통 0.95~0.9999를 사용한다니까 여기 사이에 적절한 값을 사용해보자

 

X = X -temperature * 2*(X-x[max_ind]) 
Y = Y -temperature * 2*(Y-y[max_ind])
temperature *= 0.9995

 

모든 시행이 끝나고 나서, 마지막에 구한 max_dist가 바로 중점과 가장 먼 점 사이 거리의 제곱이므로,

 

최소 외접원의 반지름의 제곱이다.

 

따라서, 이것의 제곱근의 2배를 return하면 된다

 

#담금질 기법을 이용한 최소 외접원 문제
from sys import stdin

#두 점 사이 거리
def distance(x,y):
    
    return (x[0]-y[0])**2 + (x[1] - y[1])**2

#담금질 기법
#f(x,y) = max((x-a1)^2+(y-b1)^2, ... , (x-an)^2+(y-bn)^2)을 최소화하는 x,y를 찾는 문제
#f = max(x^2,y^2)은 global optimal만 존재하는 함수
def simulated_annealing(x,y,n):
    
    #최소 외접원의 중점 초기값 설정
    X = sum(x)/n
    Y = sum(y)/n
    
    #global optimal을 찾을 수 있는 적절한 값을 설정해야함
    #temperature가 너무 크면 빠르게 global optimal로 다가가더라도, exploding 가능성이 있고
    #너무 작으면 굉장히 많은 시행횟수가 필요하다.
    temperature = 0.2 #온도(learning rate)
    
    #정확히 정답을 찾을려면 최대한 많은 시행횟수를 하는게 좋을 것이다
    epochs = 50000 #담금질 시행 횟수(epoch)
    
    #매 시행마다 모든 점들과 중점 (X,Y)사이 거리를 조사해서, 최댓값을 찾는다
    for epoch in range(epochs):
        
        max_dist = 0

        max_ind = -1

        for j in range(n):
            
            dist = distance((X,Y),(x[j],y[j]))

            if max_dist < dist:
                
                max_dist = dist
                max_ind = j
        
        #grdient descent방법에 의해 x < x - learning_rate*gradient로 갱신
        #혹은, (x[max_ind],y[max_ind])와 (X,Y) 사이 learning_rate 비율로 분할하는 점으로 갱신해도 답이 나오긴 한다
        #X = x[max_ind]*learning_rate + X*(1-learning_rate)
        #Y = y[max_ind]*learning_rate + Y*(1-learning_rate)
        
        X = X -temperature * 2*(X-x[max_ind]) 
        Y = Y -temperature * 2*(Y-y[max_ind])
        
        #온도 감률 0.95~0.9999사이 값중 하나를 매 시행마다 곱하여, 온도를 변화시키며 담금질 시행
        temperature *= 0.9995
    
    #마지막 시행에서 찾은 max_dist값이 최소 외접원의 반지름의 제곱이다 
    return 2*(max_dist**(1/2))
    
n = int(stdin.readline())

x = []
y = []

for _ in range(n):
    
    a,b = map(int,stdin.readline().split())
    
    x.append(a)
    y.append(b)

print(f'{simulated_annealing(x,y,n):.2f}')

 

 

https://ryute.tistory.com/35

PS: 뉴비를 위한 Simulated Annealing 입문 (1)

 

https://sens.tistory.com/404

Simulated Annealing, 담금질 기법

 

https://koosaga.com/3

동전뒤집기 ('06 KOI)와 Simulated Annealing (담금질 기법)