이분 매칭(Bipartite matching) 알고리즘 배우기

[그래프] Bipartite Matching

이분 매칭이란? 이전 글에서 Max-Flow를 구하는 방법에 대해 알아보았고, 마지막 부분에서는 문제 하나를 풀어보았습니다. icpc.me/11375 문제를 풀어보았고, 문제를 그래프로 모델링하면 아래 사진처

justicehui.github.io

29. 이분 매칭(Bipartite Match.. : 네이버블로그 (naver.com)

29. 이분 매칭(Bipartite Matching)

지난 번에 네트워크 플로우(Network Flow) 알고리즘에 대해 공부하는 시간을 가졌습니다. 이...

blog.naver.com

Kuhn's Algorithm - Maximum Bipartite Matching - Algorithms for Competitive Programming (cp-algorithms.com)

Kuhn's Algorithm - Maximum Bipartite Matching - Algorithms for Competitive Programming

Kuhn's Algorithm for Maximum Bipartite Matching Problem You are given a bipartite graph $G$ containing $n$ vertices and $m$ edges. Find the maximum matching, i.e., select as many edges as possible so that no selected edge shares a vertex with any other sel

cp-algorithms.com

1. 이분 그래프(bipartite graph)

정점을 두 그룹으로 나눌 수 있고, 각 그룹에 속하는 정점끼리는 간선으로 연결되어 있지 않은 그래프

https://deepdata.tistory.com/530

이분 그래프 판별하는 알고리즘 분석

1. 문제 그래프의 정점의 집합을 둘로 분할하는데 각 집합에 속하는 정점끼리는 서로 간선이 존재하지 않도록 분할하고 싶다. 이것이 가능한지를 판별하는 프로그램을 작성해본다면? 2. DFS 알고

deepdata.tistory.com

2. 이분 매칭(bipartite matching)

매칭(matching)은 이분 그래프에서 간선을 하나 선택하는 것이다.

간선을 선택한다는 것은 간선의 양 끝 정점도 선택하는 것이며.. 각 정점은 1번씩만 선택 가능하다.

이분 매칭 문제는 이분 그래프에서 최대의 매칭을 구하는 문제이다.

3. 예시로 이해하는 알고리즘

네트워크 플로우와 연관된 개념인것 같은데.. 이분 매칭은 매우 특수한 형태로 네트워크 플로우를 몰라도 풀 수 있는 방법이 있더라고

이 방법을 기본으로 이해하고 있으면 된다

다음과 같은 그래프를 생각해보자.

1번은 A,B를 원하고 2번은 A,C를 원하며 3번은 B,C,D,E를 원하고 4번은 A,B,E를 원하는 상황이다.

이런 상황에서 1,2,3,4번 각각이 A,B,C,D,E중 하나만을 선택할때, 서로 겹치지 않도록 최대의 매칭을 만들어주는 방법을 찾고 싶다.

먼저 1번 정점은 A,B에 매칭될 수 있으므로 일단 A번에 매칭시켜준다.

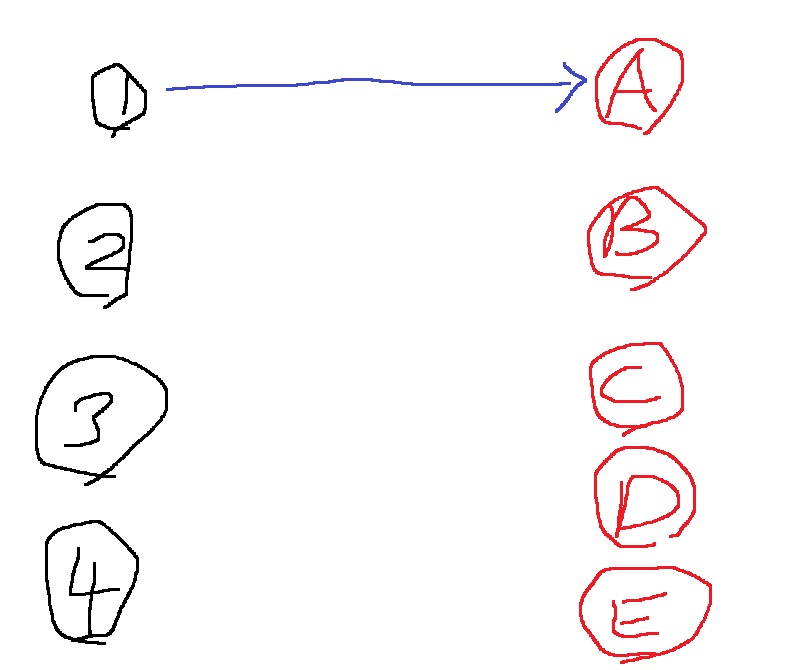
다음 2번을 매칭시켜줘야하는데, 2번이 A,C를 원하고 있다.

근데 A가 매칭이 되어 있기 때문에.. A에 매칭된 1번으로 다시 되돌아가서 1번을 다시 매칭시켜준다.

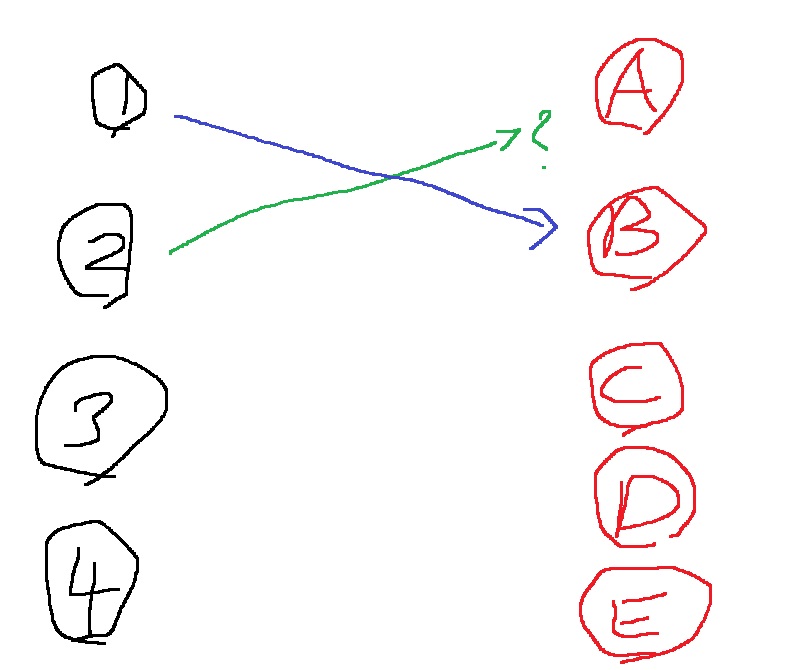
1번을 B에 연결시키는데 성공했으면, 2번 정점을 A번에 연결시켜준다.

다음 3번 정점을 매칭시켜야하는데 3번은 B,C,D,E를 원하고 있다.

그런데 B 정점이 1번과 매칭되어 있기 때문에 1번으로 다시 돌아가서 1번을 A,B 정점중 하나와 연결을 시도한다.

그런데 2번이 A번과 연결되어 있다. 그래서 다시 2번으로 되돌아간다.

이 때, 2번이 C번과 연결 가능하므로 C번과 연결 시키고, 다시 1번을 A번과 연결시키고, 3번을 B번과 연결시키면 된다.

이제 4번을 연결시켜야하는데, A,B,E를 원하고 있다.

4번을 방문체크하고 A번에 연결 시도하니, 방문체크 안한 1번이 연결되어 있어서 1번으로 다시 돌아간다.

1번을 방문체크하고 A,B에 연결시킬수 있는데 A를 연결 시도해보니 이미 방문 체크된 1번과 연결되어 있어서 넘어가고

B에 연결을 시도하는데 3번이 연결되어 있으니 아직 방문체크 안한 3번으로 들어가본다.

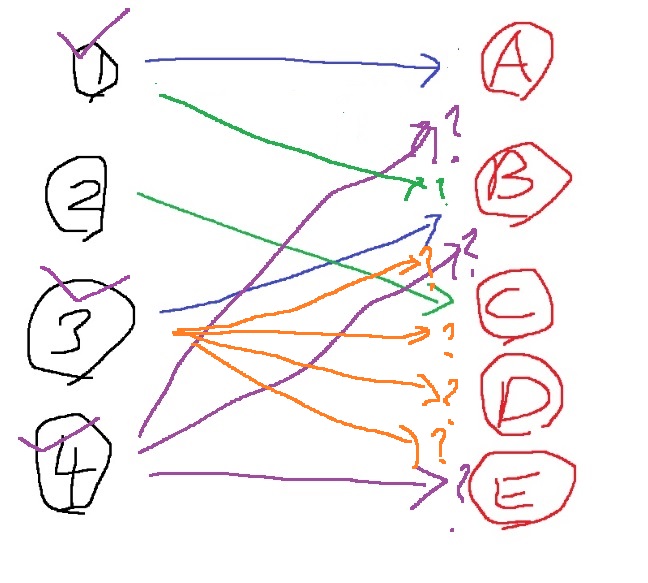
3번을 방문체크하고, 이 때 3번이 B,C,D,E에 연결시킬 수 있는데 B는 방문체크된 3번 자기 자신과 연결되어 있으니 넘어가고,

C번에 연결을 시도하는데 아직 방문체크 안한 2번과 연결되어 있으니 2번으로 들어가본다.

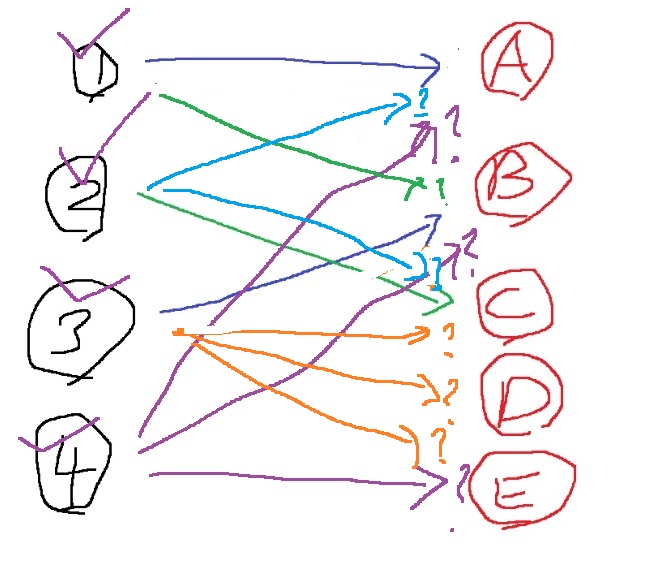
2번을 방문체크하고 2번은 A,C에 연결시킬 수 있는데 A에 연결된 1번에 대해서는 이미 체크해봤고,

C는 방문체크된 2번 자기 자신과 연결되어 있으니 넘어가고..

그러므로 1,2,3,4번이 모두 방문체크된 이 상태에서 더 이상의 이분 매칭은 불가능하다.

그러면 다음 상태로 되돌아온다.

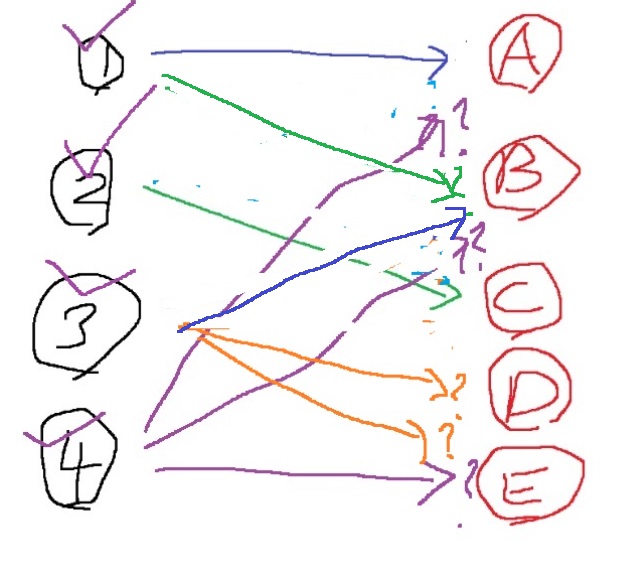
3번이 D,E에 연결을 시도 할 수 있는데 D에 연결을 시도해본다.

D는 아무것도 연결이 안되어 있으니 연결시킬 수 있고, B에 연결된 간선을 제거하고 D에 연결시켜주자.

그러면 1번을 B에 연결시킬 수 있게 된다. A에 연결된 간선을 제거하고 1번을 B에 연결시켜주자.

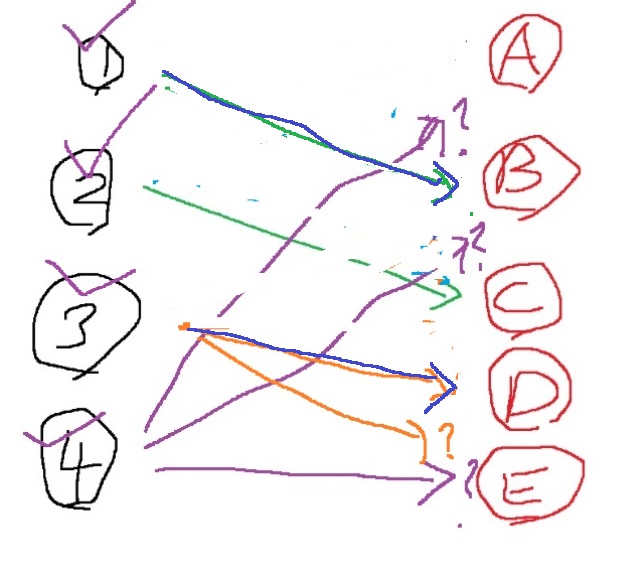
이제 A번 자리가 비게 되었다. 그러므로 4번을 A번에 연결시켜주자. 그러면 모든 매칭이 끝났다.

최종적으로 이분 매칭이 최대 4개 가능하게 된다.

4. 구현 예시

위 과정을 구현해보면 다음과 같다.

#DFS를 이용한 bipartite matching
#Kuhn's Algorithm
def bpm(s):
    
    #방문 체크한 s번에서 또 연결을 체크한다면...
    if visited[s] == 1:
        
        return False
    
    #최초로 s번에서 연결을 시도한다면.. 방문체크를 해주고
    visited[s] = 1
    
    #s와 연결된 모든 v에 대하여...
    for v in graph[s]:
        
        #v가 매칭되어 있지 않거나
        #v가 매칭되어 있다면, 해당 매칭된 번호 matching[v]로 다시 들어가서 연결을 재조정 
        if matching[v] == 0 or bpm(matching[v]):
            
            #매칭되어 있지 않거나, 연결을 재조정하는데 성공했다면 s를 v에 연결
            matching[v] = s

            #s번은 연결에 성공했으니 True
            return True
    
    #연결에 실패했다면...
    return False

#n: 왼쪽 그룹 정점의 수
#m: 오른쪽 그룹 정점의 수
n,m = map(int,input().split())

graph = [[] for _ in range(n+1)]

matching = [0]*(m+1) #오른쪽 그룹이 왼쪽의 어떤 정점들과 매칭되어있는지..

#1번부터 n번까지 정점 i에 대하여..
for i in range(1,n+1):
    
    #0번 원소는 i번과 연결된 정점의 수
    #1번 ~ 나머지 원소는 i번과 연결된 정점 번호
    lines = list(map(int,input().split())) 

    for j in range(1,lines[0]+1):
        
        graph[i].append(lines[j]) #i번 정점들이 어떤 정점들과 연결되어 있는지..

count = 0

#1번부터 n번까지 순회하여 매칭을 시도
for i in range(1,n+1):
    
    visited = [0]*(n+1)
    
    if bpm(i) == True:
        
        count += 1

print()
print(f'최대 매칭 수: {count}')
print()

change = {1:'A', 2:'B', 3:'C', 4:'D', 5:'E'}

for i in range(1,m+1):
    
    if matching[i] != 0:

        print(f'{matching[i]} -> {change[i]}')

4 5
2 1 2
2 1 3
4 2 3 4 5
3 1 2 5

최대 매칭 수: 4

4 -> A
1 -> B
2 -> C
3 -> D

5. 최적화1

약간의 테크닉으로 속도를 개선시킬 수 있는데, 의외로 다음 부분이 속도를 느리게 만든다.

왜 그럴까?

#s와 연결된 모든 v에 대하여...
for v in graph[s]:

    #v가 매칭되어 있지 않거나
    #v가 매칭되어 있다면, 해당 매칭된 번호 matching[v]로 다시 들어가서 연결을 재조정 
    if matching[v] == 0 or bpm(matching[v]):

        #매칭되어 있지 않거나, 연결을 재조정하는데 성공했다면 s를 v에 연결
        matching[v] = s

        #s번은 연결에 성공했으니 True
        return True

구체적으로 if 조건문이 문제인데

#v가 매칭되어 있지 않거나
#v가 매칭되어 있다면, 해당 매칭된 번호 matching[v]로 다시 들어가서 연결을 재조정 
if matching[v] == 0 or bpm(matching[v]):

우리는 위 알고리즘을 따라가본다면, matching[v] == 0이라면, bpm(matching[v])가 수행되지 않아도 된다는 것을 알 수 있다.

그러니까 s를 v에 연결을 시도하는데, v가 연결된 정점이 없다면 그냥 s를 v에 연결시키면 끝이다.

하지만 if matching[v] == 0 or bpm(matching[v]):라고 쓴다면,

matching[v] == 0이 참이더라도 파이썬은 bpm(matching[v])까지 수행해본다.

그래서 여기서 불필요한 시간이 소요된다.

왜냐하면 matching[v] == 0가 참인 순간 bpm(matching[v])가 False여야 전체 조건문이 거짓이기 때문

하지만 matching[v] == 0이 참이면 그냥 연결시키고 끝내길 원한다.

#DFS를 이용한 bipartite matching
#Kuhn's Algorithm
def bpm(s):
    
    #방문 체크한 s번에서 또 연결을 체크한다면...
    if visited[s] == 1:
        
        return False
    
    #최초로 s번에서 연결을 시도한다면.. 방문체크를 해주고
    visited[s] = 1
    
    #s와 연결된 모든 v에 대하여...
    for v in graph[s]:
        
        #v가 매칭되어 있지 않다면... s를 v에 매칭시키고 끝내버린다.
        if matching[v] == 0:
            
            matching[v] = s
            
            #s번이 연결에 성공했다면 True
            return True
    
    #s와 연결된 모든 v에 대하여...
    for v in graph[s]:
        
        #v가 매칭되어 있다면, 해당 매칭된 번호 matching[v]로 다시 들어가서 연결을 재조정 
        if bpm(matching[v]):
            
            #연결을 재조정하는데 성공했다면 s를 v에 연결
            matching[v] = s

            #s번은 연결에 성공했으니 True
            return True
    
    #연결에 실패했다면...
    return False

그러면 위와 같이 일단 첫번째 for문으로 s에 연결된 v를 모두 순회해서 matching[v] == 0인지만 조사하고,

그런 v가 존재한다면 연결시키고 True를 return해버리면 된다.

그런게 없다면 두번째 for문으로 s에 연결된 v를 순회해서, bpm(matching[v])로 연결을 재조정시킨다.

여기서 연결을 재조정하는데 성공했다면, s를 v에 연결시키고 True를 return한다.

이렇게 한다면 matching[v] == 0인데도 불구하고 bpm(matching[v])까지 수행하게 하는 비효율을 줄일 수 있다..

처음에는 이게 무슨 비효율적인 코딩이지? 생각했는데...

숏코딩이 무조건 좋은게 아니라는걸 보여주는 예시라고 해야할까?? 진짜 엄청나다...

실제로 시간이 절반으로 줄어든다..

6. 최적화2

cp-algorithms에서 제시한 방법인데... 처음에 matching 배열을 임의로 채우고 시작하는 것이다.

단순한 휴리스틱 알고리즘으로 임의의 매칭을 시킨다음에, 이분 매칭 알고리즘을 수행한다면, DFS 부담을 줄일 수 있다는 것

구체적으로 다음과 같이 수행할 수 있다.

n,m = map(int,input().split())

graph = [[] for _ in range(n+1)]

matching = [0]*(m+1)

for i in range(1,n+1):
    
    lines = list(map(int,input().split()))

    for j in range(1,lines[0]+1):
        
        graph[i].append(lines[j])

#arbitrary matching
#simple heuristic algorithm
random_visited = [0]*(n+1)

for i in range(1,n+1):
    
    for s in graph[i]:
        
        if matching[s] == 0:
            
            matching[s] = i
            random_visited[i] = 1
            break

#bipartite matching
count = 0

#1번부터 n번까지 매칭을 시도
for i in range(1,n+1):
    
    #i번에서 이미 위에서 수행한 랜덤매칭이 수행되어 있다면, 넘겨준다.
    if random_visited[i] == 1:
        continue
    
    #랜덤매칭이 되어있지 않다면, i번에 대해 bipartite matching을 시도
    visited = [0]*(n+1)
    bpm(i)

#matching배열을 모두 순회하여, 
#정점 번호는 1번부터 시작하니 matching[i]가 0이 아니면 매칭이 된 상태이다.
for i in range(1,m+1):
    
    if matching[i] != 0:
        
        count += 1
        
print(count)

실제로 위 최적화1을 쓰지 않고 최적화2만 쓴다면 시간이 절반으로 줄어들긴 한다..

근데 최적화1 + 최적화2 같이 쓰면 2배 효과가 있는건 아니다.

7. 연습문제

11375번: 열혈강호 (acmicpc.net)

11375번: 열혈강호

강호네 회사에는 직원이 N명이 있고, 해야할 일이 M개가 있다. 직원은 1번부터 N번까지 번호가 매겨져 있고, 일은 1번부터 M번까지 번호가 매겨져 있다. 각 직원은 한 개의 일만 할 수 있고, 각각

www.acmicpc.net

위 알고리즘 그대로 쓰면 정답

최적화 기법을 투입해서 구현하면 0.25초 정도

그냥하면 0.55초정도

'알고리즘 > 이분 매칭' 카테고리의 다른 글

이분 그래프 판별하는 알고리즘 분석 (0)	2022.11.05

TAGS.

통계학 세상

통계학 세상

통계학 세상