희소 배열(sparse table) 자료 구조 배우기

https://cp-algorithms.com/data_structures/sparse-table.html

Sparse Table - Algorithms for Competitive Programming

 

infossm.github.io/_posts/2019-03-27-fast-LCA-with-sparsetable.md at master · infossm/infossm.github.io

 

 

1. 개요

 

range query에 답을 하기 위한 자료 구조

 

대부분의 쿼리에 O(logN)에 답할 수 있지만, 진짜 파워는 range min,max query에 있다

 

O(NlogN)의 시간복잡도로 전처리하고, segment tree와는 다르게 업데이트가 불가능한 대신에 range min query에 O(1)에 답할 수 있다

 

 

2. 직관

 

모든 음이 아닌 정수는 감소하는 2의 거듭제곱 수열의 합으로 유일하게 표현할 수 있다.

 

(Any non-negative number can be uniquely represented as a sum of decreasing powers of two)

 

예를 들어 13 = 8 + 4 + 1이며, 정수 x에 대하여 최대 $\lceil log_{2}x \rceil$개의 합으로 표현된다.

 

비슷한 이유로, 구간도 길이가 2의 거듭제곱인 구간들의 합집합으로 유일하게 표현할 수 있다.

 

예를 들어 [2,14] = [2,9] + [10,13] + [14,14]이다. 

 

[2,14]의 길이는 14-2+1 = 13이고 [2,9] = 9-2+1 = 8, [10,13] = 13-10+1 = 4, [14,14] = 14-14+1 = 1

 

마찬가지로 구간의 길이가 x이면 최대 $\lceil log_{2}x \rceil$개 정도의 구간의 합으로 표현할 수 있다.

 

구간의 합집합이므로, [1,6] = [1,4] ∪ [3,6] 으로 표현할 수도 있다.

 

 

3. 전처리

 

2차원의 배열로 계산된 쿼리의 답을 저장할 것이다.

 

st[i][j]는 범위 길이가 $2^{i}$인 [j, j+$2^{i}$-1]의 답을 저장하게 된다.

 

구체적으로 range minimum query는 st[i][j] = min(A[j], A[j+1], ... , A[j+$2^{i}$-1])으로 j부터 연속한 $2^{i}$개의 원소들의 최솟값을 저장한다.

 

2차원 배열 st의 전체 사이즈는 (K+1) * (MAXN)이다. 

 

MAXN은 배열 길이를 나타낸다. 

 

K는 $K \geq \lfloor log_{2}MAXN \rfloor$을 만족시키는 정수 K로 선택한다.

 

왜냐하면 $2^{\lfloor log_{2}MAXN \rfloor}$이 범위의 가장 큰 경우이기 때문이다.

 

참고로 $MAXN = 10^{7}$개 정도의 원소에 대해 K=25가 적절하다.

 

 

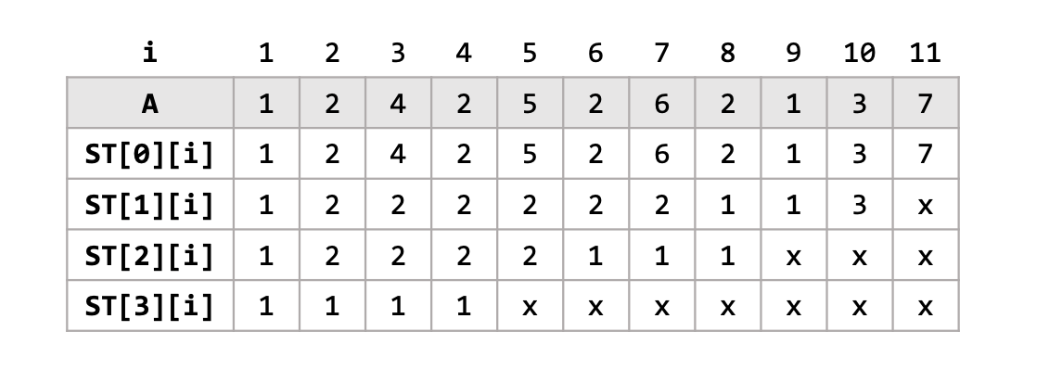
예를 들어 생각해보자.

 

A = [1,2,4,2,5,2,6,2,1,3,7]로 주어질때, ST[0][i]의 값은?

 

길이가 $2^{0} = 1$인 구간의 최솟값이므로.. 자기 자신들이 된다

 

i = 0이면, min(A[0],...,A[0+1-1]) = min(A[0]) = A[0]

 

...

 

i에 대하여 min(A[i], ... , A[i+1-1]) = min(A[i]) = A[i]

 

ST[0][i] = [1,2,4,2,5,6,2,1,3,7]

 

그러면 ST[1][i]의 값은? 길이가 $2^{1} = 2$인 구간의 최솟값

 

i = 0이면 min(A[0], A[1]) = 1

 

i = 1이면 min(A[1], A[2]) = 2

 

...

 

즉, min(A[i],A[i+1])의 값을 채워넣으면 [1,2,2,2,2,2,2,1,1,3,x]

 

여기서 A[11]은 존재하지 않으므로, ST[1][10]은 존재하지 않는다.

 

다음 ST[2][i]를 구한다면? 길이 $2^{2} = 4$인 구간의 최솟값들을 구한다.

 

즉, ST[2][i] = min(A[i],A[i+1],A[i+2],A[i+3])이 될 것이다. 

 

예를 들어 i = 0이면, min(A[0],A[1],A[2],A[3]) = min(1,2,4,2) = 1이다.

 

이런식으로 채워넣으면 ST[2][i] = [1,2,2,2,2,1,1,1,x,x,x]

 

A[11]부터는 존재하지 않으므로, i = 8부터는 정의되지 않는다.

 

n = 11이므로 k = 3정도가 적절하다.

 

그러므로 ST[3][i]까지 채워넣으면 되는데 길이가 8인 구간의 최솟값을 저장하면 된다

 

즉 ST[3][i] = min(A[i],A[i+1],A[i+2],...,A[i+7])

 

예를 들어 i = 0이면 min(1,2,4,2,5,2,6,2) = 1이다.

 

 

4. 전처리하는 방법

 

길이가 $2^{i}$인 구간 [j,j+$2^{i}$-1]은 2개의 구간 [j,j+$2^{i-1}$-1]과 [j+$2^{i-1}$,j+$2^{i}$-1]로 나눌 수 있다.

 

예를 들어 길이가 8인 [0,7]은 길이가 4인 2개의 구간 [0,3], [3,7]로 나눌 수 있다는 것이다. 

 

그러므로 다이나믹 프로그래밍을 이용하여 sparse table을 채워넣을 수 있다.

 

import math

n = 11
k = int(math.log2(n))

A = [1,2,4,2,5,2,6,2,1,3,7]

st = [[0]*(n) for _ in range(k+1)]

for i in range(n):
    
    st[0][i] = A[i]


for i in range(1,k+1):
    
    j = 0

    while j+(1<<i)-1 < n:
        
        #st[i][j] = [j,j+2^i-1] = [j,j+2^(i-1)-1] + [j+2^(i-1),j+2^i-1]

        #st[i-1][j] = [j,j+2^(i-1)-1] 

        #st[i-1][j+1<<(i-1)] = [j+2^(i-1),(j+2^(i-1))+2^(i-1)-1] = [j+2^(i-1), j+2^i-1]

        st[i][j] = min(st[i-1][j], st[i-1][j+(1<<(i-1))])

        j += 1

for row in st:
    
    print(row)

[1, 2, 4, 2, 5, 2, 6, 2, 1, 3, 7]
[1, 2, 2, 2, 2, 2, 2, 1, 1, 3, 0]
[1, 2, 2, 2, 2, 1, 1, 1, 0, 0, 0]
[1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0]

 

1) 점화식을 기억하는 방법은 st[i][j]가 [j,j+$2^{i}$-1]의 정답을 저장하는 것을 기억하자.

 

구간을 절반으로 나눈다면 [j,j+$2^{i}$-1] = [j,j+$2^{i-1}$-1] + [j+$2^{i-1}$, j+$2^{i}$-1]이다.

 

여기서 [j,j+$2^{i-1}$-1]은 j는 그대로이고 i 대신에 i-1을 넣은 st[i-1][j]가 된다.

 

$[j+2^{i-1}, j+2^{i}-1]$에서  $j+2^{i}-1 = j+2^{i-1} + 2^{i-1} - 1$이다. 

 

그러므로 j 대신에 $j + 2^{i-1}$을 넣고 i 대신에 i-1을 넣은 st[i-1][j + 2**(i-1)]이다.

 

 

2) 다이나믹 프로그래밍을 위해 i = 0은 A와 동일하므로 초기화하고, 

 

st[i][j]에서 j는 0~n-1이 들어가는데, j 부분에는 $j + 2^{i} - 1$이 들어가므로, j = 0부터 $j + 2^{i}-1$이 n-1일때까지 반복했다.

 

 

3) minimum range query를 가정했지만, 다른 쿼리에 대한 답을 하기 위해서 점화식 부분만 바꿔주면 될 것이다.

 

함수 f에 대한 쿼리의 답을 하고 싶다면..?

 

st[i][j] = f(st[i-1][j], st[i-1][j+(1<<(i-1))])

 

 

5. min 쿼리에 답을 하는 방법

 

sparse table을 어떻게 채워넣긴 했지만... 임의의 구간 [L,R]에 대한 답을 어떻게 찾아야할까?

 

위에서 보인대로, [L,R] 구간은 길이가 2의 거듭제곱인 여러개의 구간의 합으로 나눌 수 있음을 보였다.

 

예를 들어 길이가 6인 [1,6]은 길이가 4인 [1,4]와 길이가 4인 [3,6]의 합집합으로 구성할 수 있다.

 

여기서 주의할 점은 서로 독립인 구간이 아니라 [1,4]와 [3,6]은 부분집합 [3,4]가 있는데.. 상관 없다

 

분명히 min([1,6]) = min([1,4], [3,6])이기 때문이다. 왜냐하면 [1,4]와 [3,6]의 합집합이 [1,6]이기 때문이다.

 

즉, [L,R]은 길이가 i인 어떤 두 구간 [L, L+$2^{i}$ - 1]과 $[R - 2^{i} + 1, R-2^{i}+1  + 2^{i} - 1] = [R - 2^{i} + 1, R]$의 합집합으로 표현할 수 있다.

 

여기서 i 값은 [L,R]을 완전히 덮도록 분할시키는 값을 선택한다.

 

가장 무난한건 $i = log_{2}(R-L+1)$

 

그러므로, 임의의 구간 [L,R]의 답은 min(st[i][L], st[i][R-2**i+1])로 O(1)만에 답할 수 있다.

 

 

6. sum 쿼리에 답을 하는 방법

 

구간 [L,R]에 존재하는 모든 값들의 합을 구하고 싶다.

 

그러면 f 함수를 +로 고쳐서 sparse table을 구성할 수 있다.

 

st = [[0]*(n) for _ in range(k+1)]

for i in range(n):
    
    st[0][i] = A[i]


for i in range(1,k+1):
    
    j = 0

    while j+(1<<i)-1 < n:
        
        #st[i][j] = [j,j+2^i-1] = [j,j+2^(i-1)-1] + [j+2^(i-1),j+2^i-1]

        #st[i-1][j] = [j,j+2^(i-1)-1] 

        #st[i-1][j+1<<(i-1)] = [j+2^(i-1),(j+2^(i-1))+2^(i-1)-1] = [j+2^(i-1), j+2^i-1]

        st[i][j] = st[i-1][j] + st[i-1][j+(1<<(i-1))]

        j += 1

 

min query는 구간의 합집합으로 답을 구했지만, sum query는 단순히 구간의 합집합으로 답을 내면 중복되는 부분이 있어서 오답이다.

 

위에서 어떤 구간 [L,R]은 길이가 2의 거듭제곱으로 감소하는 수열의 구간 합으로 나타낼 수 있음을 보였다.

 

즉 길이가 13인 구간을 길이가 8,4,1인 구간의 합으로 나타냈다.

 

[2,14] = [2,9] + [10,13] + [14,14]

 

그러므로 i = k부터 i = 0까지 길이가 $2^{i}$인 구간 [L,L+$2^{i}$-1]의 정답 st[i][L]을 누적합하면 된다.

 

그런 다음에 더해줄 구간은 st[i][L+$2^{i}$]이다.

 

왜냐하면 [L,R] = [L,L+$2^{i}$-1] + [L + $2^{i}, L+2^{i+1}-1] + ... + [...,R]으로 구간 간격이$2^{i}$씩이기 때문이다.

 

[2,9]는 길이가 8이고, 다음 구간은 8을 점프한 2+8 = 10부터 시작하고, i = 3에서 1 감소한 i = 2의 길이 $2^{i} = 4$의 구간 [10,13]을 더해준다.

 

마찬가지로 다음은 10+4 = 14로 점프하고, 길이는 i = 2에서 1 감소한 i = 1의 길이 $2^{i} = 2$의 구간 [14,15]를 더하는데...

 

15가 최대 길이 [2,14]를 넘어가므로 여기는 더하지 않는다.

 

현재 l = 14이고 r = 14인데, r-l+1 = 1이고, 1<<i = 2여서 1 << i가 1보다 크므로 더하지 않는다.

 

다음 i = 0으로 감소시키고 길이 $2^{i} = 1$의 구간 [14,14]를 더한다. 

 

for i in range(k,-1,-1):
    
    if ((1<<i) <= r-l+1):
        
        sum += st[i][l]
        l += (1 << i)

 

min query와는 다르게 i = k부터 0까지 순회하므로, O(K) = O(logN)의 시간 복잡도를 요구한다.

 

대부분의 함수에 대한 쿼리는 이 정도 시간 복잡도를 요구하게 된다.

 

7. 연습문제 1

 

10868번: 최솟값 (acmicpc.net)

10868번: 최솟값

 

업데이트가 없는 배열에서 최솟값 쿼리들에 답을 하는 문제

 

업데이트가 없으면서 최솟값을 구하는 쿼리이므로, 희소 배열을 사용하기에 매우 적절하다.

 

import math
from sys import stdin

#sparse table, range min query basic

def sparse_table(A):
    
    k = int(math.log2(n))
    
    #st[i][j] = 구간 [j, j+2^i-1]에 대한 정답
    st = [[0]*n for _ in range(k+1)]
    
    #i = 0인 경우는 원래 배열 A와 동일하다.
    for i in range(n):
    
        st[0][i] = A[i]
    
    #구간의 길이를 절반으로 나눠서, 이전에 구한 답들을 이용하여
    #다이나믹 프로그래밍을 이용해 sparse table을 채워넣는다.
    for i in range(1,k+1):
    
        j = 0

        while j + (1 << i) - 1 < n:
        
        #st[i][j] = [j,j+2^i-1] = [j,j+2^(i-1)-1] + [j+2^(i-1),j+2^i-1]

        #st[i-1][j] = [j,j+2^(i-1)-1] 

        #st[i-1][j+1<<(i-1)] = [j+2^(i-1),(j+2^(i-1))+2^(i-1)-1] = [j+2^(i-1), j+2^i-1]
        
            st[i][j] = min(st[i-1][j], st[i-1][j+(1<<(i-1))])

            j += 1
    
    return st

#range min query에 답을 하는 방법

#[l,r]에서 최솟값 min([l,r])은 어떤 길이 2^i인 두 구간 
#min([l,l+2^i-1], [r-2^i+1,r])에서 최솟값과 동일하다.

#i = log2(r-l+1)

def min_query(a,b):
    
    k = int(math.log2((b - a + 1)))
    
    return min(st[k][a-1],st[k][b-1-(1<<k)+1])
    
n,m = map(int,stdin.readline().split())

A = [int(stdin.readline()) for _ in range(n)]

st = sparse_table(A)

for _ in range(m):
    
    a,b = map(int,stdin.readline().split())
    
    print(min_query(a,b))