1. 문제
27965번: N결수
$10$진법 상에서 양의 정수 $1$, $2$, $3$, $\cdots$, $N$을 이어 붙여 만든 수 $\overline{123\cdots N}$을 $N$결수라고 한다. 예를 들어 $12345$는 $5$결수이고, $12345678910111213$은 $13$결수이다. $N$과 정수 $K$가 주어
www.acmicpc.net
2. 풀이1
쉽다는데... 솔직히 까다로운 문제같다
n이 10의 7제곱까지라 n결수를 만들면 당연히 시간초과일거고 (애초에 만들어지지도 않음)
그 전에 근본적으로 나눗셈 연산을 어떻게 하는지 생각을 해보면..
1234를 5로 나누는 것은 어떻게 할까?
1을 5로 나눠보고.. 몫이 0이고 나머지가 1이니까 아래로 1을 내려준다..
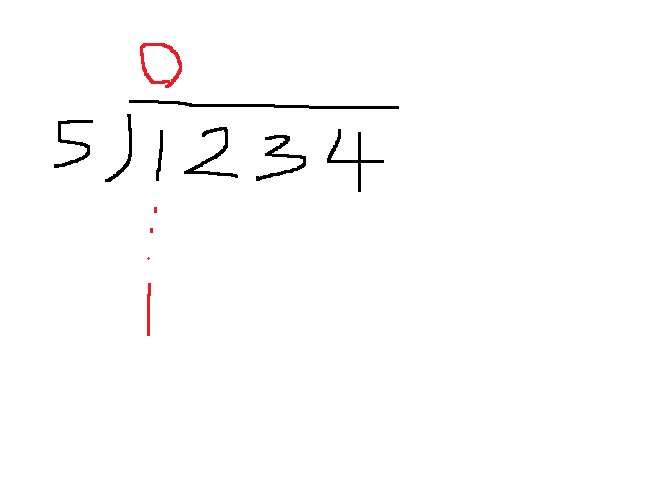
그리고 다음 내려온 1에 2를 붙여서.. 12를 5로 나눠본다
그러면 몫이 2이고 나머지가 2니까..

다시 다음은 3을 2에 붙여서... 23을 5로 나눠본다
그러면 몫이 4이고 나머지가 3이니까..

마지막 남은 4를 나머지 3에 붙여서.. 34를 5로 나눠본다
그러면 나머지가 4니까.. 결국에 1234를 5로 나눈 몫은 246이고 나머지는 4이다

여기까지 복기해보니 예시가 좋지 않았다는 생각이 든다..
아무튼 위 과정을 생각해보면 n결수를 안만들고도 n결수를 k로 나눈 나머지를 구할 수 있겠다는 생각이 든다
1부터 n까지를 차례대로 붙인 수를 n결수라고 정의한다면..
1부터 n까지 차례대로 순회해서.. 그 수를 i라고 한다면..
i를 k로 나눈 나머지가 r이면 r을 어떤 변수에 저장하고
다음 i를 r의 옆에 붙인 다음에 그 붙인 수를 다시 k로 나눈 나머지를 새로운 변수에 저장하고..
다시 다음 i를 옆에 붙인 다음 k로 나눈 나머지를 새로운 변수에 저장하고.. 이를 계속 반복한다면..
그것이 어떤 수를 k로 나눈 나머지를 구하는 과정이 아닌가?
어렵게 생각할 것 없이.. 그냥 나눗셈을 하는 과정을 그대로 구현하면 된다
from sys import stdin
n,k = map(int,stdin.readline().split())
div = ''
for i in range(1,n+1):
div += str(i)
z = int(div) % k
div = str(z)
print(int(div) % k)
3. 조금 최적화
풀이가 상당히 하수다..
알고리즘의 핵심에 잘 접근했지만.. 문자열 덧셈을 한다든지 정수를 문자열로 바꾼다든지..
이게 k가 10의 9제곱이다보니 최악의 경우 시간복잡도가 커질수 있다
문자열 연산을 안하는 방법이 없을까?
구체적으로 어떤 수 a 옆에 b를 문자열 연산을 안하고 붙이는 방법이 있을까?
사실 예전에 문제 풀어보면서 익히긴했다..
a에 10을 곱하고 b를 더하면 된다!!
예를 들어 2에 3을 붙여 23을 만들고 싶으면.. 2에 10을 곱해 20을 만들고 여기에 3을 더하면 되잖아
근데 이는 b가 한자리라 해당되는 얘기고
예를 들어 3에 12를 붙여서 312를 만들고 싶은데 3에 10을 곱해 30을 하고 12를 더하면 42가 되잖아
이럴때는 3에 100을 곱해 300을 만들고 여기에 12를 더해 312를 만들어야겠지
더 구체적으로는.. a에 b의 자리수만큼 10의 거듭제곱을 한 값을 곱하고, b를 더해야 a와 b를 붙일 수 있겠지
-----------------------------------------------------------------
다음 b의 자리수는 어떻게 구할까?
얼핏 기억에 팩토리얼 문제 풀면서 배운것 같다..
https://deepdata.tistory.com/605
팩토리얼(factorial)의 비밀 - 스털링 근사 공식과 자리수 계산하기
1. 팩토리얼의 자리수 $$n! = 1\times2\times...\times n$$로 계산된다. 어떤 정수에 1~9까지 중 하나를 곱하면 자리수가 늘어날수도 있지만, 늘어나지 않을수도 있다 하지만 10 이상을 곱하면 최소한 1자리
deepdata.tistory.com
$log_{10} b + 1$을 하면 된다..
따라서.. 문자열 연산도 안하고 n결수를 만들지 않고도 n결수를 k로 나눈 나머지를 구하는 방법은..
from sys import stdin
import math
n,k = map(int,stdin.readline().split())
div = 1
for i in range(2,n+1):
div *= (10**(int(math.log10(i))+1))
div += i
div %= k
print(div % k)
'정수론' 카테고리의 다른 글
| 피보나치 수열 심화과정2 - 자연수 n이 피보나치 수인지 바로 알 수 있을까? - (0) | 2023.05.23 |
|---|---|
| 피보나치 수열 심화과정1 - n번째 피보나치 수를 바로 계산할 수 있을까? (피보나치 수열의 일반항과 황금비)- (0) | 2023.05.22 |
| 밀러 라빈 소수 판별법(Miller-Rabin primality test) 배우기 (0) | 2023.05.05 |
| 1부터 n까지의 최소공배수를 빠르게 구하는 방법 (0) | 2023.05.04 |
| 세 수의 최소 공배수를 최대로 만드는 방법 (0) | 2023.04.27 |

