파이썬 실수 오차 없이 정확하게 계산하게 해주는 Decimal

1. 문제

 

12727번: Numbers (Small) (acmicpc.net)

12727번: Numbers (Small)

 

2. 풀이

 

문제 자체는 상당히 간단하다

 

$(3+\sqrt{5})^{n}$의 정수부분 뒤에서 3자리까지를 정확하게 구하라

 

여기서 n은 2부터 30까지이다.

 

그러니까 n은 2부터 30까지 미리 구해놓고, 테스트케이스에 대응하면 될 것이다

 

근데 막상 해보면 간단하지가 않다..

 

$\sqrt{5}$가 실수라, n이 커질수록 오차가 생긴다

 

이는 컴퓨터가 실수를 2진수로 저장해서 그렇다. 만약 10진수 형태로 산술연산을 할 수 있다면 오차가 생기지 않을 것이다.

 

이를 도와주는 파이썬의 모듈이 decimal의 Decimal 객체이다.

 

decimal — 십진 고정 소수점 및 부동 소수점 산술 — Python 3.11.3 문서

decimal — Decimal fixed point and floating point arithmetic

 

• Decimal “is based on a floating-point model which was designed with people in mind, and necessarily has a paramount guiding principle – computers must provide an arithmetic that works in the same way as the arithmetic that people learn at school.” – excerpt from the decimal arithmetic specification.

 

"컴퓨터는 사람이 학교에서 배운 산술 연산 방식과 동일한 방식으로 작동하는 산술 연산을 제공해야한다는 원리에 입각하여 만들어진 floating-point model"

 

파이썬 소수 연산 - float 타입과 decimal 모듈 | Engineering Blog by Dale Seo

파이썬 소수 연산 - float 타입과 decimal 모듈

 

019 소수점을 정확하게 계산하려면? ― decimal.Decimal - 점프 투 파이썬 - 라이브러리 예제 편 (wikidocs.net)

019 소수점을 정확하게 계산하려면? ― decimal.Decimal

 

 

Decimal은 실수 연산을 우리가 아는 10진수 연산으로 정확하게 해준다

 

Decimal을 쓸때는 문자열 형태로 넣어줘야 한다.

 

1.1이라는 값을 정확하게 1.1로 나타내고 싶다면...

 

 

 

 

먼저 $(3+\sqrt{5})$가 계산해보니 5.23606797749979래

 

 

그래서 다이나믹 프로그래밍?방식으로 30승까지 Decimal을 이용해서 다음과 같이 구해봄

 

from decimal import *

A = [0]*31

A[1] = Decimal('5.23606797749979')

for i in range(2,31):
    
    A[i] = A[i-1]*A[1]

A

 

대충 이런 느낌으로 결과가 나오는데

 

 

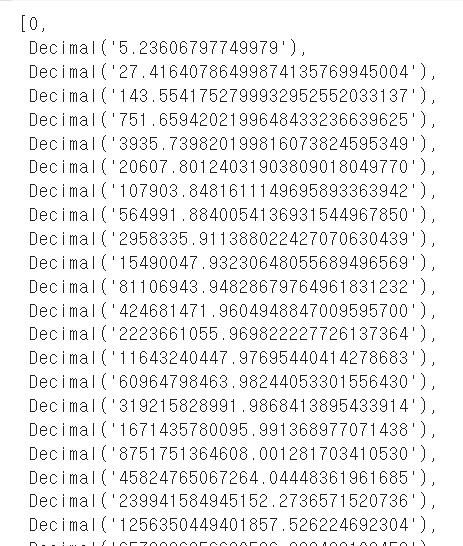
그러면 int()를 씌우면 정수부분만 가지고오더라고..?

 

그래서 int()를 씌워서 정수부분만 가지고 온 다음에... 1000으로 나눠주면 정수부분에서 뒤에서 3자리만 가지고올거다

 

이때, 3자리가 안된다면, 앞에 0을 붙여야하니까 str()로 바꿔주자고

 

from decimal import *

A = [0]*31

A[1] = Decimal('5.23606797749979')

B = [0]*31

B[1] = str(int(A[1])%1000)

while len(B[1]) != 3:
    
    B[1] = '0' + B[1]

for i in range(2,31):
    
    A[i] = A[i-1]*A[1]

    B[i] = str(int(A[i])%1000)

    while len(B[i]) != 3:
        
        B[i] = '0' + B[i]

B

 

이렇게 계산하면...

 

[0,
 '005',
 '027',
 '143',
 '751',
 '935',
 '607',
 '903',
 '991',
 '335',
 '047',
 '943',
 '471',
 '055',
 '447',
 '463',
 '991',
 '095',
 '608',
 '264',
 '152',
 '857',
 '536',
 '789',
 '602',
 '504',
 '862',
 '435',
 '876',
 '668',
 '564']

 

위와 같이 나와서..  해보면 오답임

 

왜 오답인지 보면.. 아래 그림에 답이 있다

 

 

n이 커질수록 소수점 이하 자리수가 줄어드는거 볼 수 있다

 

그러니 누적오차가 커지면서, 정수부분이 부정확해질 것이다

 

그러면.. 이번엔 Decimal(3+5**(1/2))로 실수를 Decimal()에 그대로 넣어서 계산을 해봄

 

from decimal import *

A = [0]*31

A[1] = Decimal(3+5**(1/2))

B = [0]*31

B[1] = str(int(A[1])%1000)

while len(B[1]) != 3:
    
    B[1] = '0' + B[1]

for i in range(2,31):
    
    A[i] = A[i-1]*A[1]

    B[i] = str(int(A[i])%1000)

    while len(B[i]) != 3:
        
        B[i] = '0' + B[i]

B

 

이렇게 해서 사용해보면 오답

 

[0,
 '005',
 '027',
 '143',
 '751',
 '935',
 '607',
 '903',
 '991',
 '335',
 '047',
 '943',
 '471',
 '055',
 '447',
 '463',
 '991',
 '095',
 '607',
 '264',
 '152',
 '856',
 '531',
 '760',
 '441',
 '625',
 '075',
 '408',
 '550',
 '250',
 '167']

 

그러면 이번엔... $(3+\sqrt{5})$를 Decimal()을 이용해서 그대로 계산해보자

 

Decimal(a).sqrt()는 a의 제곱근을 완전한 정밀도로 구해준다네

 

 

그리고 Decimal()은 그 자체로 산술연산이 가능

 

앞에서 쓴거랑 비슷해보이는데..?

 

그래서 비교해봄

 

 

그러면 왠지 3번째가 정확하게 계산을 해주는 것 일것 같다

 

이렇게 계산해보면 실제로 정답이다

 

from sys import stdin

T = int(stdin.readline())

compute = [0,
 '005',
 '027',
 '143',
 '751',
 '935',
 '607',
 '903',
 '991',
 '335',
 '047',
 '943',
 '471',
 '055',
 '447',
 '463',
 '991',
 '095',
 '607',
 '263',
 '151',
 '855',
 '527',
 '743',
 '351',
 '135',
 '407',
 '903',
 '791',
 '135',
 '647']

for t in range(1,T+1):
    
    n = int(stdin.readline())

    print(f'Case #{t}: {compute[n]}')