1. parametric search란 무엇인가1 - 합에 대한 탐색
1부터 n까지의 자연수의 합이 100이상인 경우 중 가능한 n의 최솟값을 구하는 프로그램을 작성해보세요. 단, 답은 1에서 30사이라고 가정합니다.
무작정 문제를 푼다면, 1,2,3,...,30 전까지 계속 더해보면서 최초로 합이 100을 넘는 경우, 그 숫자를 return하게 된다.
하지만 다음과 같이 시도해본다면?
1차시도: n = 15
15까지의 합은 120이므로 15는 답의 후보이며, n의 최솟값을 찾기 위해 이러한 합보다 더 작은 합은 1~14중 하나에서 찾을 수 있다.
2차시도: n = 7
7까지의 합은 28이므로, n은 확실히 7보다 커야하며, 8~14를 조사해본다.
3차시도: n = 11
11까지의 합은 66이므로, n은 확실히 11보다 커야하며, 12~14를 조사해본다.
4차시도: n = 13
13까지의 합은 91이므로, n은 13보다 커야하며, 14~14를 조사해본다.
5차시도: n = 14
14까지의 합은 105이므로, 14도 합이 100을 넘게하는 n의 한 후보이다.
더 이상 탐색할 범위가 없으므로, 가능한 후보 14,15중 최솟값인 14가 답이 된다.
앞에서는 최악의 경우 30번 시도해야하지만, 이 방법으로 5번만에 정답을 찾았다.
어떻게 이것이 가능할까
이 경우 n이 커질수록 1부터 n까지의 합이 커진다는 특징을 가지고 있다
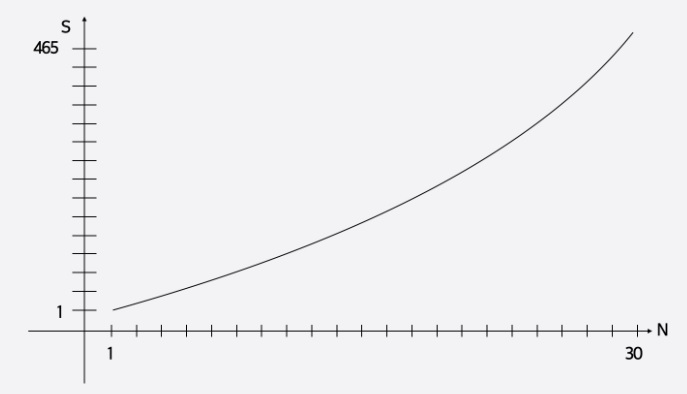
이런 경우에 1부터 n까지의 합이 100이상인 경우에서 n의 최솟값을 구할려면...
적절한 bound를 다음과 같이 설정해본다..
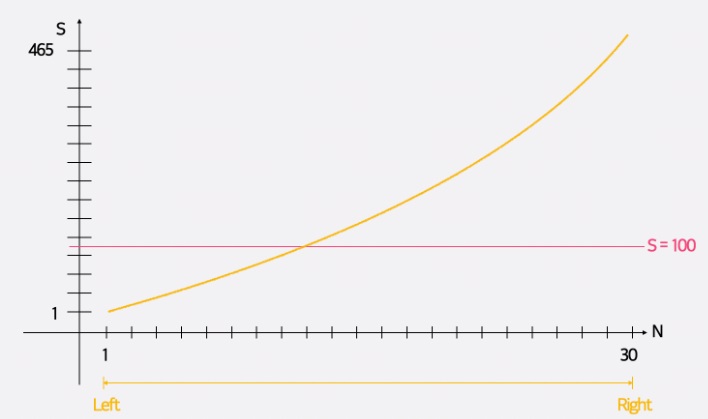
이제 구간에서 n = 15인 경우.. 합이 120으로 bound 100을 넘으므로 최솟값을 구해야하는 이 문제에서, 16 이상은 더 이상 볼 필요도 없다.
현재 가장 작은 경우가 15니까
그래서 다음 [1,14] 범위를 탐색하게 된다.
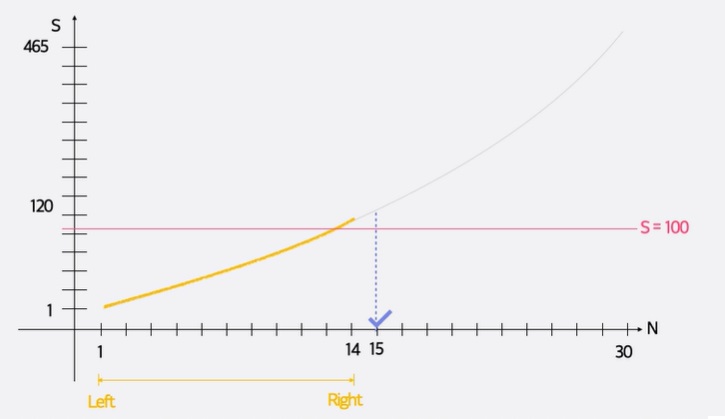
[1,14]의 중간값인 7을 확인해볼때, 7까지의 합은 28로 bound인 100을 넘지 못한다
따라서 n은 반드시 7보다 커야하며, 7보다 작은 경우는 볼 필요가 없다.
그래서 [8,14] 범위를 탐색하게 된다.

이런식으로 답이 절대 될 수 없는 범위는 버리고, 답이 되는 범위에서는 가능한 답 중 문제에서 원하는 조건에 맞는 답(여기서는 최솟값)을 계속 찾아가준다.
이렇게 답을 기준으로, 이진탐색을 진행하는 방식을 parametric search라고 부른다.
이런 설명은 처음인데

2. 연습문제
1부터 n까지의 자연수의 합이 s이하인 경우 중 가능한 n의 최댓값을 구하는 프로그램을 작성해보세요.
합 s의 최댓값이 10의 9제곱인데, s는 n의 제곱에 비례하므로 n은 아무리 커봐야 10의 5제곱보다 작다
그래서 1부터 10의 5제곱 이내에서 이분탐색을 진행
mid를 선택했으면 합은 mid * (mid+1)/2일 것이다. 여기서 타입에 주의해야하고
구한 합이 target=s 이하라면? mid는 문제 조건을 만족하는데 최댓값을 구해야하고, mid 이후로도 가능성 있으므로 start = mid + 1로 이동
하지만 target=s보다 크다면, mid 이후는 반드시 s보다 크므로, mid 이전에만 답의 가능성이 있다. 그래서 end = mid로 이동
구한 합이 s이하일때, mid는 답의 가능성이 있고, start = mid + 1로 이동했으므로, 반복문을 start = end에서 탈출하고,
end - 1을 return해야겠다.
import java.util.Scanner;
public class Main {
public static int parametricSearch(int target, int start, int end){
while(start < end){
int mid = start + (end - start)/2;
double sum = (double)mid*(mid+1)/2;
if(sum <= target){
start = mid + 1;
} else {
end = mid;
}
}
return end - 1;
}
public static void main(String[] args) {
// 여기에 코드를 작성해주세요.
Scanner sc = new Scanner(System.in);
int s = sc.nextInt();
System.out.println(parametricSearch(s,1,100001));
}
}
3. parametric search란 무엇인가2 - 몫에 대한 탐색
다음과 같이 10개의 숫자가 주어졌을 때, 칸막이를 최대 4개를 쳐서 각 칸막이를 경계로 나뉜 숫자들의 합들 중 최댓값이 최소가 되도록 하는 프로그램을 작성해보세요.
주어진 10개의 숫자 : 2 3 5 5 3 1 6 5 7 2
만약 다음과 같이 나누면
2 3 | 5 | 5 3 | 1 6 | 5 7 2
각 구간내 숫자의 합이 합이 5, 5, 8, 7, 14가 되므로 이 중 최댓값은 14가 되지만,
다음과 같이 나누면
2 3 | 5 5 | 3 1 6 | 5 | 7 2
각 구간내 숫자의 합이 5, 10, 10, 5, 9가 되므로 최댓값이 10이 됩니다. 따라서 10이 답이 됩니다.
이 문제는 어떻게 접근할 수 있을까
칸막이를 무조건 앞에 쓰자니, 뒤에 숫자들의 합이 커질 것이고,
칸막이를 무조건 뒤에 쓰자니, 어디에서 끊어야 합 중 최댓값을 최소로 만들 수 있을지 모르겠다.
하지만 이렇게 생각해본다면?
"어떤 답을 가정해봤을때, 최소가 된다 / 안된다는 판단을 해볼 수 있다"
현재 10개의 숫자 2,3,5,5,3,1,6,5,7,2의 합이 40이므로, 답은 1에서 40 사이이다.
1) 합의 최댓값이 20인 경우 설치할 수 있는지 판단해본다.
합이 20인 경우라고 명확히 설정했으니 어떤 칸막이를 어디에 설치해야할지 분명해진다
합이 20이 넘기 전까지 최대한 설치를 미루고 경계에 다다르는 순간 설치해야한다.
2 3 5 5 3 1 | 6 5 7 2
이러면 최댓값을 20으로 하는 것은 분명히 가능하다는 것이므로 20은 답의 후보가 되며,
가능한 최댓값을 최소화해야하므로, 앞으로 [1,19]에서 가능한지 탐색해본다.
2) 합의 최댓값이 10인 경우 설치할 수 있는지 판단
합의 최댓값의 상한이 10이라고 한다면...
2 3 5 | 5 3 1 | 6 | 5 | 7 2
칸막이를 4개까지 설치할 수 있는데, 4개로 해결했으니 어쨌든 최댓값이 10인 경우도 가능하다.
따라서 10은 답의 후보가 되며 가능한 최소화해야하므로, [1,9]를 탐색해본다.
3. 최댓값이 5인 경우가 가능한가?
이 경우 어떻게 해도 불가능하다.
2 3 | 5 | 5 | 3 1 | >>>> 6,5,7,2 여기서 설치 불가
따라서 최댓값은 5보다 커야하며, 그 다음으로 [6,9]를 탐색해본다.
4. 최댓값이 7인 경우가 가능한가?
2 3 | 5 | 5 | 3 1 | 6 | 5 | 7 | 2
칸막이를 4개까지 사용할 수 있으나, 여기서는 7개로 해결했으므로 최댓값이 7인 경우도 불가능하다.
따라서 최댓값의 상한은 7보다 커야하며 [8,9]를 탐색해본다.
5. 최댓값이 8인 경우가 가능한가?
2 3 | 5 | 5 3 | 1 6 | 5 | 7 | 2
칸막이를 4개까지 사용할 수 있지만, 여기서는 6개로 해결했으므로 최댓값을 8이하로 하는 것은 불가능하다.
따라서 최댓값을 더 키워야 사용하는 칸막이 수를 줄일 수 있을 것이고, [9,9]를 탐색해봐야한다.
6. 최댓값이 9인 경우가 가능한가?
2 3 | 5 | 5 3 1 | 6 | 5 | 7 2
역시 칸막이를 4개까지 사용할 수 있는데 5개로 해결했으므로 최댓값을 9 이하로 하는 것은 불가능하다.
앞으로 추가적으로 탐색할 구간이 없으므로 가능한 답의 후보 10,20중 최솟값인 10이 정답이다.
-----------------------------------------------------------------------------------------------------------------------------------
이와 같이..
1. 문제에서 어떤 답을 가정했을 때, 풀려고 하는 문제가 비교적 단순해지면서 가능/불가능을 판단할 수 있는 결정 문제로 변환되고
2. 답이 가능/불가능 할때 값이 더 커져야 할지, 작아져야 할지 분명해지는 경우
이분탐색으로 가능한 답의 범위를 O(logN)시간에 줄여가면서 각각의 답이 가능한지에 대한 결정 문제의 답을 Yes/No로 판단하는 방식을 parametric search라고 부른다.
parametric search로 특정 값이 답으로서 가능한지 판단하는 것도 쉬워지면서, 답에 대한 범위도 빠르게 줄일 수 있다.
4. 연습문제2
n개의 정수를 분배하여 같은 크기의 정수 k를 m개 만들려고 할 때, 만들 수 있는 k값의 최댓값을 구하는 프로그램을 작성해보세요. 이때, m개를 만들어야 한다는 의미는 m개 이상을 얻어내면 된다는 뜻임에 유의합니다.
단, n개의 정수를 분배할 때는 제한 없이 정수를 분배해도 괜찮지만, 각 정수에서 분배하고 남은 정수들을 합쳐서 새로운 정수로 만들 수는 없습니다.
최근에 풀었던 문제랑 비슷한 유형이다
주어진 정수 arr[i]를 k로 나눈 몫의 합이 m 이상인지 조사해서, 가능한 k의 최댓값을 구하는 문제
어떤 k를 가정하고 그 k에서 m이상인지 아닌지 조사해보는 결정문제를 해결한다.
결정문제의 정답에 따라 k의 탐색 범위를 변경해서, 최종 k를 구하면 된다.
가능한 k의 범위는?
arr의 min까지라고 자꾸 실수하지만... arr의 max까지이다.
예를 들어 500을 k = 800으로 분배할려고 한다면? 그냥 0이된다고 생각하면 될 것 같다..(문제 표현이 애매하긴 하지만..)
이런 문제 풀어봐서 알겠지만
불가능한 k가 분명히 존재하는데... 그런 경우는 k = 0으로 처리하는 것 같다(이 역시 애매한 부분이긴 하지만)
k = 0이라면 m개까지 만들면 되니까... 어떻게 보면 맞는말이기도 해서
import java.util.Scanner;
public class Main {
public static int parametricSearch(int[] arr, int m,int start, int end){
while (start < end) {
int mid = start + (end - start)/2;
int total = 0;
for(int i: arr){
total += i/mid;
}
if(total >= m){
start = mid + 1;
} else {
end = mid;
}
}
return end - 1;
}
public static void main(String[] args) {
// 여기에 코드를 작성해주세요.
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int[] arr = new int[n];
int max = 0;
for(int i = 0; i < n; i++){
arr[i] = sc.nextInt();
if (max < arr[i]){
max = arr[i];
}
}
System.out.println(parametricSearch(arr,m,1,max+1));
}
}
아무튼 arr의 정수들을 start ~ end의 mid로 나눠서 합을 구해 total이라고 한다면..
total이 m 이상이라면, mid도 정답 후보인데 가능한 k의 최댓값을 구해야하므로 mid 이후도 가능성이 있으니까, start = mid + 1로 옮긴다.
반면 total이 m보다 작다면... mid가 너무 커서 total이 작은 것이니까 mid 이전을 탐색할 필요가 있다. end = mid로 옮긴다.
start = mid가 되면 반복문을 탈출하며.. mid가 정답 후보일때 start = mid + 1로 옮겼으니 end -1을 return
---------------------------------------------------------------------------------------------------------------
매개변수의 가능한 범위를 먼저 구하고
범위 내에서 중간값을 정답이라고 가정한 다음...
그것이 실제 정답인지 아닌지 판단하는 결정문제를 해결하고
이에 따라 탐색 범위를 옮겨가서
최종 정답을 구한다
'알고리즘 > 이분 탐색' 카테고리의 다른 글
| 특정한 조건을 만족하는 정수를 찾는 방법 - 이분 탐색 제대로 활용하기 (0) | 2024.02.21 |
|---|---|
| [Java]자바 매개변수 탐색 - 배열에서 특정 수를 지우고 k번째 수를 찾는 방법 (0) | 2023.04.07 |
| 이분 탐색 응용문제로 올바른 사고 연습하기2 (0) | 2023.04.04 |
| 특별한 이분탐색 -실수 구간에서도 이분탐색이 가능할까- (0) | 2023.04.02 |
| [Java]자바로 이진탐색 연습2 -올바르게 사고하기- (0) | 2023.04.02 |

