1. 문제1
https://atcoder.jp/contests/abc341/tasks/abc341_d
D - Only one of two
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
2. 풀이
n,m,k가 주어지는데 n이나 m중 어느 하나만으로 나누어 떨어지는 정수들을 오름차순 정렬할때,
k번째로 작은 양의 정수를 찾는 문제
예를 들어 n = 2, m = 3, k = 5이면 2,3,4,8,9,10,...은 각각 2나 3중 어느 하나만으로 나누어 떨어지는 정수들이다.
4는 2로 나누어 떨어지지만 3으로 나누어 떨어지지 않는다.
여기서 5번째 정수는 9이다.
n,m이 $10^{8}$까지이고 k가 $10^{10}$까지다 보니 단순한 방법으로는 찾기 어려울 것 같다
이분탐색이 전혀 안보이는 이 문제가 이분탐색을 활용할 수 있다는게 놀랍다.
이런 형태의 문제는 다음과 같은 문제로 치환할 수 있다.
"어떤 정수 X에 대하여 조건을 만족하는 X이하의 양의 정수 개수가 K개라면 X는 조건을 만족하는 K번째 양의 정수이다."
조건을 만족하는 X이하의 양의 정수는?
1부터 X까지에서 N이나 M중 어느 하나만으로 나누어 떨어지는 정수들을 말한다.
X가 커질수록 이 개수가 점점 증가한다는 것은 명백하므로 start = 1, end = (매우 큰 값)으로 설정하고 이 사이에서
이분탐색으로 mid = X를 정하고 조건을 만족하는 개수가 K개 이상인지, 미만인지 검사하면 될것이다.
여기서 "1부터 X까지 N이나 M중 어느 하나만으로 나누어 떨어지는 정수의 개수"는 어떻게 구하는가?
https://deepdata.tistory.com/807
약수의 합 아주 빠르게 찾기 - 더블 카운팅(배수를 이용해 약수를 찾기), smallest prime factor
1. 문제 17427번: 약수의 합 2 (acmicpc.net) 17427번: 약수의 합 2 두 자연수 A와 B가 있을 때, A = BC를 만족하는 자연수 C를 A의 약수라고 한다. 예를 들어, 2의 약수는 1, 2가 있고, 24의 약수는 1, 2, 3, 4, 6, 8,
deepdata.tistory.com
X이하의 수중 N으로 나누어 떨어지는 수의 개수는 X이하의 N의 배수의 개수로 X//N개이다.
X이하의 수중 M으로 나누어 떨어지는 수의 개수는 X이하의 M의 배수의 개수로 X//M개이다.
X이하의 수중 N과 M 모두에게 나누어 떨어지는 수가 존재한다.
N과 M의 최소공배수 LCM(N,M)으로 나누어 떨어지는 수가 그것으로, X//(LCM(N,M))개가 된다.
포함과 배제의 원리에 의해서 X이하의 수중 N이나 M 어느 하나만으로 나누어 떨어지는 수의 개수는...
X//N + X//M - 2 * X//(LCM(N,M))
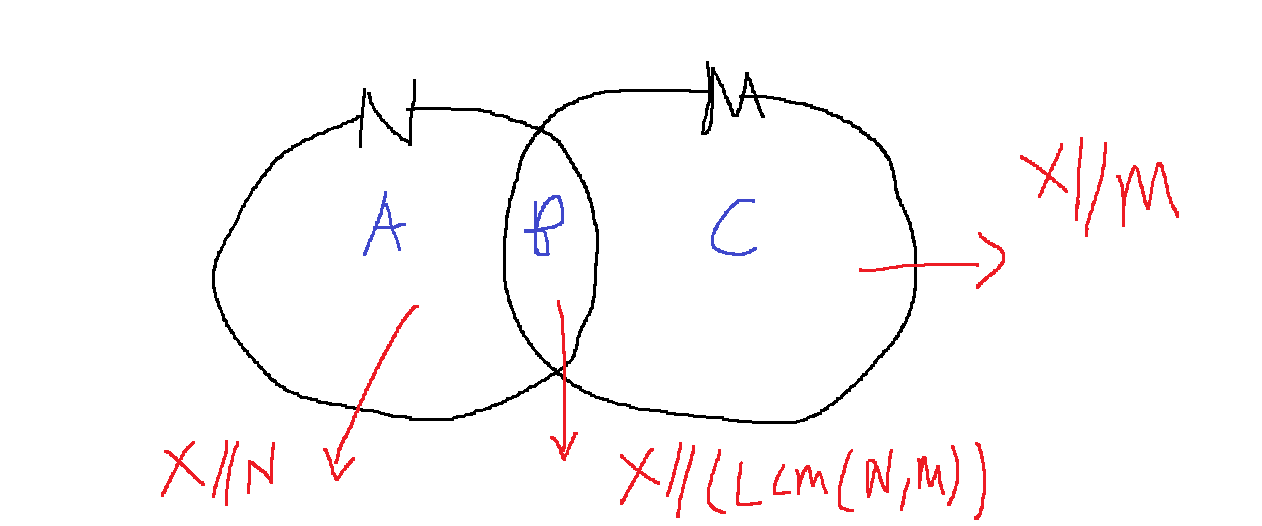
A+B = X//N이고 B+C = X//M이고 B = X//(LCM(N,M))
원하는건 A+C = X//N + X//M - 2*X//(LCM(N,M))
-------------------------------------------------------------------------------------------------------------------
다음으로 start = 1이지만 end를 어디까지 설정하고 이분탐색을 해야할까
$2*10^{18}$이내에 답이 있다는 것을 증명할 수 있다는데 무슨말인지 모르겠다
대충 k 범위가 $10^{10}$이니 적당히 $10^{20}$정도로 설정하면 충분하지 않을까?
그래서 1부터 10의 20제곱까지에서 이분탐색
X = mid로 설정하고 X이하에서 조건을 만족하는 정수의 개수를 구한다.
이게 k이상이라면 end를 mid로 좁히고 k미만이라면 start를 mid+1로 좁히면 된다.
def gcd(a,b):
while b != 0:
a,b = b,a%b
return a
def lcm(a,b):
return a*b//gcd(a,b)
n,m,k = map(int,input().split())
x = lcm(n,m)
start,end = 1,10**20+1
while start < end:
mid = start + (end - start)//2
y = mid//n + mid//m - (mid//x)*2
if y >= k:
end = mid
else:
start = mid + 1
print(end)
3. 문제2
1790번: 수 이어 쓰기 2 (acmicpc.net)
1790번: 수 이어 쓰기 2
첫째 줄에 N(1 ≤ N ≤ 100,000,000)과, k(1 ≤ k ≤ 1,000,000,000)가 주어진다. N과 k 사이에는 공백이 하나 이상 있다.
www.acmicpc.net
4. 풀이
1부터 n까지 붙여서 이어서 쓰면 하나의 긴 문자열이 될텐데 여기서 k번째 정수가 무엇인지 찾는 문제
1부터 10까지 쓰면 12345678910인데 여기서 11번째 정수는 0이다.
메모리 제한이 64mb이고 n이 최대 $10^{8}$이다 보니 배열로 저장하기에는 무리가 있고
사실 $10^{8}$정도에 2초 시간제한이면 1부터 n까지 완전탐색으로도 해볼만하긴 하다
1부터 n까지 순회해서 각각을 str()로 바꾸고 64mb 제한이다보니 매번 길이만 저장해두고
저장된 길이 + 현재 숫자의 길이가 k보다 작다면 현재 숫자에는 답이 없으니 넘어가고
저장된 길이 + 현재 숫자의 길이가 k이상이면 현재 숫자에 답이 있게된다.
이러한 숫자를 찾으면 하나씩 순회하면서 길이가 맞다면 그 정수를 출력하면 될것
n,k = map(int,input().split())
c = 0
find = False
for i in range(1,n+1):
s = str(i)
if c+len(s) < k:
c += len(s)
else:
for j in s:
if c+1 == k:
find = True
break
c += 1
if find:
break
if find:
print(j)
else:
print(-1)
그런데 pypy로 2.4초라 조금 아쉽다
첫번째 문제와 비슷하게 접근하면 될것 같다
1부터 n까지 이어쓰는데 어떤 정수 X에 정답이 있다고 생각해보자.
예를 들어 1부터 10까지 이어쓰는데 11번째 정수는 정수 X = 10에 0으로 존재했다.
그러한 정수 X를 찾는다면 X를 문자열로 바꾸고 X내에서 순회해서 길이가 맞으면 그러한 정수를 출력하면 될 것이다.
그래서 start = 1, end = n+1로 해서 이분탐색으로 X를 찾으면 좋을 것 같다.
그러면 다음 문제는 "1부터 X까지 이어붙일 때 그 길이가 얼마인지?"
1부터 X까지 이어붙일때 길이를 어떻게 빨리 구할 수 있을까
1부터 X까지 한자리수, 두자리수, 세자리수,...를 이어붙일 것이다.
123456789
101112131415161718192021....99
100101102103....999
1000....
1부터 9까지 한자리수는 9개이고 이들을 이어붙이면 1 * 9 = 9
10부터 99까지 두자리수는 90개 이들을 이어붙이면 2 * 90 = 180
100부터 999까지 세자리수는 900개 이들을 이어붙이면 3 * 900 = 2700
...
m자리수는 $9 * 10^{m-1}$개
따라서 X의 자리수가 m자리라고 한다면, m-1자리까지 이어붙인 길이를 위 방법으로 구한다.
그리고 m자리의 초기 수 10000...부터 X까지 개수를 찾는다.
X - (초기수 - 1)로 구할 수 있을 것이고 여기에 m을 곱하면 길이가 될 것
def count(n):
m = len(str(n))
result = 0
for i in range(1,m):
result += i*(9*(10**(i-1)))
result += m*(n-(10**(m-1))+1)
return result
이제 1부터 n+1사이에서 이분탐색으로 X = mid를 정한다.
1부터 mid까지 이어붙일때 길이 c를 구한다.
c가 k이상이면 end를 mid로 좁히고 c가 k보다 작다면 start = mid + 1로 좁힌다
이분탐색이 끝나면 end에 정답이 있다.
end가 탐색범위 n+1이상이라면 정답이 없는 것이고
그렇지 않다면 end - 1까지 이어붙인 길이를 찾고 end를 순회해서 길이가 k로 맞으면 그 정수를 출력하면 된다.
n,k = map(int,input().split())
start,end = 1,n+1
while start < end:
mid = (start + end)//2
c = count(mid)
if c >= k:
end = mid
else:
start = mid + 1
if end >= n+1:
print(-1)
else:
c = count(end-1)
for j in str(end):
if c+1 == k:
break
c += 1
print(j)'알고리즘 > 이분 탐색' 카테고리의 다른 글
| 실수 구간에서 이분 탐색 방법 제대로 배우기 (0) | 2024.04.07 |
|---|---|
| [Java]자바 매개변수 탐색 - 배열에서 특정 수를 지우고 k번째 수를 찾는 방법 (0) | 2023.04.07 |
| [Java]예시문제로 자바 매개변수 탐색 기본기 배우기1 (0) | 2023.04.05 |
| 이분 탐색 응용문제로 올바른 사고 연습하기2 (0) | 2023.04.04 |
| 특별한 이분탐색 -실수 구간에서도 이분탐색이 가능할까- (0) | 2023.04.02 |

