1. 문제
25707번: 팔찌 만들기
N개의 구슬을 모두 사용하여 조건에 맞게 팔찌를 만들 때 사용하는 줄의 길이의 최솟값을 출력한다.
www.acmicpc.net
2. 풀이
서로 인접하는 구슬 사이 차이가 최소가 된다면 전체 줄의 길이가 최소가 될 것 같다
구슬의 크기를 담은 리스트를 오름차순 정렬하면 서로 인접하는 값들의 차이가 최소가 될 것
0번 1번 차이
1번 2번 차이
2번 3번 차이
...
n-2번 n-1번 차이들의 합에
원형으로 배열하니까 마지막 n-1번과 0번의 차이도 구해서 더해주면 될 것
from sys import stdin
n = int(stdin.readline())
ball = list(map(int,stdin.readline().split()))
ball.sort()
answer = 0
for i in range(n-1):
answer += ball[i+1]-ball[i]
print(answer+(ball[n-1]-ball[0]))
3. 애드 혹
조금만 생각해보면 아주 간단하게 풀 수 있다
구슬에 적힌 수의 최솟값을 min, 최댓값을 max라고 하자
그리고 구슬을 임의의 순서로 원형 배열한다고 해보자
그러면 min부터 max까지 임의의 순서대로 원형으로 배열이 되어 있을 것이다.
min에서부터 시작해서 원형으로 구슬을 순회한다고 생각해보자
어떻게 돌더라도 max가 적힌 구슬을 반드시 만나게 된다
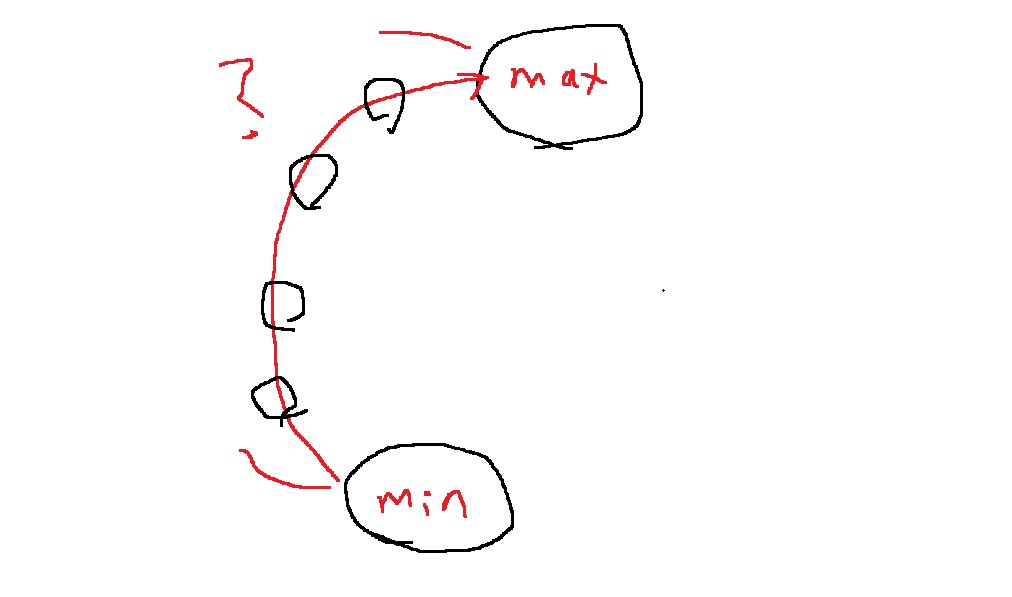
그러면 위 그림에서 min에서 max까지 가는 동안 그 실의 길이는 얼마가 될까?
min과 max 사이에 구슬이 어떻게 배치되더라도... max-min보다 작을 수는 없을 것이다
아니 근데 max-min보다 클수가 있나??
예를 들어 1,3,7,10이 있다고 해보자..
1,3,7,10으로 배치 된다면.. 2+4+3 = 9이고 10-1 = 9로 최솟값
1,7,3,10으로 배치 된다면... 6+4+7 = 17로 9보다 커지네...
아무튼 min에서 움직여서 max로 왔다면, 반대로 max에서 min으로 간다면?
마찬가지로 그 사이를 어떻게 배치하든지간에 max-min이 최소가 된다
따라서 실의 전체 길이의 최솟값은 2*(max-min)이 된다
어떻게 배치하든지 간데 2*(max-min)이 되도록 배치할 수 있다면, 그 길이가 최소가 된다는 뜻이다
그리고 그렇게 배치하는 방법은 적힌 수의 크기를 기준으로 오름차순 정렬한다음에 처음(최소)과 끝(최대)을 연결하면
그러한 경우가 최소가 되는 경우이다.
왜냐하면... 수직선 위에 수를 배열한다고 생각해보면 너무나 당연하다
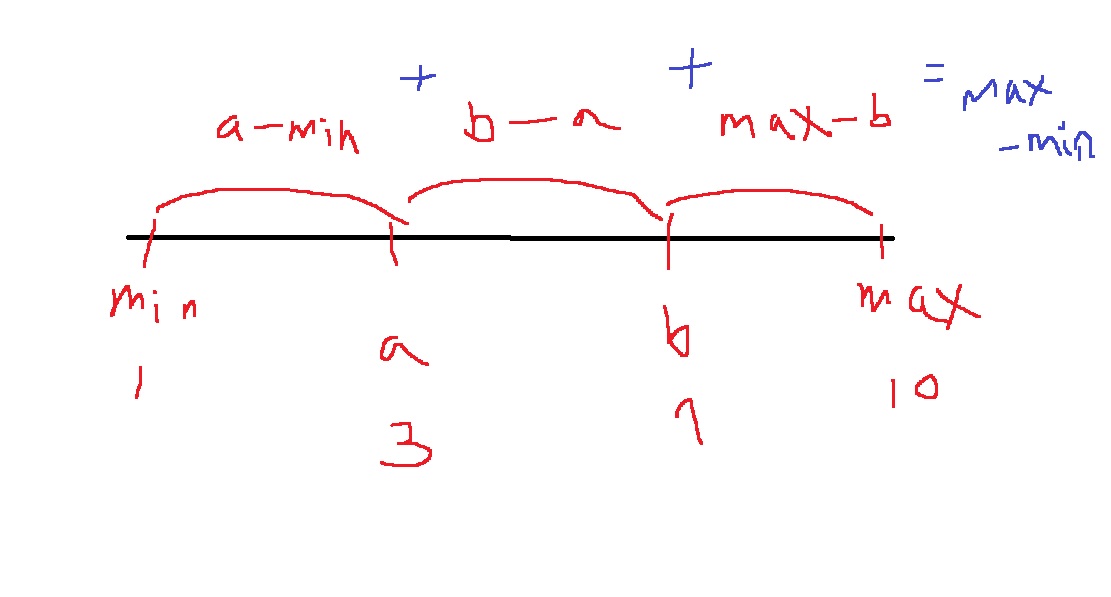
그리고 이 경우가 생각해보면 인접한 사이의 값들이 최소가 되도록 정렬했던, 위에서 했던 풀이와 동일하다
from sys import stdin
n = int(stdin.readline())
ball = list(map(int,stdin.readline().split()))
ball.sort()
print(2*(ball[-1]-ball[0]))
'알고리즘 > 애드 혹 알고리즘' 카테고리의 다른 글
| XOR 문제에 접근하기 위해 반드시 필요한 스킬1 - 기본 성질 - (0) | 2024.01.23 |
|---|---|
| ABC 334 복기 - 배열에서 원소 하나를 제거해서 두 원소 절댓값 차이의 합을 최소로 만들기(prefix sum, suffix sum) (0) | 2024.01.01 |
| 의외로 알아내기 어려운 2의 거듭제곱을 더하면 나타나는 특징 (0) | 2023.10.09 |
| 100번할 것을 1번만에 하는 나눗셈 연산 -시험 감독- (0) | 2022.11.03 |
| 매우 큰 수를 나머지 연산으로 줄일 수 있는 마법(백준-개미) (0) | 2022.08.30 |

