1. RNN의 기본 구조
일반적으로 데이터 사이에 서로 영향을 주지 않고 시간적 정보가 없는 경우가 많다.
하지만 시계열과 같은 순차적 데이터(sequential data)는 과거가 미래에 영향을 주므로 데이터 사이에 독립을 가정한 모형을 적합시키면 좋은 성능을 기대하기 어렵다.
Recurrent Neural Network(RNN)는 음성 인식과 자연어 처리와 같이 순차적 데이터에 사용되는 대표적인 알고리즘
Long Short term memory(LSTM)와 Gated Recurrent Unit(GRU)의 근간이 되는 모델
인공신경망과 CNN은 입력층에서 은닉층으로, 은닉층에서 출력층으로 움직이는 순방향 신경망(Feed forward neural network)
반면 RNN은 입력층에서 출력층(x -> y)으로 입력값을 내보내는 동시에 다음 시점의 은닉층 $h_{t}$ -> $h_{t+1}$로도 입력이 흐르는 형태

보통 오른쪽의 구조를 간단하게 왼쪽의 순환 구조로 나타낸다
매 시점 t의 정보가 다음 시점 t+1로 넘어간다
RNN은 입력 x와 출력 y, 그리고 RNN Cell이라는 은닉층 h로 구성된다.
$x_{1}, x_{2},... ,x_{t}$는 순차적 입력 데이터를 의미한다.
t시점의 RNN Cell은 t시점의 입력 데이터 $x_{t}$와 $h_{t-1}$을 입력받고,
$x_{t}$에 대한 가중치 $W_{x}$와 $h_{t-1}$에 대한 가중치 $W_{h}$ 2개를 가지며,
활성함수로 tanh함수를 사용하여 다음시점의 $h_{t}$는 다음과 같이 구한다.
$$h_{t} = tanh(W_{x}x_{t} + W_{h}h_{t-1})$$
그러면 이 $h_{t}$는 다음 시점 t+1의 은닉층으로 넘어가며, t시점의 출력값이 필요할때는 현재 시점에서 task의 목적에 맞는 적절한 활성함수 $f_{y}$에 대하여..
$$y_{t} = f_{y}(W_{y}h_{t})$$
2. RNN의 유연한 구조 변경
RNN은 다양한 입출력 형태에 따라 유연하게 네트워크 구조를 설계할 수 있고, 그만큼 다양한 문제에 적용할 수 있다.

One to Many: Image Captioning - 이미지를 설명할 수 있는 문장을 생성하는 문제
Many to One: Sentiment Classification - 텍스트에서 정보를 추출하여 감정, 태도를 파악하는 감성 분석
Delayed many to many: machine translation - 입력된 언어를 다른 언어로 변환하는 기계 번역
Many to Many: 동영상의 각 이미지 프레임별 분류
----------------------------------------------------------------------------------------------------------------------------------
하지만 RNN에서 입력과 출력 사이의 시점이 멀어질수록 그 관계가 학습되기 어려우며, 가까운 시점의 입력만 잘 기억한다는 한계가 있었다.
이를 극복하기 위해 여러 RNN의 변형 모델이 등장했다.
3. Long term dependency problem
RNN에서 입력과 출력시점이 멀어질수록 학습이 잘 안되는 현상을 Long term dependency problem이라고 한다.
예를 들어 "나는 민수와 밥을 먹고 있다. 그는 피자를 좋아한다."라는 짧은 문장에서, "그"라는 지칭이 "민수"임을 쉽게 알 수 있다.
그런데, "나는 오늘 오후에 민수를 만나기로 했다. 집을 나서기 전, 남동생과 함께 게임을 했다. ... 오후에 약속 장소인 피자집에 도착했다. 피자는 그가 가장 좋아하는 음식이다."라는 긴 문장에서
"그"라는 지칭이 "민수"라는 것을 알기 위해서는 단락의 첫 문장 정보까지 사용해야한다.
RNN의 특징은 과거의 정보를 은닉층에 저장하는 것인데, 이로 인해 치명적인 단점이 발생하게 된다.
매 시점이 지날수록 $h_{t} = tanh(W_{x}x_{t} + W_{h}h_{t-1})$의 가중치와 활성함수가 누적되어 곱해지면서, 과거의 정보가 점점 잊히는 것이다.
4. LSTM의 기본구조
LSTM은 RNN구조에 몇가지 기능을 추가해서, Long term dependency problem을 해결한 모델이다.

RNN은 활성함수 하나로 구성된 은닉층이 반복되는 구조였지만, LSTM은 위와 같이 상호작용하는 여러 모듈이 속한 구조가 반복된다.
여러 모듈로 구성된 A부분을 LSTM cell이라고 부르고, 하나를 떼서 확대해보면 다음과 같다.

$\sigma$는 sigmoid function을 나타내고, x 표시는 element-wise multiplication, + 표시는 element-wise summation을 나타낸다.
LSTM은 3개의 입력을 받는다.
$x_{t}$는 현재 시점의 입력데이터, $h_{t-1}$은 이전 시점 cell의 출력, $C_{t-1}$은 이전 cell의 정보이다.
LSTM cell의 출력은 $h_{t}$와 cell의 정보 $C_{t}$이다.
결국 LSTM cell은 현재 입력 데이터, 이전의 출력 데이터, 그리고 이전 cell 메모리를 통해 현재 시점의 출력 데이터를 예측하고, 메모리를 업데이트한다.
5. cell state
LSTM의 핵심 $C_{t}$가 흐르는 길은 cell state라고 부르며 RNN에는 존재하지 않는다.
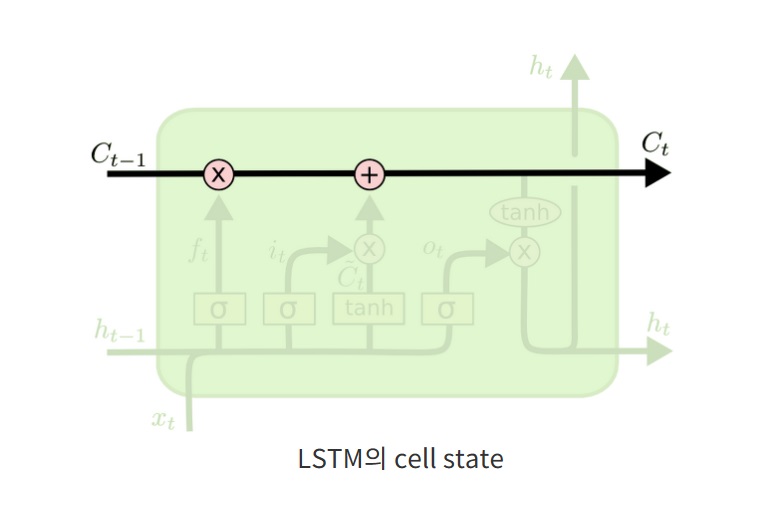
각 연산에는 과거의 정보를 얼마만큼 기억하고, 현재의 데이터를 얼마만큼 더할 것인가를 조절한다.
"얼마만큼"의 정도는 수도꼭지의 밸브 역할을 하는 Gate에 의해 정해진다.
Cell state는 Forget Gate와 Input Gate 2개와 연결된다.
6. forget gate
forget gate는 "과거 메모리를 얼마나 기억할 것인가"에 대한 의사결정을 해주는 gate
아래 수식은 $h_{t-1}$와 $x_{t}$를 입력받아, sigmoid를 적용하여 0에서 1 사이의 값으로 출력하는 forget gate를 표현하고 있다.
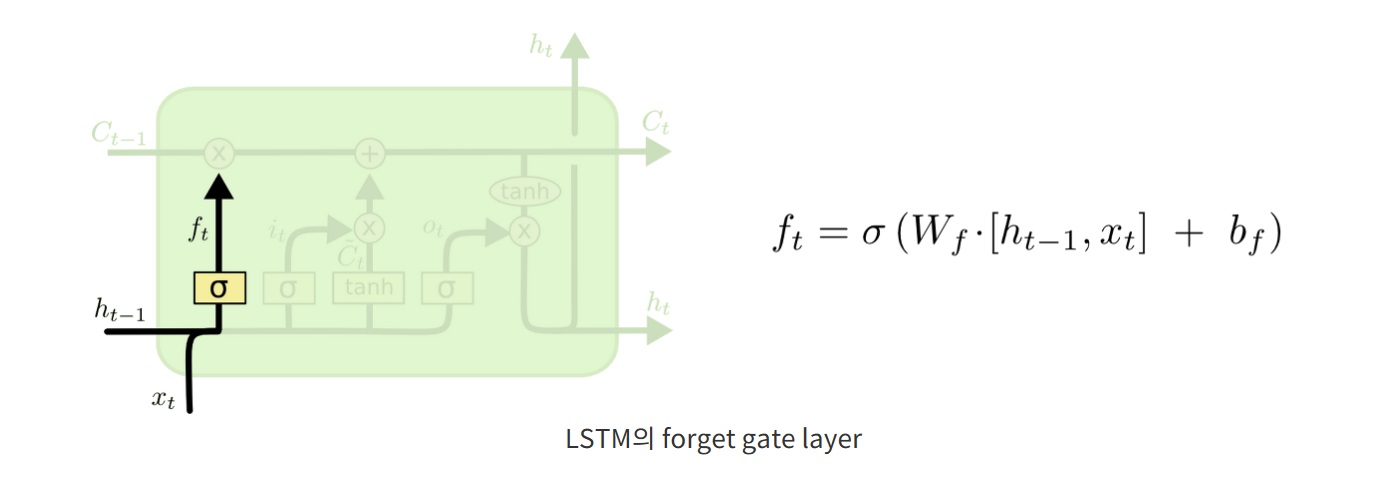
만약 $f_{t}$가 0이라면, 과거 시점의 Cell state값인 $C_{t-1}$와 곱해져, 과거 메모리를 완전히 잊어버리고,
$f_{t}$가 1이라면, $C_{t-1}$을 전부 기억하라는 뜻이 된다.
7. input gate
"현재 정보를 과거 메모리에 얼마만큼 더할 것인가"에 대한 의사결정을 하는 gate
input gate는 sigmoid와 tanh 활성 함수로 적용된 두개의 모듈로 구성

위 수식에서 $i_{t}$는 "얼마만큼"의 정보를 더해줄 것인지를 결정하고, $\tilde{C_{t}}$은 cell state에 더해질 정보를 나타낸다.

$$C_{t} = f_{t} \times C_{t-1} + i_{t} \times \tilde{C_{t}}$$
이전 시점의 cell state정보에서 일부를 걸러내고, 현재 시점으로 들어온 입력중 일부가 더해져서 업데이트 된다.
8. output gate

현재 시점의 출력 $h_{t}$는 output gate에서 구해진다.
입력인 $x_{t}$와 $h_{t-1}$에 sigmoid를 적용하여, 입력의 일부와 업데이트된 cell state $C_{t}$에 의해 구해진다.
즉 업데이트된 cell state정보 $C_{t}$중에서 현재 입력으로 들어온 $x_{t}$와 $h_{t-1}$을 바탕으로 $o_{t}$를 계산하여 어떤 부분을 출력으로 보낼지 결정하게 된다.
LSTM은 forget, input, output gate와 cell state라는 차별화된 특징으로 RNN의 Long term dependency 문제를 극복하였다.
LSTM의 뛰어난 예측력은 실제로 많은 연구와 활용에서 포착되고 있지만, LSTM cell 자체가 복잡하다보니 연산속도가 느리다는 단점이 있다.
이러한 단점을 극복하고자 LSTM을 간소화한 Gated Recurrent Units(GRU)가 개발되었다..
실제로는 둘이 연산량은 비슷하다던데
참조
GoldenPlanet | 빅데이터 공부 한 걸음: RNN(순환 신경망)이란?
Go Beyond Data! 골든플래닛
goldenplanet.co.kr
[Deep Learning (딥러닝)] RNN의 다양한 형태! : 네이버 블로그 (naver.com)
[Deep Learning (딥러닝)] RNN의 다양한 형태!
RNN(Recurrent Neural Network)의 다양한 형태에 대해서 잠시 둘러보자. 먼저 알아 볼 것은 one-to-o...
blog.naver.com
LSTM(Long Short Term Memory networks) : 네이버 블로그 (naver.com)
LSTM(Long Short Term Memory networks)
1. LSTM이 나타나게 된 배경 LSTM은 장기의존성 문제를 해결하기 위해 디자인되었다. 오랜 기간동...
blog.naver.com
LSTM의 원리와 수식 계산 · The Missing Papers (likejazz.com)
LSTM의 원리와 수식 계산 · The Missing Papers
LSTM의 원리와 수식 계산 30 May 2018 LSTM은 RNN의 핵심을 이루는 모델이다. 그러나, 구체적인 구현에 대해 잘못 이해하고 있는 경우가 많다. 원리를 정확히 이해하는 일은 매우 중요한 만큼 여기서는
docs.likejazz.com
Long Short-Term Memory (LSTM) 이해하기 :: 개발새발로그 (tistory.com)
Long Short-Term Memory (LSTM) 이해하기
이 글은 Christopher Olah가 2015년 8월에 쓴 글을 우리 말로 번역한 것이다. Recurrent neural network의 개념을 쉽게 설명했고, 그 중 획기적인 모델인 LSTM을 이론적으로 이해할 수 있도록 좋은 그림과 함께
dgkim5360.tistory.com
'딥러닝 > NLP' 카테고리의 다른 글
| NLP에서 language model의 역사 훑어보기 (0) | 2023.05.08 |
|---|---|
| text data를 다루는 NLP + computer vision과의 활용 - image captioning 기본 배우기1 (0) | 2023.02.27 |
| NLP에서 경량화를 시도하려는 연구들 알아보기 (0) | 2022.10.28 |
| BERT를 가볍게 만드려는 시도 - ALBERT 모델 공부하기 (0) | 2022.10.27 |
| GAN의 원리에 착안한 ELECTRA와 학습하지 않아도 응용을 잘하는 GPT-3 (0) | 2022.10.26 |

