1. entropy를 줄이는 방법
무질서도를 측정하는 측도로 무작위할수록 높은 값을 갖는다.
색이 맞은 완전한 큐브는 단 1가지의 경우의 수(state)를 가지지만 색이 흐트러져 뒤섞인 큐브는 무수히 많은 경우의 수(state)를 가진다.
열역학 제 2법칙은 닫힌 공간에서 엔트로피는 항상 증가하는 방향으로 흐른다는 것이다.
시간이 과거에서 미래로 흐르는 것도 미래가 과거보다 무작위하다는 것을 생각하면 자연스럽다
그러나 공간에 에너지를 투입하는 경우 global하게 닫힌 공간으로 확장하면 엔트로피는 증가하지만 에너지를 투입한 local한 부분에서는 엔트로피를 감소시킬 수 있다
멋진 말로는 부분 공간에서는 시간을 잠깐 거슬러 올라갈 수 있다는것?
색이 흐트러져 뒤섞인 큐브는 무작위로 뒤섞여 엔트로피가 높은 상태
그러나 여기에 사람이 에너지를 투입하면 완전한 큐브로 바꿀 수 있고 완전한 큐브는 unique한 상태이므로 엔트로피가 낮은 상태
머신러닝도 마찬가지로 개와 고양이가 뒤섞인 무작위한, 엔트로피가 높은 dataset에서
머신러닝 모델에 training 비용같은 에너지를 투입하여 완전한 분류를 수행하면 엔트로피를 감소시킨다
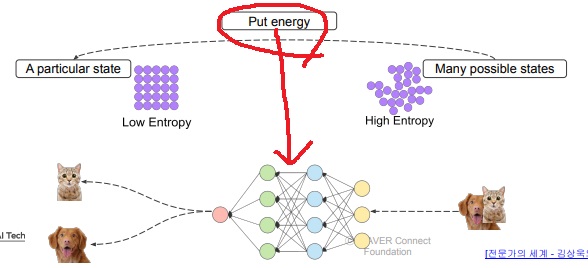
모델 training 비용, 에너지를 투입하여 entropy가 높은 상태에서 낮은 상태로 이동시켰다
2. random variable의 entropy
random variable의 가능한 결과들이 내재하는 놀라움의 정도, 불확실한 정도, 정보량의 정도를 기댓값으로 나타낸 것

base는 사용하는 상황?에 따라 다르다 보통은 2, 10, e를 사용
random variable이 uniform 분포를 따르면, 모든 사건이 동일한 확률로 나타나면, entropy가 가장 높은 상태이다.
직관적으로 어떤 사건이 나와도 당연하다는 느낌, 놀랍다는 느낌이 없는 완전하게 무작위한 상태라서 그렇다
바꿔말하면 어떤 것이 더 낫고 어떤 것이 더 나쁜지 정할 수 없는 상태
더 쉽게 말하면 아무런 정보가 없는 상태이다.
uniform 분포에서 어떤 지식이나 어떤 정보가 포함되어 어떤 사건이 나올 확률이 달라진다면 low entropy가 되는 것이다.

3. 동전 던지기
동전을 던져 앞면이 나올 확률은 1/2이고 뒷면이 나올 확률은 1/2이면 entropy는?
동전 던지기 사건은 앞면 아니면 뒷면 2가지이므로 $log_{2} 2$ = 1bit의 정보량으로 나타낼 수 있다.
따라서 entropy는 사건의 정보량의 가중평균으로 구해진다.
앞면의 가능성은 1/2이니 1bit의 절반으로 뒷면도 가능성이 1/2이니 1bit의 절반으로 나타낼 수 있고 이것의 합이 entropy로 1이다.
확률이 동일한 상태이므로 entropy가 가장 높은 1이 나올 것임은 계산안해봐도 예상이 가능

entropy가 1인 것은 아무런 정보가 없는 상태나 마찬가지이다.
여기에 동전이 휘어있어서 앞면이 나올 확률이 2/3이고 뒷면이 나올 확률이 1/3이면?
$\frac{2}{3} \times log_{2} \frac{3}{2}$ + $\frac{1}{3} \times log_{2} 3$=0.92로 동전이 휘어있다는 정보가 추가되어 entropy가 떨어진 사실을 확인할 수 있다.
4. 모델의 time이란
모델이 소모하는 단순한 연산 시간으로의 개념
모델이 high entropy 상태인 input에서 low entropy 상태인 output으로 시간을 역전시키는데 들어가는 정보와 노력으로의 개념???
근데 위에거 단순한 연산 개념이 input에서 output으로 바꾼다는 아래 내용을 포괄하는거 아닌가
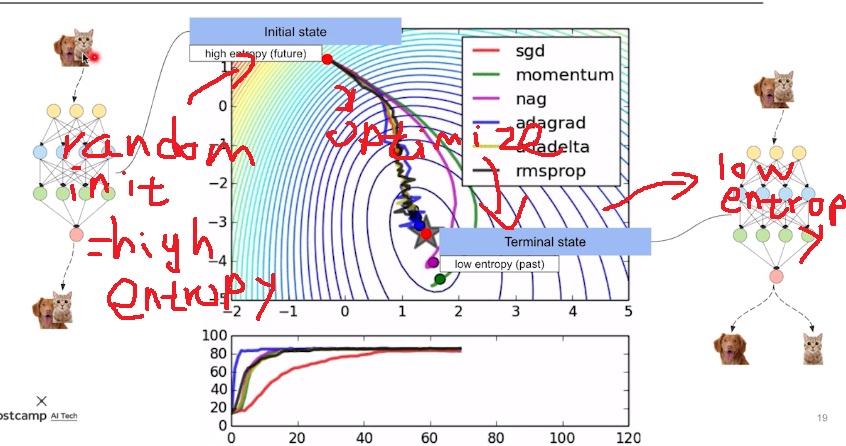
random하게 initialization된 상태는 무작위한 상태이므로 high entropy
아무런 정보가 없어서 개+고양이 섞어서 줘도 개+고양이를 분류하지 못함
데이터나 정보를 주어 optimization을 하면 low entropy상태가 되어 개+고양이를 개와 고양이로 분류해냄
5. 게임에서 entropy?
게임의 첫 시작은 unique한 상태(애매하긴 한데)이므로 low entropy이고
게임을 시작하면 자연스럽게 여러가지 예측할 수 없는 상황이 섞여 무작위해져서 high entropy
여기에 플레이어의 비용, 노력, 전략들이 들어가면서 게임 1판을 끝내면 terminal state가 되어 entropy가 줄어들어서 low entropy가 된다
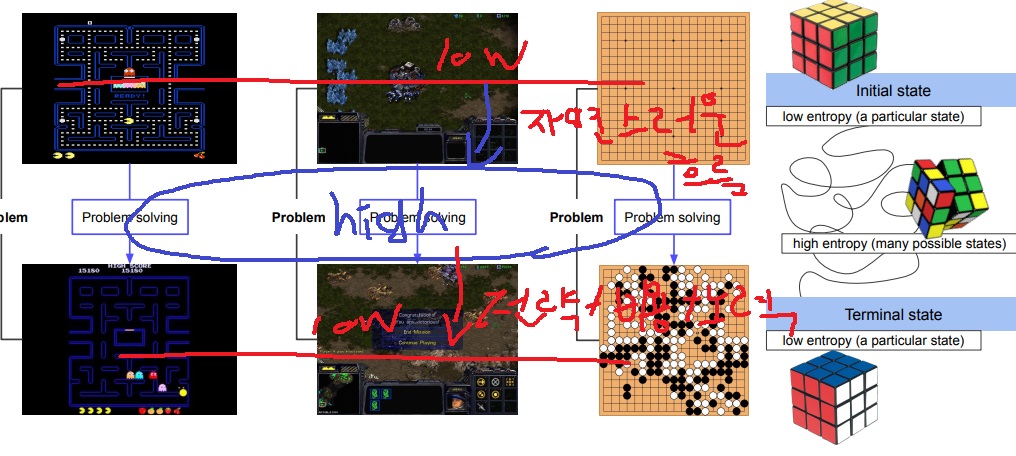
게임을 시작하면 entropy가 증가하여 무작위한 상황이 생기지만
여기에 플레이어의 노력, 전략이 들어가 low entropy가 되어 게임이 끝난 상태가 된다.
'딥러닝 > light weight modeling' 카테고리의 다른 글
| 머신러닝 관점에서 information transmission (0) | 2022.11.03 |
|---|---|
| 딥러닝에서 parameter search하는 gradient descent와 기하학적 의미 (0) | 2022.11.02 |
| 공간(space)과 시간복잡도(time) 사이 관계 (0) | 2022.10.31 |
| MNasNet과 PROXYLESSNAS와 ONCE-FOR-ALL network 알아보기 (0) | 2022.04.05 |
| NAS(Neural Architecture Search) 기법에 대해 알아보기 (0) | 2022.03.20 |

