1. 문제
자연수로 이루어진 어떤 수열이 주어질때, 이 수열의 모든 부분수열의 합을 생각해보자
이때 불가능한 합의 최솟값을 구해본다면?
예를 들어 s = [5,1,2]이면, 1,2,3,5,6,7,8은 만들 수 있는데 4를 만들 수가 없다
2. 알고리즘
2-1) 수열을 오름차순으로 정렬한다
2-2) sum = 0로 초기화한다
2-3) 수열을 하나씩 순회해서 그것을 x라고 하자. sum+1을 만들 수 있는지 확인해본다.
2-4) sum+1 >= x이면 sum+1까지 만들 수 있다. 그러면, sum + x를 sum으로 갱신한다.
2-5) sum+1 < x이면, sum+1은 만들 수 없는 합이고 반복문을 종료하면 sum+1이 최솟값이다.
이것만 보면 아무리 생각해도 와닿지는 않는다
어떻게 보면 경이롭기까지하다. 진짜 이게 가능한건가?
여러가지 풀이를 보면서 이해해보도록 노력하자
3. 예시를 통해 이해해보기
수열 1,2,3,5,13이 주어졌다고 해보자.
3-1) sum = 0은 아무것도 안쓰고도 만들 수 있다
그러면 수 1을 이용해서 sum+1 = 1을 만들 수 있는지 확인해본다
sum+1 >= 1이므로, 1을 만들 수 있다.
1 = 1이므로 1을 만들 수 있다.
그래서 sum = sum + 1 = 1로 갱신한다.
이것은 1까지는 만들 수 있다는 뜻이다.
3-2) 다음 수 2를 이용해서 sum+1 = 1+1=2를 만들 수 있는지 확인해본다.
sum+1 >= 2이므로, 2를 만들 수 있다.
2 = 2이므로 2를 만들 수 있다
그래서 sum = sum + 2 = 3으로 갱신한다.
이것은 3까지는 만들 수 있다는 뜻이다.
1 = 1
2 = 2
3 = 1+2
3-3) 다음 수 3을 이용해서 sum+1 = 3+1=4을 만들 수 있는지 확인해본다.
sum+1 >= 3이므로, 3을 만들 수 있다.
1 = 1
2 = 2
3 = 1+2
4 = 1+3
5 = 2+3
6 = 1+2+3
으로 6까지 만들 수 있다. 그래서 sum = sum+3 = 6으로 갱신한다.
3-4) 다음 5를 이용해서 sum+1 = 6+1=7을 만들 수 있는지 확인해본다.
sum+1 >= 5이므로 5를 만들 수 있다
1 = 1
2 = 2
3 = 3
4 = 1+3
5 = 2+3
6 = 1+2+3
7 = 2+5
8 = 3+5
9 = 1+3+5
10 = 2+3+5
11 = 1+2+3+5
으로 11까지 만들 수 있다. 그래서 sum = 6+5 = 11로 갱신한다
3-5) 다음 sum+1=12를 13을 이용해서 만들 수 있는지 확인해본다.
하지만, sum+1 < 13이므로 12는 절대로 만들 수 없다.
그래서 만들 수 없는 합의 최솟값은 12가 된다
알듯 말듯하면서도 왜 그런지 와닿지 않아 놀랍다
4. 그림으로 이해해보기
아주 완벽하게 풀어낸 분이 계셔서 아이디어를 카피?했다
백준 2437 풀이 및 해설 (aerocode.net)
백준 2437 풀이 및 해설
개요 매우 복잡해보이는 문제가 그림으로 풀면 매우 단순하게 풀리는 경우 는 그리 드문일이 아닙니다. 이 문제는 수학적 귀납법으로도 풀 수 있지만, 수직선을 사용하면 훨씬 직관적이고 쉽게
aerocode.net
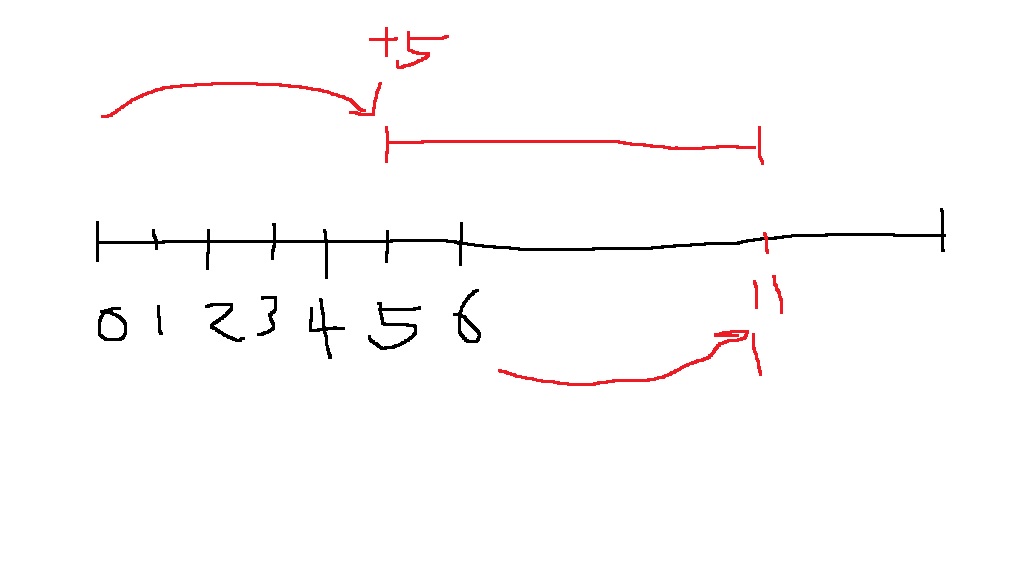
내가 만약에 0~6까지 만들 수 있다고 생각해보자.
여기에 수 5가 추가로 주어진다면, 나는 5~11까지를 추가로 만들어 볼 수 있다는 뜻이다.
간단하게 생각해보면.
0 (아무것도 안씀)
1 = 1
2 = 2
3 = 1+2
4 = 1+3
5 = 2+3
6 = 1+2+3
여기에 각각 5만 더해보면 되니까
5 = 5
6 = 1+5
7 = 2+5
8 = 1+2+5
9 = 1+3+5
10 = 2+3+5
11 = 1+2+3+5
----------------------------------------------------------------------------
근데 수 6이 추가로 주어진다면 어떨까
6부터 12까지 추가로 만들 수 있다
역시 그냥 6을 더해보면 된다
6 = 6
7 = 1+6
8 = 2+6
9 = 1+2+6
10 = 1+3+6
11 = 2+3+6
12 = 1+2+3+6

--------------------------------------------------------------
만약 7이 추가로 주어진다면 어떨까
7부터 13까지 추가로 만들 수 있다
7 = 7
8 = 1+7
9 = 2+7
10 = 1+2+7
11 = 1+3+7
12 = 2+3+7
13 = 1+2+3+7

--------------------------------------------------------------
그렇다면 만약 8이 추가로 주어진다면 어떨까??
8부터 14까지 추가로 만들 수 있다
0~6까지 만든 경우에 8을 더하기만 하면 되니까
하지만 7을 만들 수 있을까? 절대로 불가능하다
1,2,3,8을 한번씩만 가지고 7을 만들 수 있는가? 아무리 생각해도 불가능하다.
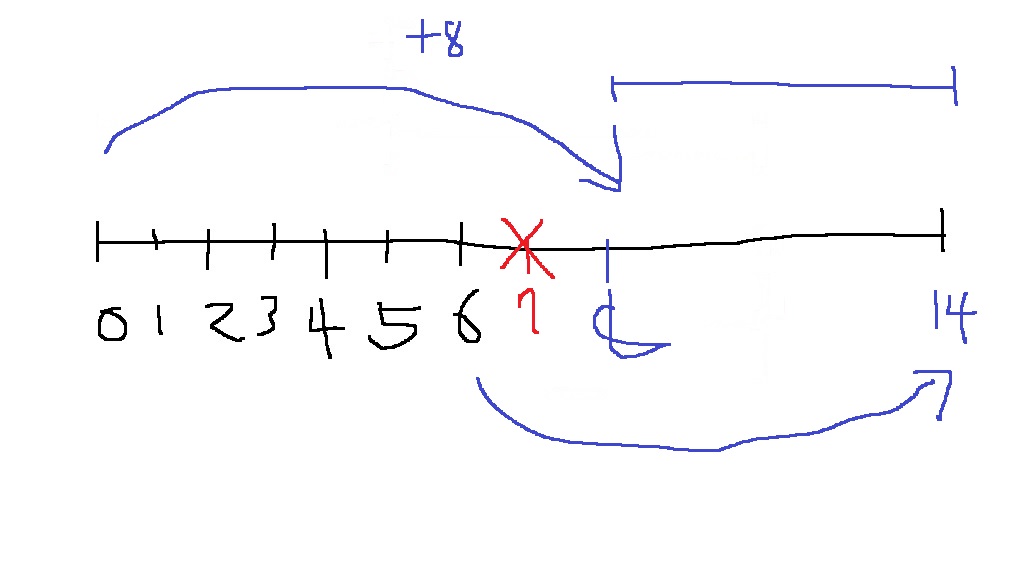
이 문제의 핵심은 만들 수 있는 합의 구간으로부터, 어떤 수가 추가로 주어질때, 내가 추가로 만들 수 있는 구간이 서로 이어지느냐? 끊어지느냐이다
위 그림을 잘 생각해보면, 내가 만들 수 있는 합의 구간이 0~sum으로 주어진다면
최댓값 sum은 가지고 있는 모든 수의 합이다.
수열의 다음 수 $a_{n+1}$이 주어질때, 추가로 만들 수 있는 구간은 $a_{n+1}$에서 $sum+a_{n+1}$이다.
만약 이 구간이 끊어지지 않고 계속 이어질려면..
\[ sum+1 \geq a_{n+1}\]
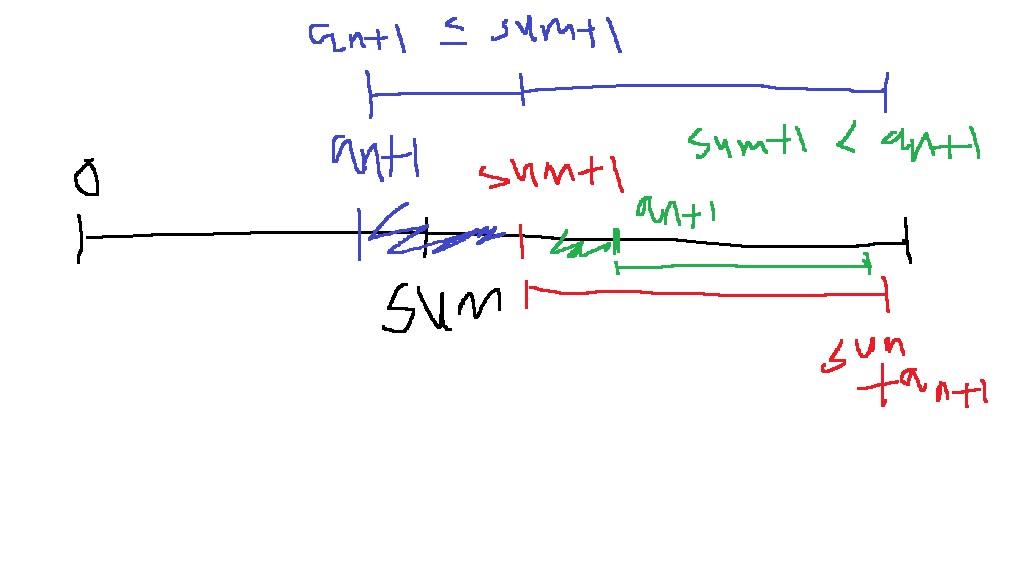
만약에 sum+1이 $a_{n+1}$보다 크거나 같다면, 추가로 $a_{n+1}$부터 $sum + a_{n+1}$까지 만들 수 있으므로
다음 sum을 $sum + a_{n+1}$로 갱신한다면, 우리는 0부터 $sum + a_{n+1}$까지 만들 수 있게 되는 것이다.
하지만 sum+1이 $a_{n+1}$보다 작다면, sum+1부터 $a_{n+1}-1$까지는 만들 수 없다는 뜻이다.
이게 바로 이 문제의 핵심 해법이었다
그림으로 같이 보니까 명확하네
4. 연습문제1
14225번: 부분수열의 합
수열 S가 주어졌을 때, 수열 S의 부분 수열의 합으로 나올 수 없는 가장 작은 자연수를 구하는 프로그램을 작성하시오. 예를 들어, S = [5, 1, 2]인 경우에 1, 2, 3(=1+2), 5, 6(=1+5), 7(=2+5), 8(=1+2+5)을 만들
www.acmicpc.net
자연수의 수열이 주어질때, 부분 수열의 합으로 나올 수 없는 가장 작은 자연수를 구하는 문제
5. 풀이1
당연히 완전탐색으로 풀었었다..
원소의 최댓값이 10만이고 길이가 20이 최대니까 cnt배열을 최대 200만 길이로 만들어주고
모든 부분집합을 구하고 합을 구해본 다음에 cnt배열에 넣어준다
다시 cnt배열을 인덱스로 순회해서 최초로 cnt배열의 값이 0이라면, 그러한 인덱스값은 합으로 존재하지 않았다는 뜻이다
from sys import stdin
#길이가 20이 최대이고, 원소는 10만이 최대니까
cnt = [0]*((20*100000)+1)
n = int(stdin.readline())
s = list(map(int,stdin.readline().split()))
#모든 부분집합을 탐색
#합을 구해서 cnt배열에 넣어본다
for i in range(1<<n):
partial = 0
for j in range(n):
if i & (1<<j):
partial += s[j]
cnt[partial] += 1
#cnt배열을 다시 탐색해서, 처음으로 0이 나오는 부분에서 멈춘다
for i in range(1,(20*100000)+1):
if cnt[i] == 0:
break
#0이 나온 부분은 그 합이 존재하지 않는다는 뜻이므로
print(i)
6. 풀이2
위에서 배운 알고리즘으로 해결해보자
4000ms 걸리던 풀이가 70ms로 압도적으로 줄어든다
수열을 먼저 오름차순으로 정렬하고
최초 sum_value = 0으로 초기화하자
내가 0~0까지 만들 수 있다는 뜻이다.
s에서 작은 수 num부터 꺼내서 만들 수 있는 수의 최댓값인 sum_value +1보다 num이 더 크다면...
sum_value+1 ~ num-1까지는 만들 수 없다는 뜻이다
그러므로 반복문을 탈출하고 sum_value+1이 만들 수 없는 수의 최솟값이다
반대로 sum_value+1이 num이상이라면, 0~sum_value+num까지를 나는 이제 만들 수 있게 되었다
from sys import stdin
n = int(stdin.readline())
#수열을 오름차순으로 정렬
s = sorted(map(int,stdin.readline().split()))
#처음에 0~0까지 만들 수 있다
sum_value = 0
#작은 수부터 꺼내서,
for num in s:
#나온 수가 만들 수 있는 수의 최댓값+1보다 크다면,
#만들 수 있는 수의 최댓값+1부터 num-1까지는 만들 수 없는 수이다.
if sum_value+1 < num:
break
#만들 수 있는 수의 최댓값+1이 num이상이라면,
#그러면 나는 0~sum_value+num까지 이제 만들 수 있게 되었다.
sum_value += num
#반복문을 탈출했을때, sum_value+1은 만들 수 없는 수의 최솟값
print(sum_value+1)
7. 연습문제2
2437번: 저울
하나의 양팔 저울을 이용하여 물건의 무게를 측정하려고 한다. 이 저울의 양 팔의 끝에는 물건이나 추를 올려놓는 접시가 달려 있고, 양팔의 길이는 같다. 또한, 저울의 한쪽에는 저울추들만 놓
www.acmicpc.net
사실상 위와 똑같은 문제
하지만 수열의 범위가 길어서 이제는 부분집합을 모두 구하는 완전탐색으로는 불가능하다
8. 풀이
똑같은 문제니까... 똑같이 제출하면 그게 정답이다
from sys import stdin
n = int(stdin.readline())
#수열을 오름차순으로 정렬
s = sorted(map(int,stdin.readline().split()))
#처음에 0~0까지 만들 수 있다
sum_value = 0
#작은 수부터 꺼내서,
for num in s:
#나온 수가 만들 수 있는 수의 최댓값+1보다 크다면,
#만들 수 있는 수의 최댓값+1부터 num-1까지는 만들 수 없는 수이다.
if sum_value+1 < num:
break
#만들 수 있는 수의 최댓값+1이 num이상이라면,
#그러면 나는 0~sum_value+num까지 이제 만들 수 있게 되었다.
sum_value += num
#반복문을 탈출했을때, sum_value+1은 만들 수 없는 수의 최솟값
print(sum_value+1)'알고리즘 > 그리디 알고리즘' 카테고리의 다른 글
| 탐욕적인 사람 되기 -정수 a를 k로 만들기 문제- (0) | 2023.01.05 |
|---|---|
| 탐욕적으로 생각하기 연습 -팩토리얼 분해- (0) | 2023.01.05 |
| 그리디 알고리즘 - 탐욕적으로 생각하게 연습하기1(11508 2+1세일, 1789 수들의 합) (0) | 2022.12.07 |
| 회의실 배정 문제 응용하기 -모든 수업을 가능하게 하는 회의실의 수는- (0) | 2022.10.18 |
| 탐욕 알고리즘 - 회의실 배정문제 해법 - (0) | 2022.09.26 |

